Mathématiques Terminale Spécialité

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Exercices 48 à 65
Exercices transversaux
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les exercices transversaux sont des exercices qui mélangent les notions de plusieurs chapitres. Cette banque d'exercices peut être utilisée indépendamment de la progression suivie en classe : vous pouvez piocher dedans dans l'ordre que vous souhaitez, en fonction de ce que vous voulez travailler.
À partir de l'exercice , chaque exercice est accompagné de la liste des chapitres concernés pour vous permettre de mieux les retrouver. Ces exercices peuvent parfois être, par nature, plus complexes et permettent alors de valider la compréhension des notions et les raisonnements associés.
À partir de l'exercice , chaque exercice est accompagné de la liste des chapitres concernés pour vous permettre de mieux les retrouver. Ces exercices peuvent parfois être, par nature, plus complexes et permettent alors de valider la compréhension des notions et les raisonnements associés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Divers
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
Chapitres • 1. Combinatoire et dénombrement • 2. Vecteurs, droites et plans de l'espace
Soit n un entier naturel supérieur ou égal à 3. On place n points dans l'espace tels que quatre points ne sont jamais coplanaires.
1. Combien de plans différents peut‑on construire à partir de ces points ?
2. Combien, au maximum, existe‑t‑il de droites qui soient des intersections de ces plans ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
Chapitres • 1. Combinatoire et dénombrement • 11. Calcul intégral
Soit n un entier naturel. Pour un entier k, compris entre 0 et n, la k‑ième fonction polynomiale de Bernstein est la fonction \mathrm{B}_{k}^{n} définie, pour tout x \in[0~; 1], par :
1. Montrer que, pour tout entier k compris entre 0 et n et, pour tout x \in[0~; 1], \mathrm{B}_{k}^{n}(x) \geqslant 0.
2. a. Montrer que, pour tout entier k compris entre 0 et n et, pour tout x \in[0~; 1], \mathrm{B}_{k}^{n}(x)=\mathrm{B}_{n-k}^{n}(1-x).
b. Que peut‑on en déduire sur les courbes représentatives des fonctions \mathrm{B}_{k}^{n} et \mathrm{B}_{n-k}^{n} ?
\mathrm{B}_{k}^{n}(x)=\left(\begin{array}{l}n \\ k\end{array}\right) x^{k}(1-x)^{n-k}.
1. Montrer que, pour tout entier k compris entre 0 et n et, pour tout x \in[0~; 1], \mathrm{B}_{k}^{n}(x) \geqslant 0.
2. a. Montrer que, pour tout entier k compris entre 0 et n et, pour tout x \in[0~; 1], \mathrm{B}_{k}^{n}(x)=\mathrm{B}_{n-k}^{n}(1-x).
b. Que peut‑on en déduire sur les courbes représentatives des fonctions \mathrm{B}_{k}^{n} et \mathrm{B}_{n-k}^{n} ?
3. On suppose désormais que k \lt n.
a. À l'aide d'une intégration par parties, montrer que \displaystyle\int_{0}^{1} x^{k}(1-x)^{n-k} \mathrm{d} x=\frac{n-k}{k+1} \displaystyle\int_{0}^{1} x^{k+1}(1-x)^{n-k-1} \mathrm{d} x.
b. En déduire que, pour tout entier k tel que 0 \leqslant k\lt n, \displaystyle\int_{0}^{1} \mathrm{B}_{k}^{n}(x) \mathrm{d} x=\displaystyle\int_{0}^{1} \mathrm{B}_{k+1}^{n}(x) \mathrm{d} x.
c. En déduire que, pour tout entier k tel que 0 \leqslant k\lt n, \displaystyle\int_{0}^{1} \mathrm{B}_{k}^{n}(x) \mathrm{d} x=\frac{1}{n+1}.
4. On suppose que n et k sont distincts et non nuls.
Étudier les variations de la fonction \mathrm{B}_{k}^{n} sur [0~; 1].
a. À l'aide d'une intégration par parties, montrer que \displaystyle\int_{0}^{1} x^{k}(1-x)^{n-k} \mathrm{d} x=\frac{n-k}{k+1} \displaystyle\int_{0}^{1} x^{k+1}(1-x)^{n-k-1} \mathrm{d} x.
b. En déduire que, pour tout entier k tel que 0 \leqslant k\lt n, \displaystyle\int_{0}^{1} \mathrm{B}_{k}^{n}(x) \mathrm{d} x=\displaystyle\int_{0}^{1} \mathrm{B}_{k+1}^{n}(x) \mathrm{d} x.
c. En déduire que, pour tout entier k tel que 0 \leqslant k\lt n, \displaystyle\int_{0}^{1} \mathrm{B}_{k}^{n}(x) \mathrm{d} x=\frac{1}{n+1}.
4. On suppose que n et k sont distincts et non nuls.
Étudier les variations de la fonction \mathrm{B}_{k}^{n} sur [0~; 1].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
Chapitres • 2. Vecteurs, droites et plans de l'espace • 12. Loi binomiale
Partie A
On lance trois fois de suite un dé non truqué à six faces numérotées de 1 à 6. On note x le résultat du premier lancer, y le résultat du deuxième lancer et z le résultat du troisième lancer.
L'espace étant rapporté au repère (\mathrm{O}~;\overrightarrow{i}~,\overrightarrow{j}~,\overrightarrow{k}), on considère les trois points de l'espace \text{I}, \text{J} et \text{K} de coordonnées respectives (x~; 2~; 3), (1~; y~; 3) et (1~; 2~; z).
1. Déterminer la probabilité que les points \text{I}, \text{J} et \text{K} soient confondus.
2. Déterminer la probabilité que seuls les points \text{I} et \text{J} soient confondus.
3. Déterminer la probabilité qu'exactement deux points soient confondus.
4. On suppose dans cette question que \text{I}, \text{J} et \text{K} sont distincts. Déterminer la probabilité que \text{I}, \text{J} et \text{K} ne soient pas alignés.
On lance trois fois de suite un dé non truqué à six faces numérotées de 1 à 6. On note x le résultat du premier lancer, y le résultat du deuxième lancer et z le résultat du troisième lancer.
L'espace étant rapporté au repère (\mathrm{O}~;\overrightarrow{i}~,\overrightarrow{j}~,\overrightarrow{k}), on considère les trois points de l'espace \text{I}, \text{J} et \text{K} de coordonnées respectives (x~; 2~; 3), (1~; y~; 3) et (1~; 2~; z).
1. Déterminer la probabilité que les points \text{I}, \text{J} et \text{K} soient confondus.
2. Déterminer la probabilité que seuls les points \text{I} et \text{J} soient confondus.
3. Déterminer la probabilité qu'exactement deux points soient confondus.
4. On suppose dans cette question que \text{I}, \text{J} et \text{K} sont distincts. Déterminer la probabilité que \text{I}, \text{J} et \text{K} ne soient pas alignés.
Partie B
On considère le jeu qui consiste à lancer trois fois de ce suite le dé et à observer la position des points dans l'espace. Une partie est gagnée lorsque deux points exactement sont confondus. On joue n parties et on appelle \text{X} la variable aléatoire correspondant aux nombres de parties gagnées.
1. Déterminer la loi de probabilité de \text{X}.
2. Dans cette question n = 10.
a. Calculer \mathrm{P}(\mathrm{X}=5).
b. Calculer \mathrm{P}(\mathrm{X}>5).
3. Déterminer la plus petite valeur de n telle que :
On considère le jeu qui consiste à lancer trois fois de ce suite le dé et à observer la position des points dans l'espace. Une partie est gagnée lorsque deux points exactement sont confondus. On joue n parties et on appelle \text{X} la variable aléatoire correspondant aux nombres de parties gagnées.
1. Déterminer la loi de probabilité de \text{X}.
2. Dans cette question n = 10.
a. Calculer \mathrm{P}(\mathrm{X}=5).
b. Calculer \mathrm{P}(\mathrm{X}>5).
3. Déterminer la plus petite valeur de n telle que :
\mathrm{P}(\mathrm{X} \geqslant 1) \geqslant 0{,}999.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
Chapitres • 3. Orthogonalité et distances dans l'espace • 7. Compléments sur la dérivation
On considère un vecteur \overrightarrow{u_{t}} dont les coordonnées sont des fonctions dépendantes du temps t.
On note ce vecteur \vec{u}_{t}\left(\begin{array}{l}x(t) \\ y(t) \\ z(t)\end{array}\right).
On suppose, de plus, que la norme de \overrightarrow{u_{t}} est constante et non nulle.
On note \frac{\mathrm{d} \overrightarrow{u_{t}}}{\mathrm{d} t} le vecteur dérivé de \overrightarrow{u_{t}} : les composantes de \frac{\mathrm{d} \overrightarrow{u_{t}}}{\mathrm{d} t} sont les dérivées respectives de celles de \overrightarrow{u_{t}}.
1. a. On définit la fonction f sur \R par f(t)=\overrightarrow{u_{t}} \cdot \overrightarrow{u_{t}}.
Calculer l'expression de f en fonction de t et démontrer que f est strictement positive sur \R.
b. On définit la fonction g sur \R par g(t)=\sqrt{f(t)}.
Déterminer l'expression de g', fonction dérivée de g.
2. a. Déterminer le lien entre g et la norme de \overrightarrow{u_{t}}.
b. Que peut‑on en déduire pour \overrightarrow{u_{t}} et \frac{\mathrm{d} \overrightarrow{u_{t}}}{\mathrm{d} t} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
Chapitres • 3. Orthogonalité et distances dans l'espace • 4. Suites • 5. Limites de fonctions
On considère trois suites réelles (x_n), (y_n) et (z_n) définies pour tout n \in \N, et on définit la suite de vecteurs (\overrightarrow{u_{n}}) telle que les coordonnées de \overrightarrow{u_{n}} soient \left(\begin{array}{l}x_{n} \\ y_{n} \\ z_{n}\end{array}\right) pour tout n \in \N.
Si les suites (x_n), (y_n) et (z_n) sont convergentes, alors on définit le vecteur \overrightarrow{u} par \vec{u}=\lim\limits_{\substack{n \rightarrow+\infty}} \vec{u}_{n}, dont les coordonnées sont \left(\begin{array}{c}\lim\limits_{\substack{n \rightarrow+\infty}} x_{n} \\ \lim\limits_{\substack{n \rightarrow+\infty}} y_{n} \\ \lim\limits_{\substack{n \rightarrow+\infty}} z_{n}\end{array}\right).
1. Pour tout n \in \N, on pose \overrightarrow{u_{n}} le vecteur de coordonnées \left(\begin{array}{c}\frac{n^{2}}{n^{2}+1} \\ -9+\mathrm{e}^{-n} \\ -360\end{array}\right).
Déterminer les coordonnées de \vec{u}=\lim\limits_{\substack{n \rightarrow+\infty}} \vec{u}_{n}.
2. Pour tout n \in \N, on pose les vecteurs suivants.
- \vec{v}_{n}\left(\begin{array}{c}n^{2} \\ n \\ 1\end{array}\right)
- \overrightarrow{r_{n}}\left(\begin{array}{c}n \mathrm{e}^{-n} \\ \mathrm{e}^{-n} \\ 0\end{array}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
Chapitres • 2. Vecteurs, droites et plans de l'espace • 3. Orthogonalité et distances dans l'espace
L'espace est rapporté à un repère orthonormé (\mathrm{O}~;\overrightarrow{i}~,\overrightarrow{j}~,\overrightarrow{k}).
On considère les points \mathrm{A}(2~; 3~; 1) et \mathrm{B}(-2~; 1~; 3) ainsi que le droite \Delta de représentation paramétrique :
On considère les points \mathrm{A}(2~; 3~; 1) et \mathrm{B}(-2~; 1~; 3) ainsi que le droite \Delta de représentation paramétrique :
\left\{\begin{array}{l}x=t-1 \\ y=2 t+2 \\ z=t\end{array}\right., où t \in \R.
On note \text{I} le milieu de [\mathrm{AB}].
Déterminer, s'il existe, le point \text{J} appartenant à \Delta tel que la distance \text{IJ} soit minimale.
Déterminer, s'il existe, le point \text{J} appartenant à \Delta tel que la distance \text{IJ} soit minimale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
Chapitres • 4. Suites • 9. Fonctions trigonométriques • 11. Calcul intégral
D'après bac S, Polynésie, juin 2018
Dans cet exercice, on s'intéresse au volume d'une ampoule basse consommation. Partie A : Modélisation de la forme de l'ampoule
Le plan est muni d'un repère orthonormé (\mathrm{O}~;\overrightarrow{i}~,\overrightarrow{j}).
On considère les points \mathrm{A}(-1~; 1), \mathrm{B}(0~; 1), \mathrm{C}(4~; 3), \mathrm{D}(7~; 0), \mathrm{E}(4~;-3), \mathrm{F}(0~;-1) et \mathrm{G}(-1~;-1).
On modélise la section de l'ampoule par un plan passant par son axe de révolution à l'aide de la figure ci‑dessous.

On considère les points \mathrm{A}(-1~; 1), \mathrm{B}(0~; 1), \mathrm{C}(4~; 3), \mathrm{D}(7~; 0), \mathrm{E}(4~;-3), \mathrm{F}(0~;-1) et \mathrm{G}(-1~;-1).
On modélise la section de l'ampoule par un plan passant par son axe de révolution à l'aide de la figure ci‑dessous.

La partie de la courbe située au‑dessus de l'axe des abscisses se décompose de la manière suivante :
La partie de la courbe située en‑dessous de l'axe des abscisses est obtenue par symétrie par rapport à l'axe des abscisses.
- la portion située entre les points \text{A} et \text{B} est la représentation graphique de la fonction constante h définie sur l'intervalle [-1~; 0] par h(x)=1 ;
- la portion située entre les points \text{B} et \text{C} est la représentation graphique d'une fonction f définie sur l'intervalle [0~; 4] par f(x)=a+b \sin \left(c+\frac{\pi}{4} x\right), où a, b et c sont des réels non nuls fixés et où le réel c appartient à l'intervalle \left[0~; \frac{\pi}{2}\right] ;
- la portion située entre les points \text{C} et \text{D} est un quart de cercle de diamètre [\mathrm{CE}].
La partie de la courbe située en‑dessous de l'axe des abscisses est obtenue par symétrie par rapport à l'axe des abscisses.
b. On impose que les tangentes aux points \text{B} et \text{C} à la représentation graphique de la fonction f soient parallèles à l'axe des abscisses.
Déterminer la valeur du réel c.
2. Déterminer les réels a et b.
Partie B : Approximation du volume de l'ampoule
Par rotation de la figure précédente autour de l'axe des abscisses, on obtient un modèle de l'ampoule. Afin d'en calculer le volume, on la décompose en trois parties comme illustré ci‑après.

On admet que, pour tout réel x de l'intervalle [0~; 4] :
f(x)=2-\cos \left(\frac{\pi}{4} x\right).
1. Calculer le volume du cylindre de section le rectangle \text{ABFG}.
2. Calculer le volume de la demi‑sphère de section le demi‑disque de diamètre [\mathrm{CE}].
3. Pour approcher le volume du solide de section la zone verte \text{BCEF}, on partage le segment \left[\mathrm{OO}^{\prime}\right] ci‑dessous en n segments de même longueur \frac{4}{n} puis on construit n cylindres de même hauteur \frac{4}{n}.
a. Dans cette question, on choisit n = 5.
Calculer le volume du troisième cylindre, en bleu dans la figure ci‑dessous, et en donner la valeur arrondie à 10^{-2} près.

Calculer le volume du troisième cylindre, en bleu dans la figure ci‑dessous, et en donner la valeur arrondie à 10^{-2} près.

b. Dans cette question, n désigne un entier naturel quelconque non nul. On approche le volume du solide de section \text{BCEF} par la somme des volumes des n cylindres ainsi créés, en choisissant une valeur de n suffisamment grande.
Compléter l'algorithme suivant de sorte qu'à la fin de son exécution, la variable V contienne la somme des volumes des n cylindres créés lorsque l'on saisit n.
Compléter l'algorithme suivant de sorte qu'à la fin de son exécution, la variable V contienne la somme des volumes des n cylindres créés lorsque l'on saisit n.
V = 0 for k in range(...,...) : V = ... return(V)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
Chapitres • 5. Limites de fonctions • 6. Continuité • 11. Calcul intégral
Soit \mathrm{I}=[0~;+\infty[ un intervalle de \R. On appelle densité de probabilité sur \text{I} toute fonction f définie sur \text{I} telle que :
- f est continue et positive sur \text{I} ;
- l'aire du domaine délimité par la courbe \mathcal{C}_f de la fonction f dans un repère orthonormé, l'axe des abscisses et l'axe des ordonnées est égale à 1 unité d'aire.
On définit la fonction f sur [0~;+\infty[ par f(x)=\lambda \mathrm{e}^{-\lambda x}.
a. Montrer que f est continue et positive sur [0~;+\infty[.
b. Soient a > 0 et \mathrm{F}(a) l'aire du domaine délimité par la courbe \mathcal{C}_f, l'axe des abscisses et les droites d'équation x = 0 et x = a.
Montrer que, pour tout a > 0, \mathrm{F}(a)=1-\mathrm{e}^{-\lambda a}.
b. Soient a > 0 et \mathrm{F}(a) l'aire du domaine délimité par la courbe \mathcal{C}_f, l'axe des abscisses et les droites d'équation x = 0 et x = a.
Montrer que, pour tout a > 0, \mathrm{F}(a)=1-\mathrm{e}^{-\lambda a}.
c. Déterminer la limite de \text{F} lorsque a tend vers +\infty.
d. En déduire que f est une densité de probabilité sur [0~;+\infty[.
d. En déduire que f est une densité de probabilité sur [0~;+\infty[.
2. On dit qu'une variable aléatoire \text{X} suit une loi exponentielle de paramètre \lambda, avec \lambda > 0, lorsque sa densité de probabilité est la fonction f.
On a alors : \mathrm{P}(\mathrm{X} \in[a~; b])=\displaystyle\int_{a}^{b} f(x) \mathrm{d} x.
Déterminer, à 10^{-3} près, \mathrm{P}(500 \leqslant \mathrm{X} \leqslant 1~500) lorsque\text{ X} suit la loi exponentielle de paramètre \lambda = 10^{-4}.
On a alors : \mathrm{P}(\mathrm{X} \in[a~; b])=\displaystyle\int_{a}^{b} f(x) \mathrm{d} x.
Déterminer, à 10^{-3} près, \mathrm{P}(500 \leqslant \mathrm{X} \leqslant 1~500) lorsque\text{ X} suit la loi exponentielle de paramètre \lambda = 10^{-4}.
3. Soit g la fonction définie sur [3~;+\infty[ par g(x)=\frac{1}{(x-2)^{2}}.
Montrer que g est une densité de probabilité sur [3~;+\infty[. On pourra s'inspirer de ce qui a été réalisé dans la question 1..
Montrer que g est une densité de probabilité sur [3~;+\infty[. On pourra s'inspirer de ce qui a été réalisé dans la question 1..
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
Chapitres • 6. Continuité • 9. Fonctions trigonométriques
1. Étudier sur \R les variations de la fonction f: x \mapsto x-\cos (x).
2. Montrer que l'équation f(x) = 0 admet une unique solution \alpha, dont on donnera un encadrement d'amplitude 10^{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
Chapitres • 6. Continuité • 9. Fonctions trigonométriques
Soit f la fonction définie pour tout x \in[-1~; 5] par :
f(x)=\frac{\mathrm{e}^{-x}}{2}(\cos (x)+\sin (x)-2 x+1).
1. Déterminer l'expression f'(x) pour x \in[-1~; 5].
2. Soit g la fonction définie pour tout x \in[-1~; 5] par :
g(x)=2 x-3-2 \sin (x).
a. Démontrer qu'il existe un unique réel \alpha \in[2{,}2~; 2{,}3] tel que g(\alpha)=0.b. En déduire le tableau de variations de f sur [-1~; 5].
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
Chapitres • 6. Continuité • 9. Fonctions trigonométriques • 11. Calcul intégral • 14. Loi des grands nombres
Soit \mathrm{I}=[a~; b] un intervalle de \R.
On appelle densité de probabilité sur \text{I} toute fonction f définie sur \text{I} telle que :
- f est continue et positive sur \text{I} ;
- l'aire du domaine délimité par la courbe \mathcal{C}_f de la fonction f dans un repère orthonormé, l'axe des abscisses et les droites d'équations respectives x = a et x = b est égale à 1 unité d'aire.
On dit que \text{X} est une variable aléatoire continue de densité f lorsque, pour tous k et k' dans [a~; b] \mathrm{P}\left(k \leqslant \mathrm{X} \leqslant k^{\prime}\right)=\displaystyle\int_{k}^{k^{\prime}} f(x) \mathrm{d} x.
On définit alors l'espérance d'une loi continue sur [a~; b] de densité f par :
\mathrm{E}(\mathrm{X})=\displaystyle\int_{a}^{b} x f(x) \mathrm{d} x et \mathrm{E}\left(\mathrm{X}^{2}\right)=\displaystyle\int_{a}^{b} x^{2} f(x) \mathrm{d} x.
1. Montrer que la fonction f: x \mapsto \cos (x) est une densité sur \left[0~; \frac{\pi}{2}\right].
2. Calculer l'espérance de \text{X} de densité f sur \left[0~; \frac{\pi}{2}\right].
2. Calculer l'espérance de \text{X} de densité f sur \left[0~; \frac{\pi}{2}\right].
3. On rappelle la formule de König‑Huygens :
4. On admet que l'inégalité de Bienaymé‑Tchebychev est valable pour les lois continues.
Majorer alors \mathrm{P}\left(|\mathrm{X}-\mathrm{E}(\mathrm{X})| \geqslant \frac{1}{2}\right).
\mathrm{V}(\mathrm{X})=\mathrm{E}\left(\mathrm{X}^{2}\right)-(\mathrm{E}(\mathrm{X}))^{2}.
Calculer alors la variance de \text{X}.4. On admet que l'inégalité de Bienaymé‑Tchebychev est valable pour les lois continues.
Majorer alors \mathrm{P}\left(|\mathrm{X}-\mathrm{E}(\mathrm{X})| \geqslant \frac{1}{2}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
Chapitres • 5. Limites de fonctions • 11. Calcul intégral
1. On considère un réel \mathrm{A} > 0 et on note \mathrm{I}_{\mathrm{A}} l'intégrale \mathrm{I}_{\mathrm{A}}=\displaystyle\int_{1}^{\mathrm{A}} x \mathrm{e}^{-x^{2}} \mathrm{d} x.
a. Calculer \mathrm{I}_{\mathrm{A}} en fonction de \text{A}.
b. En déduire \lim\limits_{\substack{\mathrm{A} \rightarrow+\infty}} \mathrm{I}_{\mathrm{A}}.
Le résultat obtenu se note \displaystyle\int_{1}^{+\infty} x \mathrm{e}^{-x^{2}} \mathrm{d} x. On parle d'intégrale impropre.
2. De la même manière, démontrer que \displaystyle\int_{3}^{+\infty} \frac{x}{\left(x^{2}-5\right)^{2}} \mathrm{d} x=\frac{1}{8}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
Chapitres • 3. Orthogonalité et distances dans l'espace • 9. Fonctions trigonométriques
Déterminer l'ensemble des réels a et b appartenant à l'intervalle [-\pi~; \pi] de sorte que, dans un repère orthonormé de l'espace, le plan \mathcal{P}_{1}: \cos (a) x+\sin (a) y+z=1 soit perpendiculaire à la fois au plan \mathcal{P}_{2}: \cos (2 b) x+\sin (2 b) y+0{,}5 z=2 et au plan \mathcal{P}_{3}: \sin (2 b) x+\cos (2 b) y-0{,}5 z=3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
Chapitres • 7. Compléments sur la dérivation • 11. Calcul intégral
D'après bac ES, Antilles-Guyane, juin 2019
On considère la fonction f définie sur l'intervalle [-10~; 5] par f(x)=(x-5) \mathrm{e}^{0{,}2 x}+5 et on note \mathcal{C} sa courbe représentative dans un repère orthogonal.
1. On note f' la fonction dérivée de f sur [-10~; 5].
a. Montrer que, pour tout x \in[-10~; 5], f^{\prime}(x)=0{,}2 x \mathrm{e}^{0{,}2 x}.
b. Dresser le tableau de variations de f sur [-10~; 5].
c. Déterminer la valeur exacte du coefficient directeur de la tangente \text{T} à \mathcal{C} au point \text{A} d'abscisse -5.
a. Montrer que, pour tout x \in[-10~; 5], f^{\prime}(x)=0{,}2 x \mathrm{e}^{0{,}2 x}.
b. Dresser le tableau de variations de f sur [-10~; 5].
Cliquez pour accéder à une zone de dessin
c. Déterminer la valeur exacte du coefficient directeur de la tangente \text{T} à \mathcal{C} au point \text{A} d'abscisse -5.
2. Un logiciel de calcul formel donne les résultats suivants.

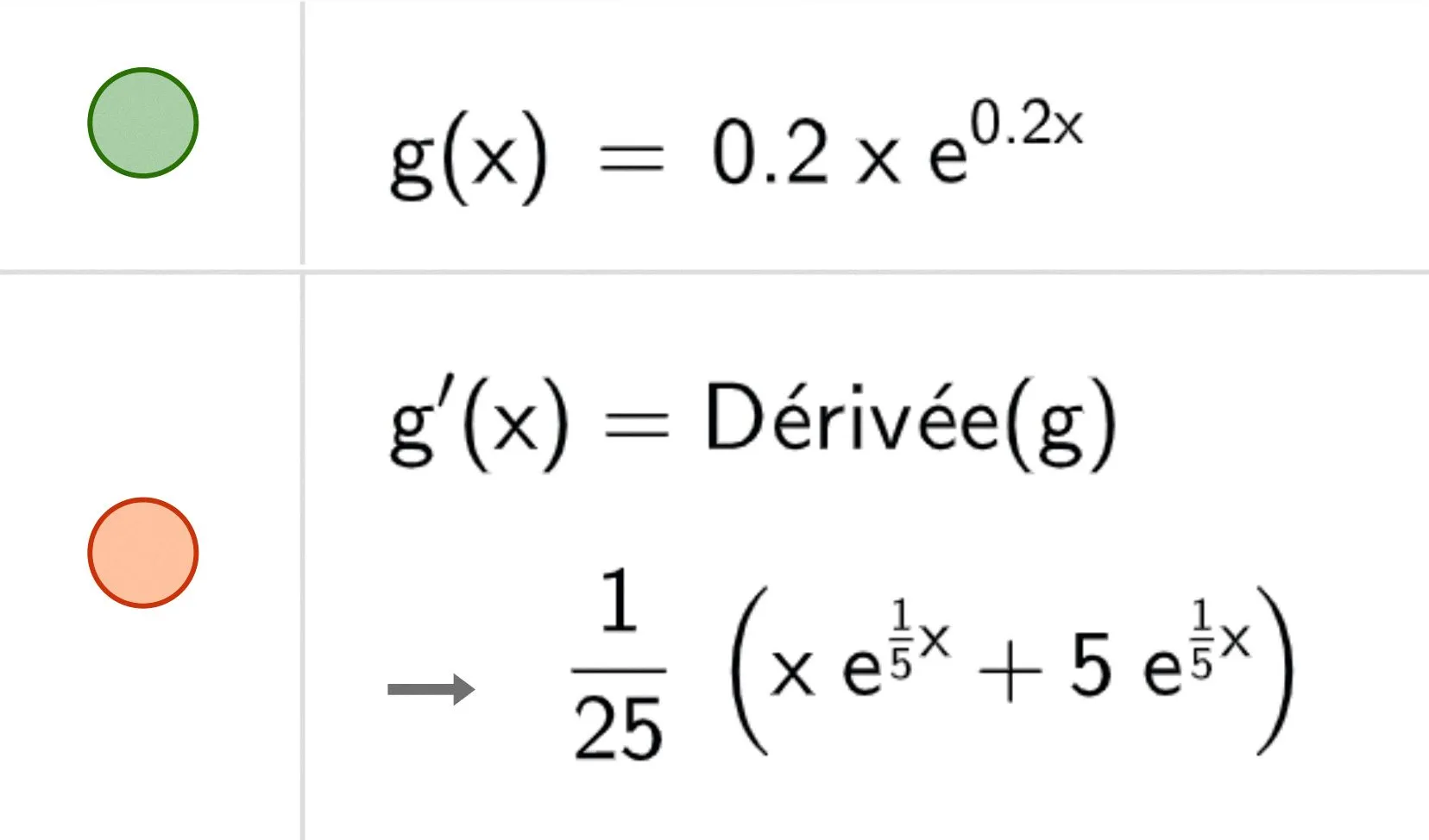
a. En utilisant ces résultats, justifier que la dérivée seconde de f, notée f'', est définie par f^{\prime \prime}(x)=(0{,}2+0{,}04 x) \mathrm{e}^{0{,}2 x}.
b. Étudier la convexité de la fonction f sur [-10~; 5].
3. On définit la fonction \text{F} sur [-10~; 5] par :
b. Calculer la valeur exacte de \mathrm{I}=\displaystyle\int_{0}^{5} f(x) \mathrm{d} x.
c. Déterminer l'aire du domaine délimité par la courbe \mathcal{C} et les trois droites d'équations respectives x = 0, x = 5 et y = x. On donnera le résultat en unité d'aire, arrondi à 10^{-2} près.

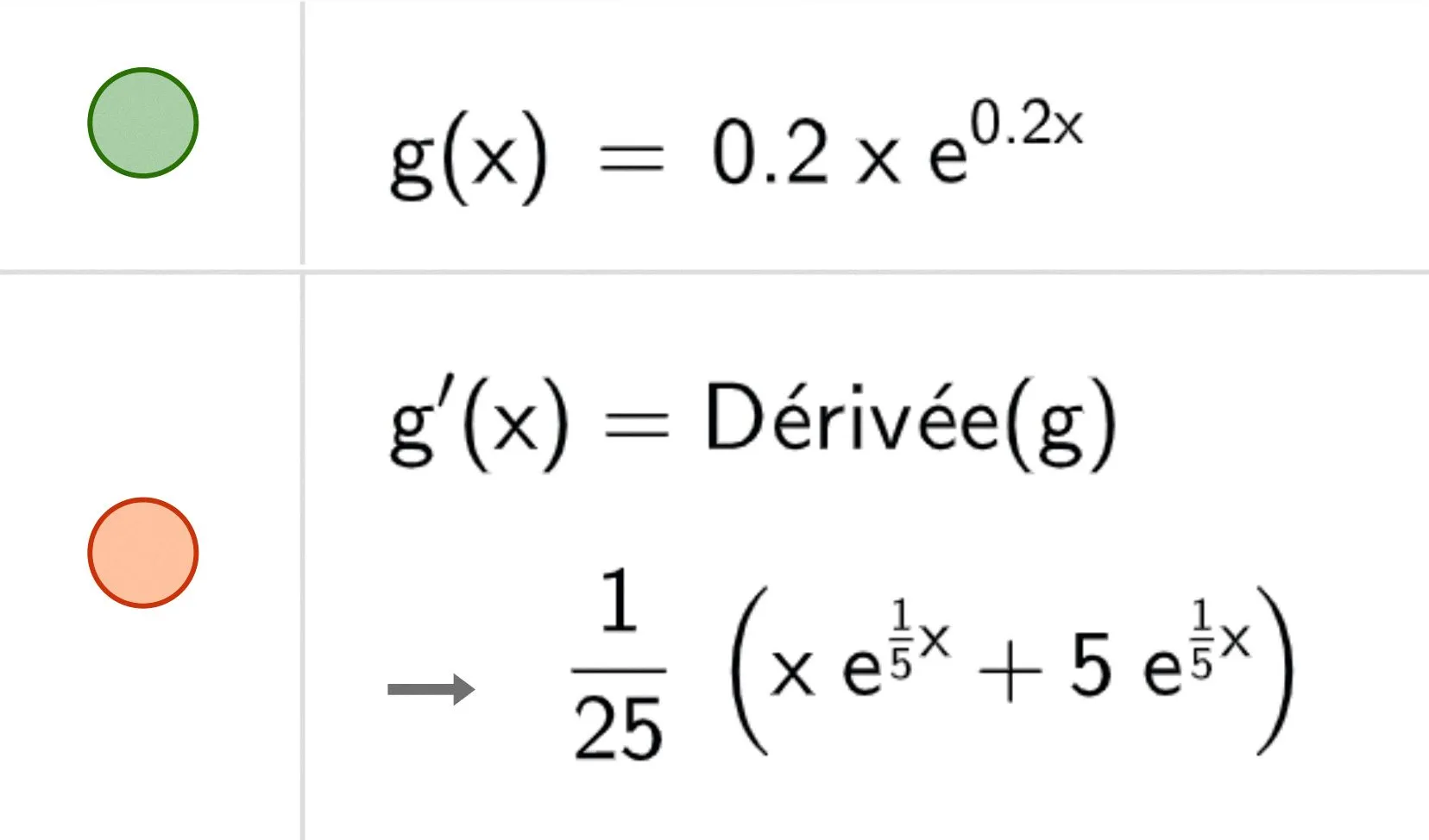
a. En utilisant ces résultats, justifier que la dérivée seconde de f, notée f'', est définie par f^{\prime \prime}(x)=(0{,}2+0{,}04 x) \mathrm{e}^{0{,}2 x}.
b. Étudier la convexité de la fonction f sur [-10~; 5].
3. On définit la fonction \text{F} sur [-10~; 5] par :
\mathrm{F}(x)=(5 x-50) \mathrm{e}^{0{,}2 x}+5 x.
a. Démontrer que \text{F} est une primitive de f sur [-10~; 5].b. Calculer la valeur exacte de \mathrm{I}=\displaystyle\int_{0}^{5} f(x) \mathrm{d} x.
c. Déterminer l'aire du domaine délimité par la courbe \mathcal{C} et les trois droites d'équations respectives x = 0, x = 5 et y = x. On donnera le résultat en unité d'aire, arrondi à 10^{-2} près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
Chapitres • 4. Suites • 5. Limites de fonctions • 9. Fonctions trigonométriques
Partie A
Soit f la fonction définie sur [0~;+\infty[ par :
f(x)=x^{2}-1-\cos ^{2}(x).
1. Déterminer \lim\limits_{\substack{x \rightarrow+\infty}} f(x).
2. On admet que pour tout réel x :
2. On admet que pour tout réel x :
\sin (2 x)=2 \cos (x) \sin (x).
Montrer que, pour tout réel x, f^{\prime}(x)=2 x+\sin (2 x).
3. a. Calculer f'(0) et démontrer que, pour tout x > 0, f^{\prime}(x)>0.
b. En déduire les variations de f sur [0~;+\infty[.
b. En déduire les variations de f sur [0~;+\infty[.
4. Démontrer que l'équation f(x) = 0 admet une unique solution dans [0~;+\infty[. On note \alpha cette solution.
5. À l'aide de la calculatrice, encadrer \alpha à 10^{-2} près.
Soit (u_n), la suite définie par u_0=10 et, pour tout entier naturel n, u_{n+1}=\sqrt{1+\cos ^{2}\left(u_{n}\right)}.
1. Montrer que, pour tout n \geqslant 2, on a 1 \lt u_{n} \lt 1{,}2.
2. a. Justifier que la suite (u_n) ne peut ni diverger vers +\infty, ni vers -\infty.
b. Justifier que si (u_n) converge vers un réel \ell, alors nécessairement \ell \in[1~; 1{,}2].
À partir des deux premières parties, montrer que si (u_n) converge vers un réel \ell, alors \ell = \alpha.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
Chapitres • 1. Combinatoire et dénombrement • 12. Loi binomiale
Soient a un nombre réel strictement positif et k un entier naturel fixé. Soit \mathrm{X}_n une variable aléatoire suivant une loi binomiale \mathcal{B}(n~; p) telle que np = a.
Par définition, on dit qu'une variable aléatoire \text{Y} suit une loi de Poisson de paramètre a lorsque :
\mathrm{P}(\mathrm{Y}=k)=\frac{a^{k}}{k !} \mathrm{e}^{-a}.
On souhaite montrer qu'une loi binomiale converge vers une loi de Poisson.
1. Montrer que, pour tous entiers naturels n et k \leqslant n :
2. En factorisant astucieusement chacun des facteurs du numérateur, montrer que, pour tout entier naturel n > 0 :
3. En utilisant np = a, réécrire l'égalité précédente sans utiliser p.
4. Déterminer \lim\limits_{\substack{n \rightarrow+\infty}}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \ldots\left(1-\frac{k-1}{n}\right).
\mathrm{P}\left(\mathrm{X}_{n}=k\right)=\frac{n(n-1)(n-2) \ldots(n-k+1)}{k !} p^{k}(1-p)^{n-k}.
2. En factorisant astucieusement chacun des facteurs du numérateur, montrer que, pour tout entier naturel n > 0 :
\mathrm{P}\left(\mathrm{X}_{n}=k\right)=\frac{(n p)^{k}}{k !}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \ldots\left(1-\frac{k-1}{n}\right)(1-p)^{n-k}.
3. En utilisant np = a, réécrire l'égalité précédente sans utiliser p.
4. Déterminer \lim\limits_{\substack{n \rightarrow+\infty}}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \ldots\left(1-\frac{k-1}{n}\right).
5. a. Déterminer \lim\limits_{\substack{n \rightarrow+\infty}}\left(1-\frac{a}{n}\right)^{-k}.
b. Déterminer \lim\limits_{\substack{n \rightarrow+\infty}}\left(1-\frac{a}{n}\right)^{n}.
6. Après avoir remarqué que :
b. Déterminer \lim\limits_{\substack{n \rightarrow+\infty}}\left(1-\frac{a}{n}\right)^{n}.
6. Après avoir remarqué que :
\left(1-\frac{a}{n}\right)^{n-k}=\left(1-\frac{a}{n}\right)^{n}\left(1-\frac{a}{n}\right)^{-k},
déterminer \lim\limits_{\substack{n \rightarrow+\infty}} \mathrm{P}\left(\mathrm{X}_{n}=k\right) et conclure.Remarque
En pratique, on applique cette approximation dès que n \geqslant 50 et p \lt 0{,}1.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problèmes ouverts
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
Déterminer, en justifiant, le nombre exact de solutions de l'équation (\ln (x))^{2}=\ln \left(x^{2}\right) sur ]0~;+\infty[.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
Rachid, artiste, souhaite peindre un cœur sur un mur. Il utilise, dans un repère orthonormal d'unité 2 mètres, les fonctions f et g définies sur [-\pi~; \pi] par f(x)=\sin (|x|) et g(x)=\frac{5}{\pi}|x|-5.
Déterminer le nombre de pots de peinture nécessaire à Rachid, sachant que deux couches seront appliquées et qu'un pot de deux litres permet de recouvrir 24 m2.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
