Chapitre 6
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44 La lumière parcourt 300 000 km en une seconde
✔ Je modélise une situation à l'aide d'un schéma, d'un tableau ou d'un arbre
✔ Je structure mon raisonnement
À lʼaide des données du tableau ci-dessous, déterminez combien de secondes il faut à la lumière pour atteindre les planètes suivantes en partant du Soleil.
✔ Je structure mon raisonnement
| Planète | Distance au Soleil (millions de km) |
| Mercure | 60 |
| Vénus | 108 |
| Terre | 150 |
| Mars | 228 |
À lʼaide des données du tableau ci-dessous, déterminez combien de secondes il faut à la lumière pour atteindre les planètes suivantes en partant du Soleil.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Quand des grandeurs sont proportionnelles, il est possible de trouver les valeurs manquantes en complétant un tableau de proportionnalité.
Corrigé 1
- La distance d (en km) parcourue par la lumière dépend du temps t (en secondes) et sʼexprime par la formule d = 300\:000\:t. Si on convertit d en millions de km, on obtient alors la formule d = 0\text{,}3\:t. d et t sont donc proportionnels et le coefficient multiplicateur vaut 0\text{,}3.
- Il ne reste plus quʼà construire et compléter un tableau de proportionnalité.
Planète Me V T Ma Temps pour atteindre la planète (s) 1 200 360 00 760 \times 0,3
\downarrowDistance au Soleil (millions de km) 0,3 60 108 150 228
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Quand les données recherchées sont proportionnelles à des valeurs connues, il est possible dʼutiliser une représentation graphique. Une fois tracée la droite représentant la relation de proportionnalité, une simple lecture graphique donnera toutes les valeurs recherchées.
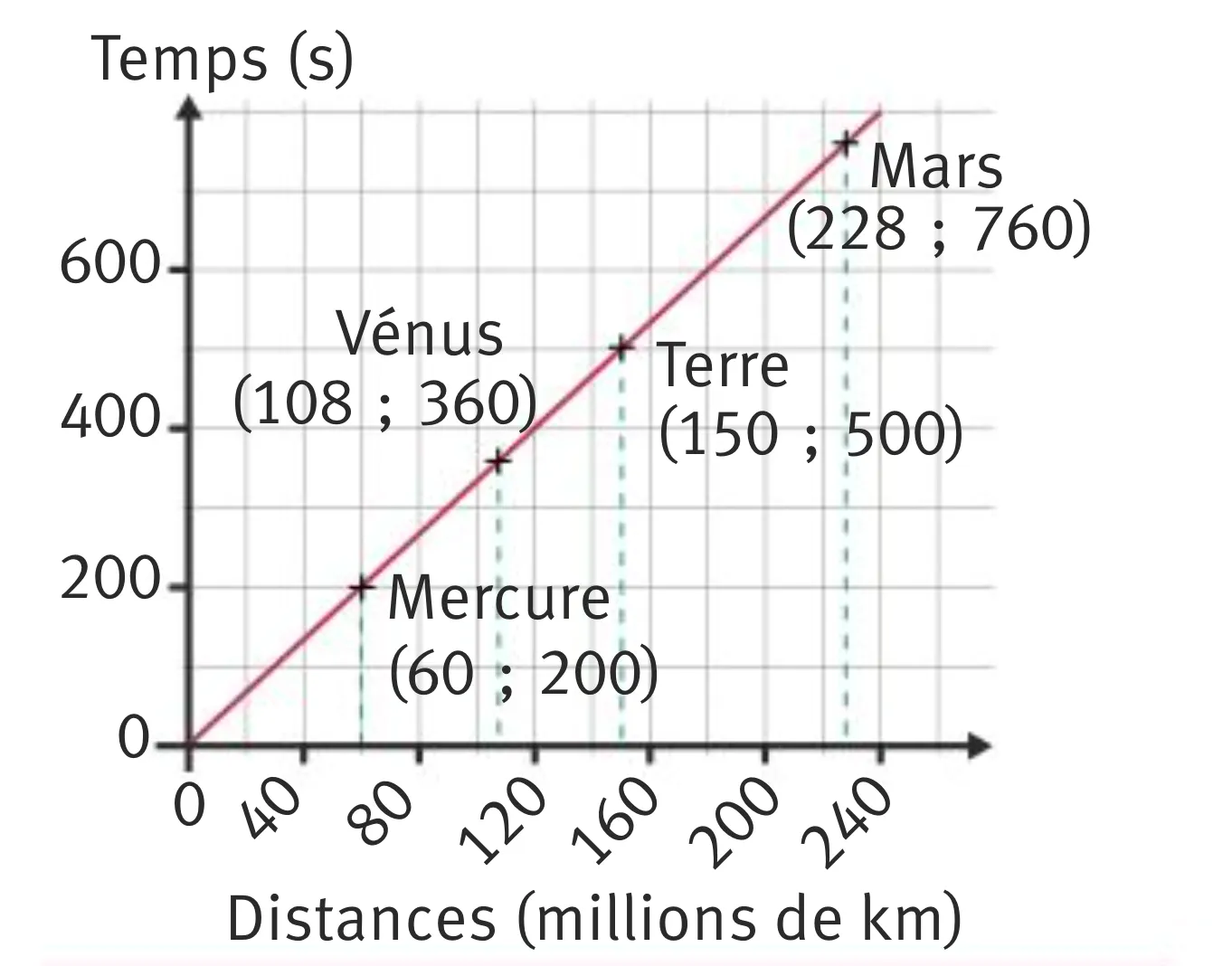
Corrigé 2
- De la même manière que dans le Corrigé 1, on montre que la distance d parcourue par la lumière est proportionnelle au temps t avec la formule d = 0\text{,}3\:t.
- On construit un repère dans lequel on place en abscisse la distance parcourue en millions de km et en ordonnée le temps de parcours en secondes. Il suffi t alors de placer le point de référence dʼabscisse 0,3 et dʼordonnée 1, puis de tracer la droite passant par ce point et lʼorigine du repère. Tous les points recherchés se situent sur cette droite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
