Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 7
Activité A
Pylônes du mont Aigoual
✔ Représenter, dans l'espace muni d'un repère orthonormé, un vecteur dont les coordonnées sont données.
✔ Déterminer graphiquement les coordonnées d'un vecteur.
✔ Calculer la norme d'un vecteur dans l'espace muni d'un repère orthonormé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour assurer la rigidité des pylônes du mont Aigoual, situé dans le sud du Massif central, des haubans ont été installés. Un hauban est un câble en acier ancré au niveau du sol et relié au pylône permettant de consolider la structure. Les pylônes de télécommunications ont une hauteur totale de 40 m. Les haubans sont fixés sur le pylône à 29 m du sol. Pour connaître la longueur des haubans, on a modélisé un pylône dans un repère orthonormé dont l᾽unité graphique est le mètre.
Les fixations des haubans au niveau du sol sont représentées par les points : \mathrm{A}(0 \: ; 0 \: ; 0), \mathrm{B}(40 \: ; 0 \: ; 0), \mathrm{C}(40 \: ; 40 \: ; 0) et \mathrm{D}(0 \: ; 40 \: ; 0).
Les fixations des haubans au niveau du sol sont représentées par les points : \mathrm{A}(0 \: ; 0 \: ; 0), \mathrm{B}(40 \: ; 0 \: ; 0), \mathrm{C}(40 \: ; 40 \: ; 0) et \mathrm{D}(0 \: ; 40 \: ; 0).
Problématique
Quelle est la longueur totale de câble nécessaire pour un pylône du mont Aigoual ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1S'approprier
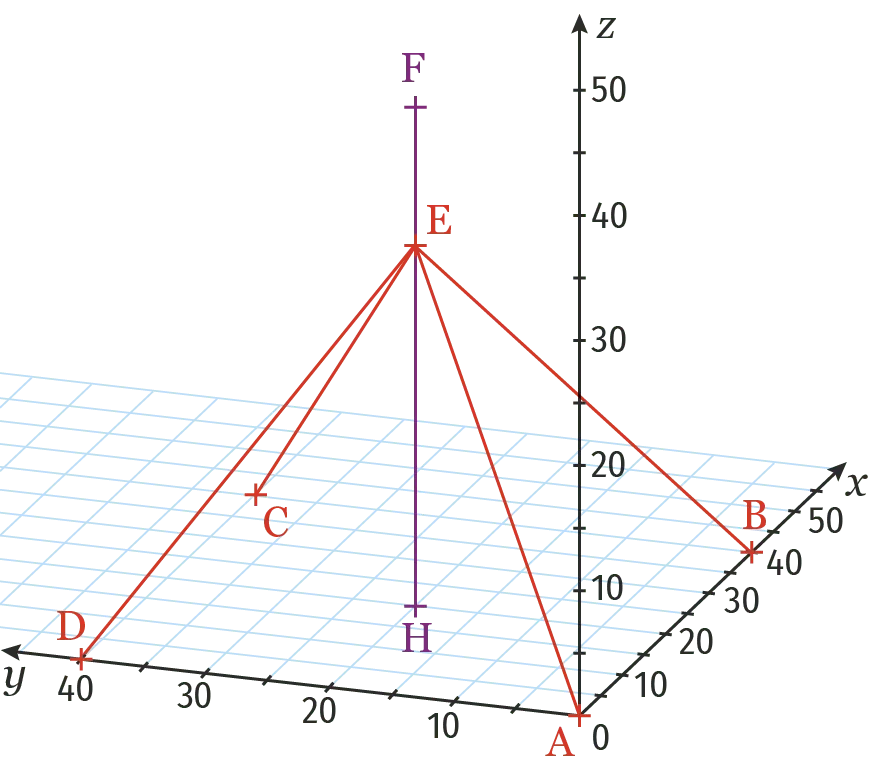
En s᾽aidant du repère ci-dessous et des données de l᾽énoncé, donner les coordonnées des points suivants : \text{E}, le point d᾽attache des haubans, \text{F}, le sommet du pylône et \text{H}, le point de base du pylône.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Analyser/Raisonner
Dans un repère orthonormé de l'espace, si \mathrm{A}\left(x_{\mathrm{A}} ; y_{\mathrm{A}} ; z_{\mathrm{A}}\right) et \mathrm{B}\left(x_{\mathrm{B}} ; y_{\mathrm{B}} ; z_{\mathrm{B}}\right), alors les coordonnées du vecteur \overrightarrow{\mathrm{AB}} sont \overrightarrow{\mathrm{AB}}\left(\begin{array}{c}
x_{\mathrm{B}}-x_{\mathrm{A}} \\
y_{\mathrm{B}}-y_{\mathrm{A}} \\
z_{\mathrm{B}}-z_{\mathrm{A}}
\end{array}\right).
Déterminer les coordonnées des vecteurs \overrightarrow{\mathrm{EA}}, \overrightarrow{\mathrm{EB}}, \overrightarrow{\mathrm{EC}} et \overrightarrow{\mathrm{ED}} symbolisant l'action des haubans sur le pylône.
Déterminer les coordonnées des vecteurs \overrightarrow{\mathrm{EA}}, \overrightarrow{\mathrm{EB}}, \overrightarrow{\mathrm{EC}} et \overrightarrow{\mathrm{ED}} symbolisant l'action des haubans sur le pylône.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Réaliser
Dans un repère orthonormé de l'espace, la norme du vecteur \overrightarrow{\mathrm{AB}} s'obtient de la manière suivante : {\|\overrightarrow{\mathrm{AB}}\|=\sqrt{\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^{2}+\left(z_{\mathrm{B}}-z_{\mathrm{A}}\right)^{2}}}.
Calculer, à 0,01 m près, les longueurs des quatre haubans \text{EA}, \text{EB}, \text{EC} et \text{ED}.
Calculer, à 0,01 m près, les longueurs des quatre haubans \text{EA}, \text{EB}, \text{EC} et \text{ED}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Communiquer
Répondre à la problématique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Valider
Vérifier les longueurs obtenues.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans un repère orthonormé (\mathrm{O} \: ; \vec{i}, \vec{j}, \vec{k}) de l'espace, on considère les points \mathrm{A}\left(x_{\mathrm{A}} ; y_{\mathrm{A}} ; z_{\mathrm{A}}\right) et \mathrm{B}\left(x_{\mathrm{B}} ; y_{\mathrm{B}} ; z_{\mathrm{B}}\right).
- Les coordonnées du vecteur \overrightarrow{\mathrm{AB}} sont \overrightarrow{\mathrm{AB}}\left(\begin{array}{c} x_{\mathrm{B}}-x_{\mathrm{A}} \\ y_{\mathrm{B}}-y_{\mathrm{A}} \\ z_{\mathrm{B}}-z_{\mathrm{A}} \end{array}\right).
- La norme du vecteur \overrightarrow{\mathrm{AB}} est : {\|\overrightarrow{\mathrm{AB}}\|=\sqrt{\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^{2}+\left(z_{\mathrm{B}}-z_{\mathrm{A}}\right)^{2}}}.
Pour s᾽entraîner : et
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah