Mathématiques 3e - Cahier d'exercices - 2021
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Brevet
Dossier brevet
Nombres et calculs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1[D'après brevet, Nouvelle-Calédonie, décembre 2020]
durée : 15 min ❯ Chapitres ,
On donne les deux programmes de calcul suivants.
Programme A
\boxed{ \begin{array} { r|l } 1 & \text{Choisir un nombre} \\ 2 & \text{Soustraire 5 à ce nombre} \\ 3 & \text{Multiplier le résultat par le nombre de départ} \\ \end{array} }
Programme B
\boxed{ \begin{array} { r|l } 1 & \text{Choisir un nombre} \\ 2 & \text{Mettre ce nombre au carré} \\ 3 & \text{Soustraire 4 au résultat} \\ \end{array} }
1. Alice choisit le nombre 4 et applique le programme A. Montrer qu'elle obtiendra -4 .
2. Lucie choisit le nombre -3 et applique le programme B. Quel résultat va-t-elle obtenir ?
3. Tom souhaite trouver un nombre pour lequel les deux programmes de calculs donneront le même résultat. Il choisit x comme nombre de départ pour les deux programmes. Montrer que le résultat du programme A peut s'écrire x^{2}-5 x.
4. Exprimer en fonction de x le résultat obtenu avec le programme \mathrm{B}.
5. Quel est le nombre que Tom cherche ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2
[D'après brevet, Antilles-Guyane, septembre 2020]
durée : 15 min ❯ Chapitres ,
Cet exercice est un questionnaire à choix multiple (QCM). Pour chacune des questions, quatre réponses sont proposées, une seule d'entre elles est exacte. Justifier les réponses.
1. Lorsque x est égal à -4, x^{2}+3 x+4 est égal à :
2. \frac{1}{3}+\frac{1}{4}=
3. La notation scientifique de \text{1 500 000 000} est :
4. (x-2)(x+2)=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3
[D'après brevet, Asie, juin 2018]
durée : 10 min ❯ Chapitre
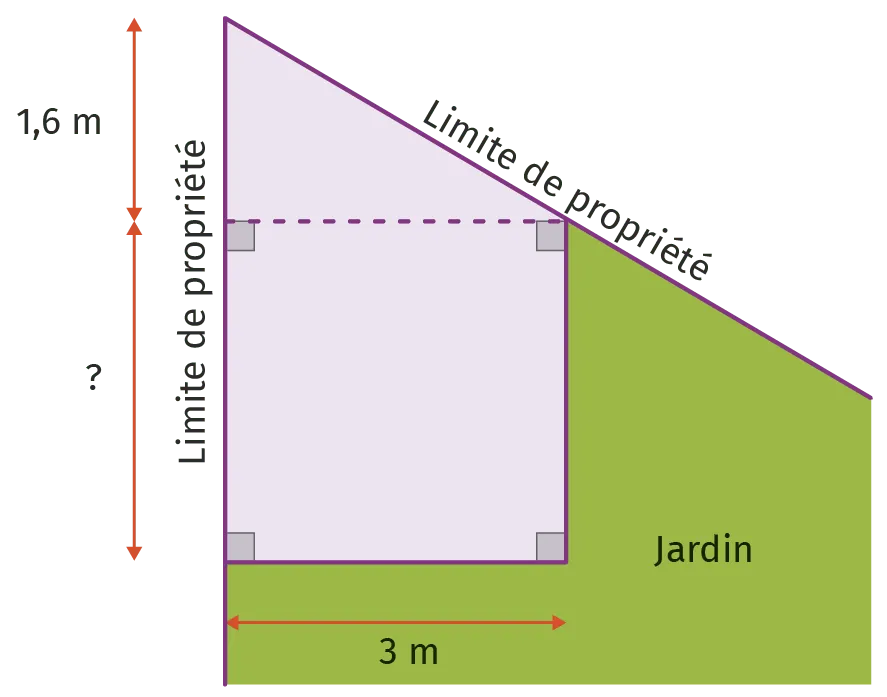
Paul veut construire un garage dans le fond de son jardin. Sur le sch�éma ci-contre, la partie violette représente le garage positionné en limite de propriété. Les longueurs indiquées (1{,}6 \mathrm{~m} et 3 \mathrm{~m} ) sont imposées. La longueur marquée par un point d'interrogation est variable.
Sachant que la surface du garage ne doit pas dépasser 20 \mathrm{~m}^{2}, quelle valeur maximale peut-il choisir pour cette longueur variable ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4
[D'après brevet, Nouvelle-Calédonie, décembre 2020]
durée : 15 min ❯ Chapitre
1. Justifier que le nombre 102 est divisible par 3 .
2. La décomposition en un produit de facteurs premiers de 85 est 85=5 \times 17. Décomposer 102 en un produit de facteurs premiers.
3. Donner trois diviseurs non premiers du nombre 102 .
4. Un libraire dispose d'une feuille cartonnée de 85 \mathrm{~cm} sur 102 \mathrm{~cm}. Il souhaite découper dans celle-ci, en utilisant toute la feuille, des étiquettes carrées. Les côtés de ces étiquettes ont tous la même mesure.
Les étiquettes peuvent-elles avoir 34 \mathrm{~cm} de côté ? Justifier.
5. Le libraire découpe des étiquettes de 17 \mathrm{~cm} de côté. Combien d'étiquettes pourra-t-il découper ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6
[D'après brevet, Centres étrangers, juin 2019]
durée : 15 min ❯ Chapitres ,
Une famille désire acheter, pour les enfants, une piscine cylindrique hors sol équipée d'une pompe électrique. Elle compte l'utiliser cet été, du mois de juin au mois de septembre inclus. Elle dispose d'un budget de 200 \:€. À l'aide des documents suivants, dire si le budget de cette famille est suffisant pour l'achat de cette piscine et ses frais de fonctionnement.
Document 1


Caractéristiques techniques
• Hauteur de l'eau : \text{65 cm}.
• Consommation électrique moyenne
de la pompe : \text{3,42 kWh} par jour.
• Prix (piscine + pompe) : \text{80 €}.
Document 2
Prix d'un \text{kWh} : 0{,}15 €. Le \text{kWh} (kilowatt-heure) est l'unité de mesure de l'énergie électrique.
Document 3
Prix d'un \mathrm{m}^{3} d'eau : 2{,}03 €.
Document 4
Le volume d'un cylindre est donné par la formule \mathrm{V}=\pi \times r^{2} \times h, où r est le rayon du cylindre et h sa hauteur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7
[D'après brevet, Nouvelle-Calédonie, décembre 2017]
durée : 10 min ❯ Chapitre
- AUREL : Belle pêche ! Combien de poissons et de coquillages vas-tu pouvoir vendre au marché ?
- ANTOINE : En tout, je vais pouvoir vendre au marché 30 poissons et 500 coquillages.
Antoine est un pêcheur professionnel. Il veut vendre des paniers contenant des coquillages et des poissons. Il souhaite concevoir le plus grand nombre possible de paniers identiques. Enfin, il voudrait qu'il ne reste aucun coquillage et aucun poisson dans son congélateur.
1. Combien de paniers Antoine pourra t-il concevoir au maximum ? Justifier.
2. Quelle sera la composition de chaque panier ? Justifier.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
