Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 8
Cours 2
Étude des fonctions trigonométriques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADérivées
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Si f est la fonction cosinus et g la fonction sinus, alors f et g sont dérivables sur \mathbb{R} et, pour tout x \in \mathbb{R},f'(x)=-\sin (x) et g'(x)=\cos (x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Soient a et b deux réels quelconques. En notant f : x \mapsto \cos (a x+b) et g : x \mapsto \sin (a x+b), alors f et g sont dérivables sur \mathbb{R} et, pour tout x \in \mathbb{R}, f'(x)=-a \sin (a x+b) et g'(x)=a \cos (a x+b).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Pour toute fonction h dérivable et pour tous réels a et b , on sait que la dérivée de x \mapsto h(a x+b) est x \mapsto a h'(a x+b).
Donc, pour tout réel x, f'(x)=-a \sin (a x+b) et g'(x)=a \cos (a x+b).
Donc, pour tout réel x, f'(x)=-a \sin (a x+b) et g'(x)=a \cos (a x+b).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Voir le cours de la
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Soit la fonction f définie par f(x)=\cos (4 x-1).
On a donc f'(x)=-4 \sin (4 x-1).
On a donc f'(x)=-4 \sin (4 x-1).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Calculer la dérivée des fonctions suivantes.
1. f : x \mapsto \cos (x)+\sin (x)
2. g : x \mapsto \sin (3 x+12)
3. h : x \mapsto \cos (-2 x-3)
1. f : x \mapsto \cos (x)+\sin (x)
2. g : x \mapsto \sin (3 x+12)
3. h : x \mapsto \cos (-2 x-3)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. La fonction f est dérivable sur \mathbb{R} en tant que somme de fonctions dérivables sur \mathbb{R}. Pour tout x \in \mathbb{R}, on a : f'(x)=-\sin (x)+\cos (x).
2. La fonction g est la composée d'une fonction affine avec la fonction sinus. Elle s'écrit sous la forme \sin (a x+b) avec a=3 et b=12 : elle est donc dérivable sur \mathbb{R} et, pour tout x \in \mathbb{R}, g'(x)=3 \cos (3 x+12).
3. La fonction h est la composée d'une fonction affine avec la fonction cosinus. Elle s'écrit sous la forme \cos (a x+b) avec a=-2 et b=-3 : elle est donc dérivable sur \mathbb{R} et, pour tout x \in \mathbb{R}, h'(x)=-(-2) \times \sin (-2 x-3)=2 \sin (-2 x-3).
2. La fonction g est la composée d'une fonction affine avec la fonction sinus. Elle s'écrit sous la forme \sin (a x+b) avec a=3 et b=12 : elle est donc dérivable sur \mathbb{R} et, pour tout x \in \mathbb{R}, g'(x)=3 \cos (3 x+12).
3. La fonction h est la composée d'une fonction affine avec la fonction cosinus. Elle s'écrit sous la forme \cos (a x+b) avec a=-2 et b=-3 : elle est donc dérivable sur \mathbb{R} et, pour tout x \in \mathbb{R}, h'(x)=-(-2) \times \sin (-2 x-3)=2 \sin (-2 x-3).
Pour s'entraîner
exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Il est primordial de préciser sur quel intervalle on a le droit de dériver.
- On applique correctement la formule en identifiant les coefficients a et b .
- Il faut évidemment faire attention aux signes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BTableaux de signes et variations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
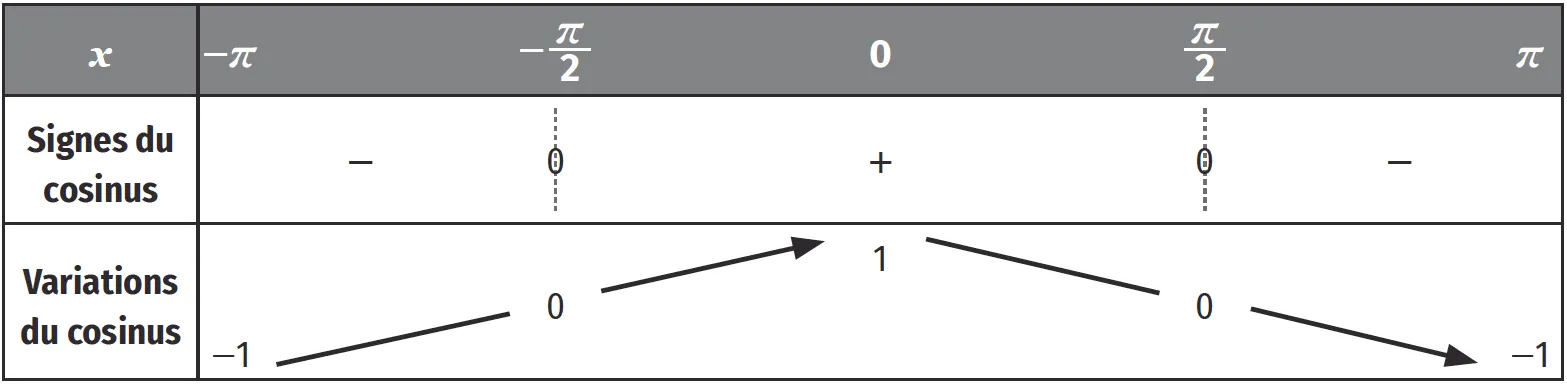
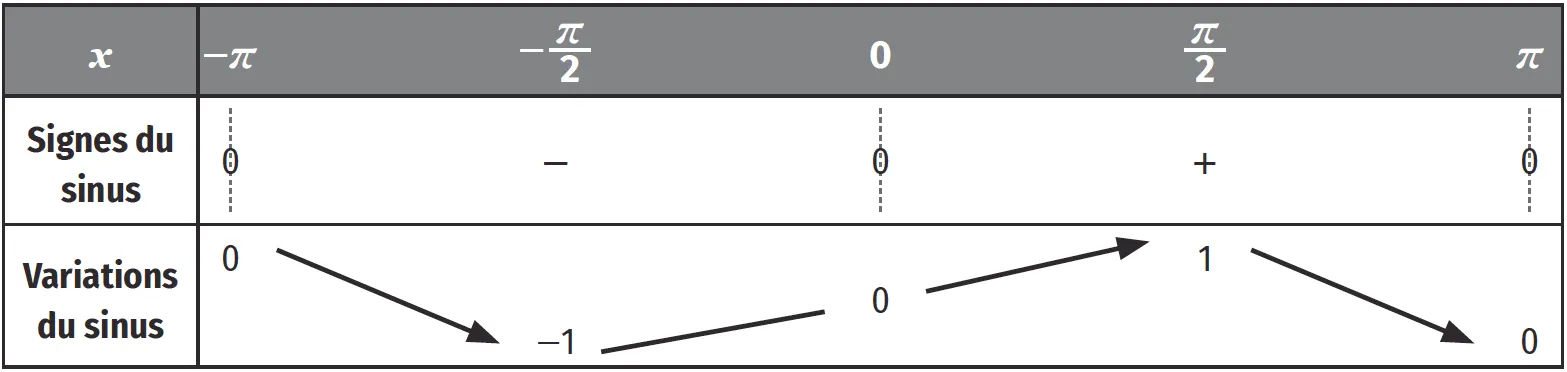
Les fonctions cosinus et sinus étant 2\pi-périodiques, on peut restreindre l'étude du signe et des variations sur l'intervalle [-\pi \:; \pi].
Fonction cosinus :
Le zoom est accessible dans la version Premium.
Fonction sinus :
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Les variations de \cos dépendent du signe de -\sin .
2. Les variations de \sin dépendent du signe de \cos .
2. Les variations de \sin dépendent du signe de \cos .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On considère la fonction g : x \mapsto \dfrac{1}{\cos (x)}.
1. Donner l'ensemble de définition de g .
2. Dresser le tableau de variations de g sur ]-\dfrac{\pi}{2} \:; \dfrac{\pi}{2}[.
1. Donner l'ensemble de définition de g .
2. Dresser le tableau de variations de g sur ]-\dfrac{\pi}{2} \:; \dfrac{\pi}{2}[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. \cos (x)=0 \Leftrightarrow x=\dfrac{\pi}{2}+k \pi avec k \in \mathbb{Z}. La fonction g est donc définie pour tous les réels sauf pour x=\dfrac{\pi}{2}+k \pi avec k \in \mathbb{Z}.
2. La fonction g est de la forme \dfrac{1}{v} où v est une fonction dérivable et non nulle sur ] \dfrac{-\pi}{2}\: ; \dfrac{\pi}{2}[.
v(x)=\cos (x) et v^{\prime}(x)=-\sin (x). On en déduit que, pour tout x \in ] \dfrac{-\pi}{2}\: ; \dfrac{\pi}{2}\left[, g^{\prime}(x)=\dfrac{-(-\sin (x))}{\cos ^{2}(x)}=\dfrac{\sin (x)}{\cos ^{2}(x)}\right. .
Le signe de g'(x) est alors le même que le signe de \sin(x) sur ] \dfrac{-\pi}{2}\: ; \dfrac{\pi}{2}[.
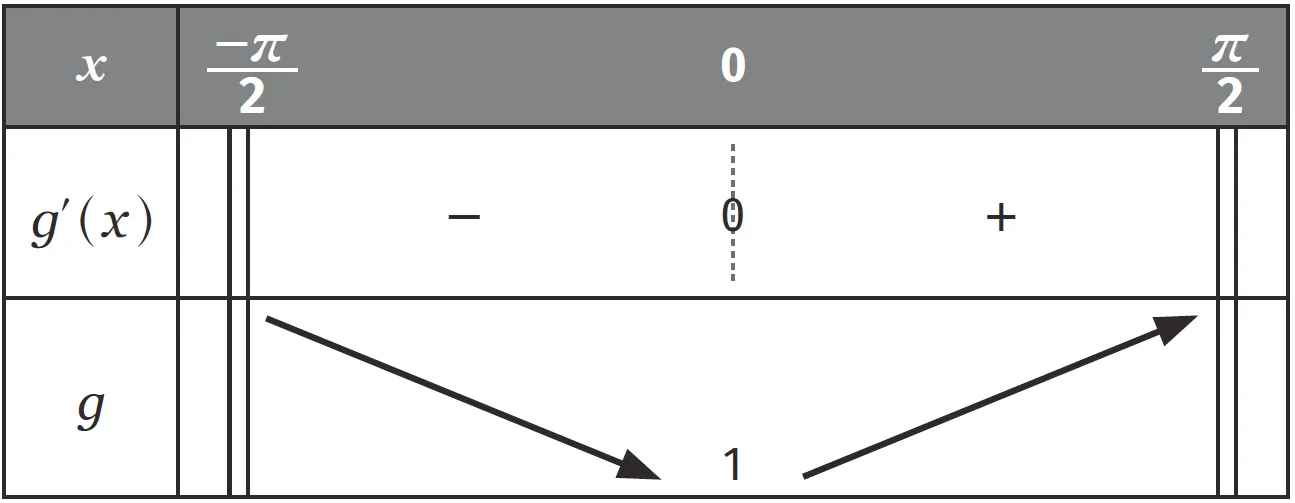
2. La fonction g est de la forme \dfrac{1}{v} où v est une fonction dérivable et non nulle sur ] \dfrac{-\pi}{2}\: ; \dfrac{\pi}{2}[.
v(x)=\cos (x) et v^{\prime}(x)=-\sin (x). On en déduit que, pour tout x \in ] \dfrac{-\pi}{2}\: ; \dfrac{\pi}{2}\left[, g^{\prime}(x)=\dfrac{-(-\sin (x))}{\cos ^{2}(x)}=\dfrac{\sin (x)}{\cos ^{2}(x)}\right. .
Le signe de g'(x) est alors le même que le signe de \sin(x) sur ] \dfrac{-\pi}{2}\: ; \dfrac{\pi}{2}[.
Le zoom est accessible dans la version Premium.
Pour s'entraîner
exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1.On identifie les fonctions de référence en jeu : ici, la fonction inverse et la fonction cosinus.
La fonction inverse étant définie pour tout réel non nul, il suffit d'écarter les zéros de la fonction cosinus ; c'est-à-dire les valeurs de x vérifiant \cos(x) = 0 .
Une fois les valeurs interdites déterminées, la fonction g est alors définie pour tous les réels excepté ces valeurs.
2.On calcule la dérivée et on détermine son signe en faisant attention aux valeurs interdites.
On déduit les variations de g à partir du signe de la dérivée.
2.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah