Concevoir un pendule comptant les secondes

Un pendule pesant est un système mécanique oscillant selon une certaine période. L'angle en degré que fait la ficelle avec la verticale est donné par la fonction $\alpha :t\mapsto 30\cos \left(\sqrt{\frac{g}{\ell }}\times t\right)$ où $g=9,81$ m·s^-2 est l'intensité de pesanteur terrestre et $\ell$ la longueur du fil en mètre.
Questions préliminaires :

1. Calculer et interpréter $\alpha (0).$

2. Le but étant de compter les secondes à l'aide du pendule, quelle période doit-on obtenir ?

Lancer GeoGebra en mode graphique.


1. Créer un curseur pour la longueur du fil $\ell$ compris entre $0$ et $1,5$ avec un pas de $0,01$ puis tracer la fonction $\alpha .$

2. Adapter l'échelle des axes.


3. En utilisant le menu intersection, proposer une manière précise de trouver la période.

4. Quel effet a la longueur $\ell$ sur la période ?

5. Répondre alors à l'objectif en déterminant la longueur $\ell$ cherchée au centimètre près.

Nous allons tracer la courbe représentative de $\alpha$ pour plusieurs valeurs de $\ell .$

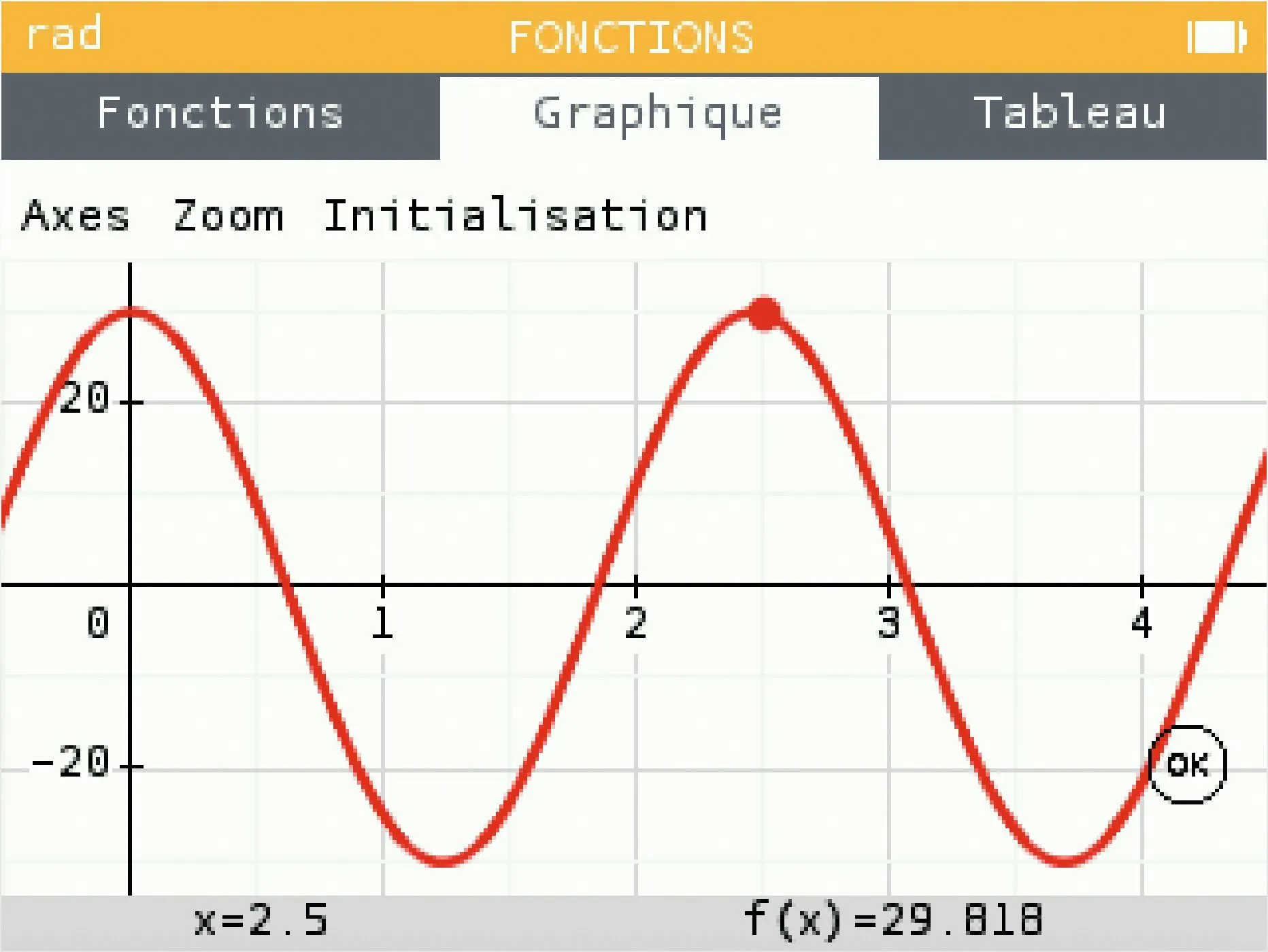
1. Tracer la courbe de $\alpha$ pour $\ell =1,5$ m. Régler la fenêtre correctement.

2. À l'aide d'une droite, trouver précisément la période de ce signal.

3. Comment évolue la période si on réduit la longueur du fil ?

4. En mettant en œuvre, à la main, un algorithme de dichotomie sur la longueur du fil et en reprenant les questions 1 et 2, trouver la longueur, arrondie au centimètre près, afin d'obtenir la période voulue.

1. Vérifier, par le calcul, que $\text{T}=\frac{2\pi }{\sqrt{g}}\sqrt{\ell }$ est bien une période des oscillations.

2. a. Lancer le tableur puis compléter la première colonne pour indiquer la longueur du fil en allant de 0 m à 1,5 m avec un pas de 0,1 m.

b. Utiliser la deuxième colonne pour indiquer la durée en seconde de la période correspondant à chaque valeur de $\ell .$

c. En déduire une valeur approchée de $\ell$ à 0,1 m près.

3. a. Changer les valeurs de $\ell$ pour avoir maintenant un pas de 0,01 m.

b En déduire alors une valeur de $\ell$ au centimètre près.