Livret algorithmique et programmation
Exercices
Exercices d'assimilation de Scratch (3/3)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Labyrinthe
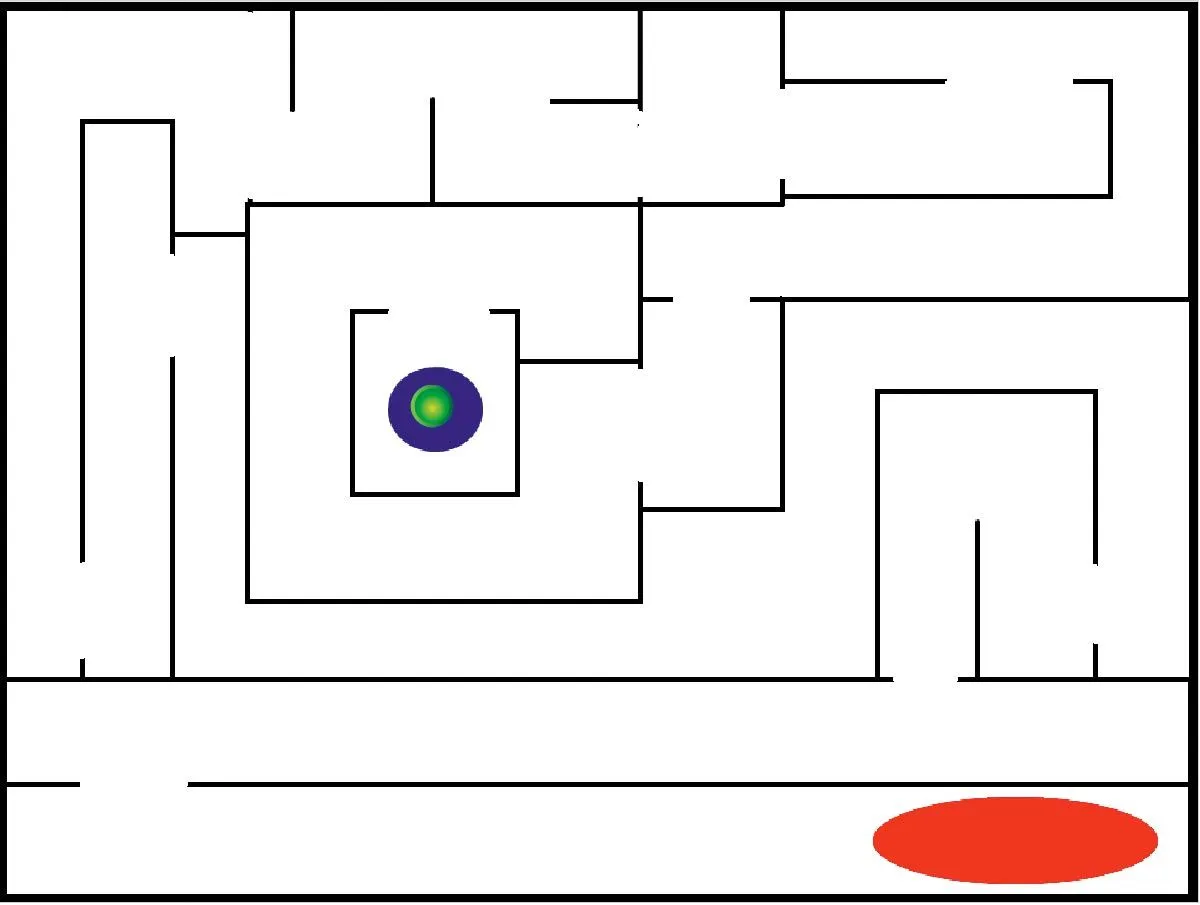
Le but est de créer un programme pour jouer au jeu du labyrinthe, avec un labyrinthe donné : le lutin vert part de la zone bleue pour aller dans la zone rouge.



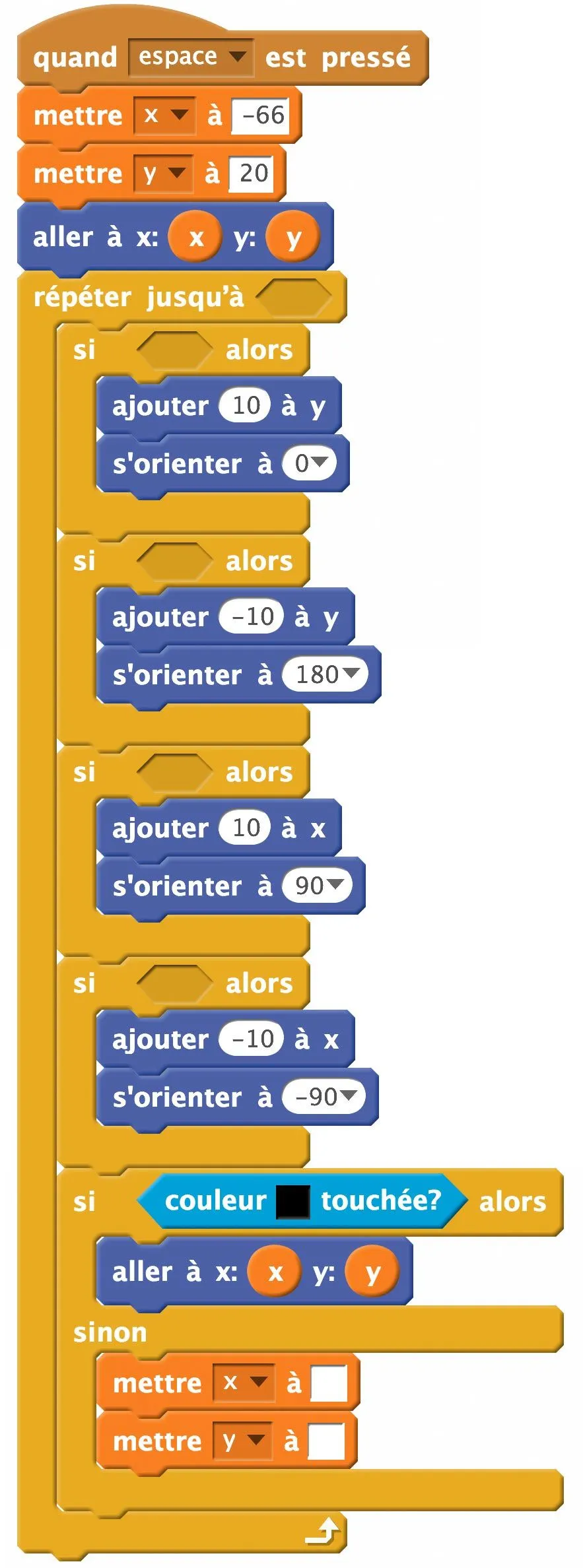
Voici le programme avec des trous :




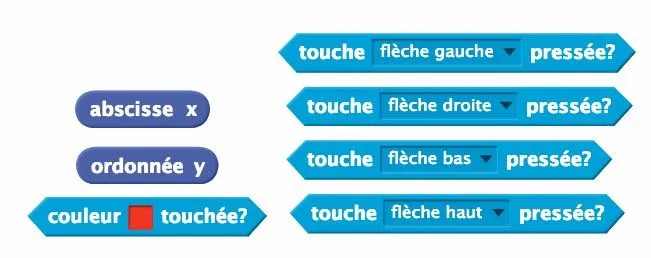
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18Approximation de solution
On veut trouver une approximation de la solution entre 0 et 1 de {-x^3 - 2x + 1 = 0}. On définit la fonction f (x) = -x^3 - 2x + 1. On sait que {f (0) > 0} et que {f (1) \lt 0}. Écrivez un programme qui permette de calculer lʼimage par f du point milieu, cʼest-à-dire f \left(\dfrac{1}{2}\right). Si f \left(\dfrac{1}{2}\right) \lt 0, alors on cherche cette fois la solution dans [0,\dfrac{1}{2}], par la même méthode, sinon dans [\dfrac{1}{2} \text{,} 1].
1. Faites un programme qui répète ce procédé cent fois pour calculer une approximation de la solution.
1. Faites un programme qui répète ce procédé cent fois pour calculer une approximation de la solution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19Carré de Sierpinski


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Suppléments numériques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Exercice numérique
On considère les deux figures suivantes, un triangle équilatéral et un rectangle, où x représente un nombre positif quelconque.

On a créé les programmes suivant sur qui, après avoir demandé la valeur de x à l'utilisateur, construisent les deux figures précédentes. Dans ces deux programmes, les lettres A, B, C et D remplacent des nombres. Donner des valeurs à A, B, C et D pour que ces deux programmes permettent de construire ces figures puis préciser quel programme permet de construire quelle figure.

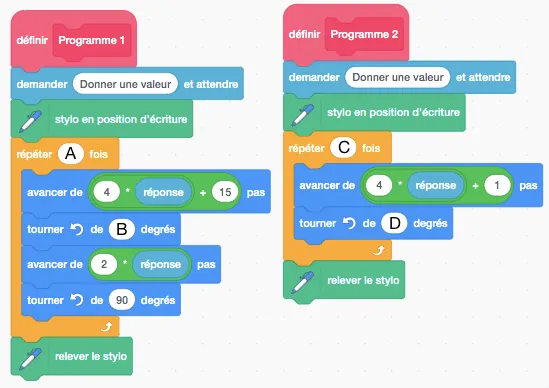

On a créé les programmes suivant sur qui, après avoir demandé la valeur de x à l'utilisateur, construisent les deux figures précédentes. Dans ces deux programmes, les lettres A, B, C et D remplacent des nombres. Donner des valeurs à A, B, C et D pour que ces deux programmes permettent de construire ces figures puis préciser quel programme permet de construire quelle figure.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Exercice numérique
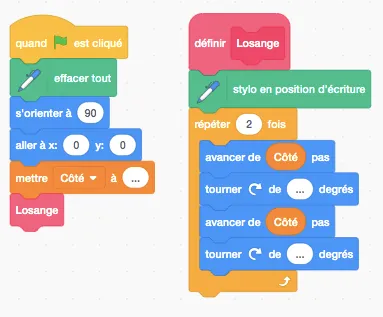
Compléter le programme suivant en remplaçant les pointillés par les bonnes valeurs afin que celui‑ci trace le losange suivant.





Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


