Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 2
Exercices
Manipuler des nombres entiers
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Échauffement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13
Écrire en toutes lettres les nombres suivants.
1. 41,2
2. 7,89
3. 125
4. 41,23
5. 74,589
6. 80,32
7. 745,7
8. 5 697,08
9. 0,0005
10. 5,0307
11. 74,98
12. 45,21
13. 9,637
14. 78,95
15. 4,38
16. 7,84
17. 0,047
18. 0,388
19. 4,23
20. 5,057
21. 4,207
1. 41,2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14Écrire les nombres suivants en écriture décimale
Identifier leurs parties entières et leurs parties décimales.
1. Cinquante-deux et trois cent quarante-trois millièmes.
2. Cent dix et quinze centièmes.
3. Mille trois cent quarante-cinq et douze centièmes.
4. Cinq et cent quatre-vingt-treize millièmes.
1. Cinquante-deux et trois cent quarante-trois millièmes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15
Réécrire les nombres sans zéros "inutiles".
1. 41,04
2. 3,750
3. 04,504
4. 600,00
5. 007
6. 1 001,01
1. 41,04
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
Compléter les égalités ci-dessous.
1. 45 \text{,} 33 = 45 + \dfrac{33}{...}
2. 17 \text{,} 298 = 17 + \dfrac{298}{...}
3. 5 \text{,} 4 = 5 + \dfrac{...}{10}
4. 417 \text{,} 5689 = 417 + \dfrac{...}{10 \: 000}
5. 51 \text{,} 36 = ... + \dfrac{36}{100}
6. 79 \text{,} 9 = ... + \dfrac{9}{10}
7. 2 \text{,} 22 = ... + \dfrac{...}{...}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
On considère le nombre 145,37.
1. Identifier le chiffre des dizaines et le chiffre des dixièmes de ce nombre.
2. Multiplier (sans opération) ce nombre par 10. Identifier le chiffre des dizaines du résultat. Quel est le chiffre des unités ?
1. Identifier le chiffre des dizaines et le chiffre des dixièmes de ce nombre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
Comparer les nombres suivants.
1. 45,8 et 37,9
2. 490,1 et 490,1000
3. 0,099 et 0,1
4. 123,01 et 122,99
5. 9 876,54 et 9 876,5399
6. 5,38 et 5,59
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
Décomposer les nombres comme dans l'exemple.
54 \text{,} 36 = 54 + \dfrac{36}{100} = 54 + \dfrac{3}{10} + \dfrac{6}{100}.
54 \text{,} 36 = 54 + \dfrac{36}{100} = 54 + \dfrac{3}{10} + \dfrac{6}{100}.
1. 3,912
2. 984,4
3. 24,1
4. 52,3679
5. 0,123
6. 41,01
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
Créer un tableau où l'on indiquera les chiffres des centaines, des dizaines, des unités, des dixièmes, des centièmes et des millièmes pour chaque nombre suivant.
| Nombre | Centaines | Dizaines | Unités | Dixièmes | Centièmes | Millièmes |
| 405,127 |
|
|
|
|
|
|
| 29,507 |
|
|
|
|
|
|
| 729,1 |
|
|
|
|
|
|
| 842,999 |
|
|
|
|
|
|
| 459,017 |
|
|
|
|
|
|
| 100,89 |
|
|
|
|
|
|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
Intercaler un nombre décimal entre chaque couple de nombres suivants.
1. 1 et 4,5
2. 0,59 et 0,69
3. 4,7 et 4,8
4. 5,59 et 5,6
5. 0,9999 et 1
6. 124 et 124,001
7. 85,12 et 85,1205
8. 3,33 et 3,333
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
Donner un encadrement des nombres suivants par deux entiers successifs.
1. 4,01
2. 0,5
3. 12,005
4. 0,9999
5. 1 946,7
6. 42,49
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Les listes de nombres suivantes sont-elles rangées par ordre croissant ?
1. 4,36 ; 9,7 ; 10 ; 16,78 ; 16,79
2. 0,264 ; 1,34 ; 1,399 ; 7,8 ; 100
3. 4,3 ; 4,1 ; 3,36 ; 2,77 ; 0
1. 4,36 ; 9,7 ; 10 ; 16,78 ; 16,79
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Les listes de nombres suivantes sont-elles rangées par ordre décroissant ?
1. 0,999 ; 0,87 ; 0,6 ; 0
2. 3,2 ; 4,789 ; 5 ; 6,6 ; 98,412
3. 4,56 ; 3,99 ; 5,013 ; 5,0103
1. 0,999 ; 0,87 ; 0,6 ; 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Grâce aux inégalités suivantes, donner une valeur approchée par excès puis par défaut des nombres suivants.
1. 4,7 \text{\textless} 4,71 \text{\textless} 4,8. Valeur approchée de 4,71 au dixième.
2. 17 \text{\textless} 17,99 \text{\textless} 18. Valeur approchée de 17,99 à l'unité.
3. 19,99 \text{\textless} 19,993 \text{\textless} 20. Valeur approchée de 19,993 au centième.
4. 190 \text{\textless} 197 \text{\textless} 200. Valeur approchée de 197 à la dizaine.
5. 431,567 \text{\textless} 431,5671 \text{\textless} 431,568. Valeur approchée de 431,5671 au millième.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Donner une valeur approchée (par excès et par défault) de 21,2 au dixième.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Entraînement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Donner, sans poser de calcul, le chiffre des centaines et le chiffre des centièmes des résultats des opérations suivantes.
| Opérations | Centaines | Centièmes |
| 1 257,89 \div 10 |
|
|
| 124,657 \times 10 |
|
|
| 594,367 \times 100 |
|
|
| 451 \div 100 |
|
|
| 127,985 \div 1 000 |
|
|
| 0,9874 \times 1 000 |
|
|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
Donner pour chaque nombre une écriture décimale puis l'écrire en toutes lettres.
1. 12 + \dfrac{7}{10} + \dfrac{1}{1 \: 000}
2. \dfrac{725}{1 \: 000}
3. \dfrac{423}{10}
4. \dfrac{5 \: 890}{10}
5. 43 + \dfrac{56}{100}
6. 6 + \dfrac{31}{1 \: 000}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
Compléter le tableau suivant avec les centaines et les centièmes.
| Vaut |
| Dizaines | Unités | Dixièmes |
|
|
|
|
|
|
|
|
| 1 dizaine |
|
|
|
|
|
| 1 unité |
|
|
|
|
|
| 1 dixième |
|
|
|
|
|
|
|
|
|
|
|
|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
Donner les résultats des opérations suivantes en écriture de fraction décimale sans poser de calcul.
1. 5 487,12 \times 10
2. 0,032 \times 1 000
3. 0,03 \times 100
4. 345 \times 10
5. 1,0354 \times 100
6. 108,9 \times 10
1. 5 487,12 \times 10
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31
Donner les résultats des opérations suivantes en écriture de fraction décimale sans poser de calcul.
1. 41,3 \div 10
2. 0,345 \div 10
3. 9 715,32 \div 100
4. 0,0304 \div 100
5. 124,9 \div 1 000
6. 0,1509 \div 1 000
1. 41,3 \div 10
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
Donner sans calcul le résultat des opérations suivantes et dire à quelle opération cela correspond.
1. (412,3 \times 10) \div 100
2. (59,32 \div 10) \times 1 000
3. (45,987 \div 100) \times 10
4. (0,384 \div 100) \times 1 000
5. (348,1 \times 10 000) \div 1 000
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
Les nombres entiers sont-ils des nombres décimaux ? Justifier votre réponse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
Parmi les nombres suivants, dire lesquels sont entiers.
35\text{,}00 ; \dfrac{590}{10} ; 45 + \dfrac{7 \: 900}{1 \: 000} ; 457\text{,}01 ; 36 + \dfrac{560}{100} ; 1 + \dfrac{3 \: 600}{100}
35\text{,}00 ; \dfrac{590}{10} ; 45 + \dfrac{7 \: 900}{1 \: 000} ; 457\text{,}01 ; 36 + \dfrac{560}{100} ; 1 + \dfrac{3 \: 600}{100}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
Donner les valeurs approchées des nombres suivants.
1. 435,7 : par défaut à la dizaine.>
2. 12,38 : par excès au dixième.
3. 497,308 : par défaut au centième.
4. 351,7 : par excès au millième.
5. 12,74 : par excès à la centaine.
6. 45,3984 : par défaut au millième.
1. 435,7 : par défaut à la dizaine.>
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
Lors du grand prix de Formule 1 d'Australie 2012, le pilote Jenson Button a remporté la course.
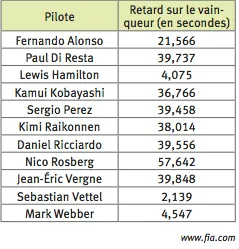On donne dans le tableau avec le retard des pilotes qui ont terminé la course avec moins d'un tour de retard. Quel est le podium de cette course ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37Vrai ou faux ?
Si c'est faux, corriger.
1. 42,6 est la valeur approchée par défaut au dixième de 42,61.
2. 59,82 est la valeur approchée par excès au dixième de 59,815.
3. 0,36 est la valeur approchée par défaut au centième de 0,3699.
4. 0 est la valeur approchée par défaut au centième de 0,00999.
5. 13,56 est la valeur approchée par excès au centième de 13,54996.
6. 11,3 est la valeur approchée par excès au dixième de 11,39.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
Compléter le tableau pour chaque nombre.
1. 1,7
2. 13
3. 0,56
4. 1,409
1. 1,7
| Précision | valeur approchée par défaut | valeur approchée par excès |
| 0,01 |
|
|
| 0,1 |
|
|
| 1 |
|
|
| 10 |
|
|
2. 13
| Précision | Valeur approchée par défaut | valeur approchée par excès |
| 0,01 |
|
|
| 0,1 |
|
|
| 1 |
|
|
| 10 |
|
|
3. 0,56
| Précision | Valeur approchée par défaut | Valeur approchée par excès |
| 0,01 |
|
|
| 0,1 |
|
|
| 1 |
|
|
| 10 |
|
|
4. 1,409
| Précision | Valeur approchée par défaut | Valeur approchée par excès |
| 0,01 |
|
|
| 0,1 |
|
|
| 1 |
|
|
| 10 |
|
|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
Donner un encadrement au centième des nombres suivants.
1. 12,316
2. 0,0463
3. 9,2
4. 48,411
5. 41,314
6. 527,004
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
Ranger par ordre croissant les listes de nombres suivantes.
1. 4,89; 0,364; 0,004; 7; 4,84.
2. 1,24; 12,4; 10,4; 16,57; 15,006.
3. 51,48; 50,001; 48,637; 68,91; 59,45; 50,95; 50,0009.
1. 4,89; 0,364; 0,004; 7; 4,84.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
Ranger par ordre décroissant les listes de nombres suivantes.
1. 10,59; 14,13; 13,509; 10,612; 12,4; 11.
2. 0,65; 0,984; 1; 0,06; 0,5; 1,1.
3. 4,55; 12,2; 9,99; 11,11; 3,6982.
1. 10,59; 14,13; 13,509; 10,612; 12,4; 11.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
Dire si chaque liste est croissante ou décroissante et insérer le nombre donné à la bonne place.
1. 1,12; 3,45; 3,68; 4; 4,684; 5,6. Insérer 3,97.
2. 51,378; 50,999; 50,1; 50; 49,9823; 49,3. Insérer 50,04.
3. 0,568; 0,6; 0,69; 0,698; 0,7; 0,702; 0,75. Insérer 0,61.
1. 1,12; 3,45; 3,68; 4; 4,684; 5,6. Insérer 3,97.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
Comparer les deux nombres suivants : 11,59 et 12,01.
Justifier votre réponse.
La réponse à l'exercice suivant est-elle correcte ? Si c'est le cas, expliquer pourquoi, sinon la corriger.
La réponse à l'exercice suivant est-elle correcte ? Si c'est le cas, expliquer pourquoi, sinon la corriger.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
Écrire tous les nombres décimaux à quatre chiffres
qui s'intercalent entre 12,1 et 12,2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
Trier la liste d'avions suivantes.
D'abord par longueur croissante puis par envergure décroissante.
| Avion | Longueur (m) | Envergure (m) |
| Ouragan | 10,74 | 13,16 |
| Mystère IV | 12,85 | 11,12 |
| Mirage III | 8,22 | 14,77 |
| Mirage F1 | 15 | 8,4 |
| Super-Étendard | 14,31 | 9,6 |
| Mirage 2000 | 9,13 | 14,6 |
| Rafale | 15,3 | 10,9 |
D'abord par longueur croissante puis par envergure décroissante.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46 Le juste prix
Lors d'un jeu télévisé, un candidat doit trouver le juste prix au centième près d'un ordinateur portable d'une célèbre marque.
Sa première proposition est de 4 120,09 €. L'animateur l'informe que tous les chiffres utilisés sont les bons mais qu'ils sont dans le désordre. En réorganisant l'ordre des chiffres, il parvient à trouver le juste prix. Le nombre est en fait entier et impair. Le chiffre des centaines vaut la moitié du chiffre des milliers alors que le chiffre des dizaines en vaut le double. Quel est le juste prix de cet ordinateur ?
Sa première proposition est de 4 120,09 €. L'animateur l'informe que tous les chiffres utilisés sont les bons mais qu'ils sont dans le désordre. En réorganisant l'ordre des chiffres, il parvient à trouver le juste prix. Le nombre est en fait entier et impair. Le chiffre des centaines vaut la moitié du chiffre des milliers alors que le chiffre des dizaines en vaut le double. Quel est le juste prix de cet ordinateur ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compétition
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47Utilisation de la règle graduée
1. Mesure-t-on avec une règle graduée des valeurs exactes ou des valeurs approchées ?
2. En prenant comme unité le mètre, les règles utilisées couramment permettent-elles de donner des valeurs approchées de distances au dixième ? Au centième? Au millième ?
3. La règle graduée permet-elle de prendre des valeurs approchées par excès ou par défaut ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
Le rapporteur permet-il de mesurer des valeurs d'angles excates ou approchées ?
Le cas échéant, à quelle précision (on prend comme unité de base le degré d'angle) ? Par excès ou par défaut ?
Le cas échéant, à quelle précision (on prend comme unité de base le degré d'angle) ? Par excès ou par défaut ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49Pour comparer 2 nombres, il suffit de voir si leur différence est positive ou négative
1. Est-ce vrai ? En déduire une manière de comparer deux nombres grâce à la calculatrice.
2. Utiliser la calculatrice pour ranger par ordre croissant la liste de nombres suivante. 14,3; 11,789; 52; 0,671; 1,68412; 1475,15; 10,1010.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
Écrire tous les nombres décimaux à quatre chiffres qui s'intercalent entre 1,1 et 1,15 tels que le chiffre des millième est divisible par le chiffre des centièmes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51Donner tous les nombres qui vérifient simultanément les propositions suivantes
Le chiffre des unités est 2. Le chiffre des centièmes est le double de celui des unités. Le chiffre des dixièmes est le résultat de la multiplication par 2 du chiffre des centièmes. Le chiffre des centaines est égal à la moitié de 6. La somme du chiffre des unités et des centaines est égal au chiffre des dizaines.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
Ranger les nombres suivants dans l'ordre croissant, sans les réécrire différemment.
42 millièmes; 420 centièmes; 0,42; 0,0042 centaine.
42 millièmes; 420 centièmes; 0,42; 0,0042 centaine.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Socle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCM
1. Dans 8 175,29 le chiffre 2 est le chiffre des :
2. ... et 7 est le chiffre des :
3. Une écriture décimale de \dfrac{1 \: 428}{1 \: 000} est :
4. Une fraction décimale de 429,37 est :
5. A = 157 \text{,} 951 \times 100
6. B = 439 \text{,} 142 \div 1 \: 000
2. ... et 7 est le chiffre des :
3. Une écriture décimale de \dfrac{1 \: 428}{1 \: 000} est :
4. Une fraction décimale de 429,37 est :
5. A = 157 \text{,} 951 \times 100
6. B = 439 \text{,} 142 \div 1 \: 000
7. Avec a = 7,89 et b = 8,0012 :
8. Avec a = 4,013 et b = 4,009 :
9. 17,3 est encadré par :
10. Entre 11,899 et 11,9 on peut intercaler :
11. Ici le point d'abscisse 1,4 est :
12. Ici le point C représente le nombre :
8. Avec a = 4,013 et b = 4,009 :
9. 17,3 est encadré par :
10. Entre 11,899 et 11,9 on peut intercaler :
11. Ici le point d'abscisse 1,4 est :
12. Ici le point C représente le nombre :
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah