Mathématiques 6e
Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Mes Pages
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 2
Pas à pas
2. Comparer des nombres décimaux
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
Voici les tailles des membres de la famille d'Arthur, exprimées en mètres.

 a. Découper une bande de papier millimétré et placer les membres de la famille selon leur taille sur un axe.
a. Découper une bande de papier millimétré et placer les membres de la famille selon leur taille sur un axe.
b. Pour une photographie, la famille se range du plus petit au plus grand. Dans quel ordre seront-ils positionnés‑?
c. La meilleure amie d'Arthur fait 1,39 m. Est-elle plus grande que lui ?


b. Pour une photographie, la famille se range du plus petit au plus grand. Dans quel ordre seront-ils positionnés‑?
c. La meilleure amie d'Arthur fait 1,39 m. Est-elle plus grande que lui ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
- Comparer deux nombres, c'est dire si l'un est (strictement) plus petit que l'autre ou s'ils sont égaux.
- Avec a et b deux nombres, on a les notations suivantes.

- Ranger une liste de nombres par ordre croissant, c'est ranger ses nombres du plus petit au plus grand. La ranger par ordre décroissant, c'est ranger ses nombres du plus grand au plus petit.
- 1 ; 4,57 ; 7,8 ; 9,001 est une liste rangée par ordre croissant.
- 9,001 ; 7,8 ; 4,57 ; 1 est une liste rangée par ordre décroissant.
- Une fois qu'une liste de nombres est rangée par ordre croissant, il suffit de la prendre à l'envers pour la ranger par ordre décroissant.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
- Encadrer un nombre, c'est trouver un autre nombre strictement plus grand et un autre nombre strictement plus petit.
- 7 est encadré par 6,9 et 7,1 : 6,9 < 7 < 7,1.
- Intercaler un nombre entre deux autres nombres a et b, c'est trouver un nombre x qui est compris entre a et b : a < x < b.
- On peut intercaler 2,54 entre 2,5 et 2,6 : 2,5 < 2,54 < 2,6. Pour faire cela facilement, on se rappelle que 2,5 = 2,50 et 2,6 = 2,60. On a alors bien 2,50 < 2,54 < 2,60.
- Pour intercaler un nombre dans une liste triée, il faut le placer entre le nombre qui est juste « au-dessus » et celui qui est juste « en dessous ».
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Comparer deux nombres décimaux.
Comparer les nombres suivants : 0,99 et 2,01 puis 21,3 et 21,19.
- Pour comparer des nombres en écriture décimale, on suit la méthode suivante :
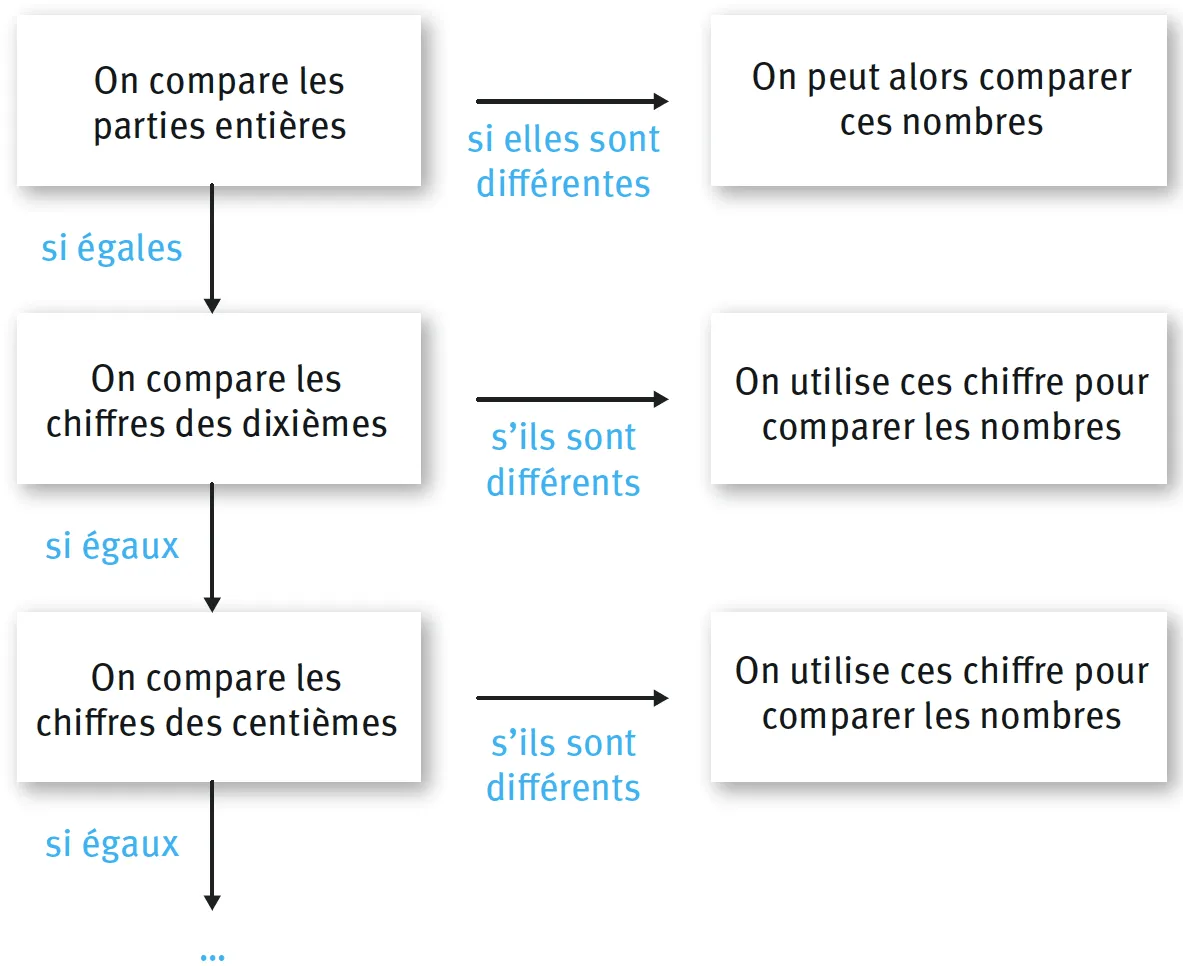
- Ici, avec 0,99 et 2,01 :
- La partie entière de 0,99 est 0. Celle de 2,01 est 2.
- 0 < 2 : les parties entières sont différentes, donc 0,99 < 2,01.
- Avec 21,3 et 21,19 :
- La partie entière de 21,3 et 21. Celle de 21,19 est 21.
- 21 = 21 : les parties entières sont égales, on compare donc les chiffres des dixièmes.
- 3 > 1, donc 21,3 > 21,19.
- Astuce : petit < GROS, GROS > petit.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5Comparer les couples de nombres décimaux suivants.
1. 2,78 et 2,82
2. 1,751 et 1,3
3. 4,59741 et 510
4. 187 451,1 et 0,2
5. 1,40000 et 1,4
6. 5,15 et 5,98
7. 7,54 et 6,91
8. 7,963 et 8
9. 42,42 et 42,142
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Ranger une liste de nombres décimaux.
Ranger la liste de nombres suivants par ordre décroissant : 0,43 ; 5,2 ; 7,99 ; 2,5 ; 9 ; 52 ; 13,127 ; 8. Placer 8,3 dans cette liste.
- On compare les différents nombres pour établir qui est le plus grand, et ainsi de suite. On obtient 52 > 13,127 > 9 > 8 > 7,99 > 5,2 > 2,5 > 0,43. On peut aussi, lorsque les nombres le permettent, les placer sur un axe puis « lire » l'axe dans le sens désiré.
- En lisant la liste, on voit que tous les nombres supérieurs à 8,3 sont 9 ; 13,127 et 52. Le plus petit est 9.
- Les nombres de la liste inférieurs à 8,3 sont 0,43 ; 2,5 ; 5,2 ; 7,99 ; 8. Le plus grand est 8. On intercale 8,3 entre 8 et 9 et on obtient la liste triée :
- 52 > 13,127 > 9 > 8,3 > 8 > 7,99 > 5,2 > 2,5 > 0,43.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6Placer les nombres suivants sur une droite graduée. En déduire un rangement en ordre croissant.
1. 5,1 ; 4,3 ; 7,8 ; 0,1 ; 7,8 ; 3,6.
2. 7,8 ; 3,5 ; 8,8 ; 0,5 ; 0,6.
3. 8,89 ; 8,78 ; 8,59 ; 9,32 ; 9,21.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7Trier par ordre croissant les listes de nombres suivants. Y placer le nombre 12,357.
1. 2,45 ; 10 154 ; 0,354 ; 5,10.
2. 12,0 ; 5,4 ; 2 ; 87,4511 ; 87,4523.
3. 0 ; 12,457 ; 78 ; 42,42 ; 89,1 ; 41,144 ; 1,45721455.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Intercaler un nombre décimal entre deux nombres décimaux.
Intercaler un nombre entre 5,57 et 5,58.
- Par exemple 5,57 <5,575 < 5,58. Pour se faciliter la tâche, on se rappelle que 5,57 = 5,570 !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 8Intercaler un nombre entre les couples de nombres suivants.
1. 7,1 et 7,2
2. 8 et 9
3. 0,014 et 0,016
4. 1,69 et 1,7
5. 5,4587 et 5,4588
6. 597,841 et 598,841
7 52,3 et 53,2
8. 999,99 et 1 000
9. 21,3 et 51,2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 9Intercaler deux nombres entre les couples de nombres suivants.
1. 4,8 et 4,9
2. 5 et 5,5
3. 0,02 et 0,2
4. 98 et 100
5. 54 et 54,05
6. 49 et 50,2
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille



