Mathématiques 6e

Enseignant en primaire ?

Accompagnez-nous dans le développement d'une nouvelle collection !

Mes Pages

Du primaire au collège

Ch. 1

Manipuler les nombres entiers

Ch. 2

Les nombres décimaux

Ch. 3

Addition, soustraction

Ch. 4

Multiplication, division décimale

Ch. 5

Fractions

Ch. 6

Proportionnalité

Ch. 7

Construction de droites

Construction de droites

Ouverturep. 115

Coursp. 116-119

2. Parallélisme, perpendicularité

Coursp. 120-122

3. Tracer une perpendiculaire

4. Tracer une parallèle

Construction de droites

Exercicesp. 126-127

Fiches de révision - Exclusivité numérique

Fiches de révision - Exclusivité numérique

Exercices de révision - Exclusivité numérique

Exercices de révision - Exclusivité numérique

Ch. 8

Distances et cercles

Ch. 9

Angles

Ch. 10

Symétrie axiale

Ch. 11

Triangles, rectangles et losanges

Ch. 12

Aire et périmètre

Ch. 13

Volumes

Nos dossiers d'actualité

Dossier d'actualité

Chapitre 7

Pas à pas

2. Parallélisme, perpendicularité

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Retenir

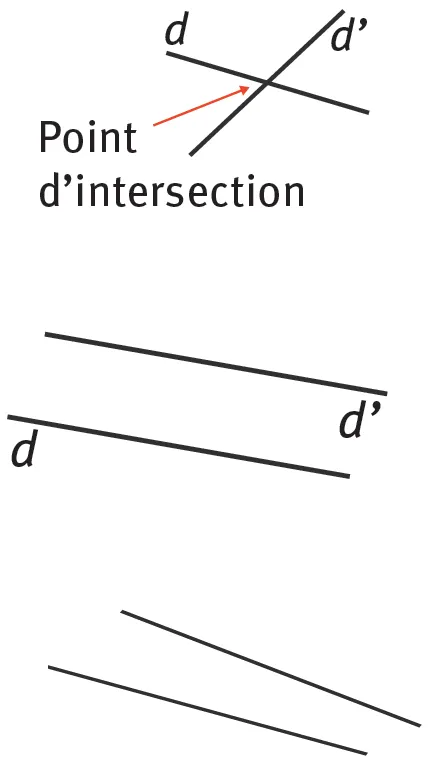
Lorsque deux droites distinctes se coupent, on dit qu'elles sont sécantes. L'endroit où elles se coupent est leur point d'intersection.
Si deux droites ne sont pas sécantes ou sont confondues on dit qu'elles sont parallèles.
- Notation : d // d'

Attention ! Ces deux droites n'ont pas l'air d'être parallèles, mais on ne les voit pas se couper !

Schéma : intersection de droites sécantes, parallèles et non parallèles.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Retenir

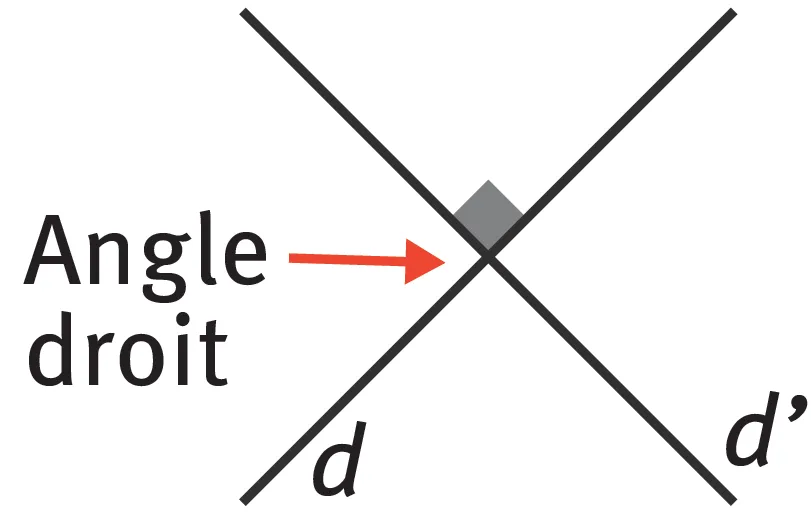
Quand deux droites se coupent en formant 4 angles superposables, on appelle ces angles des angles droits.

Icône graphique : croix noire épaisse, symbole fermeture/annulation.

Remarque :
Quand deux droites forment un angle droit, les trois autres angles sont forcément droits aussi.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Retenir

Deux droites qui se coupent en formant un angle droit sont dites perpendiculaires.

Notation : d \perp d'

Illustration : deux droites perpendiculaires formant un angle droit de 90 degrés.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 7
Pas parallèles

Que peut-on dire de deux droites qui ne sont pas parallèles?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 8
Point commun

Que peut-on dire de deux droites qui ont plus d'un point commun?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 9
Pas sécantes

Deux droites qui ne sont pas sécantes peuvent-elles être perpendiculaires ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Retenir

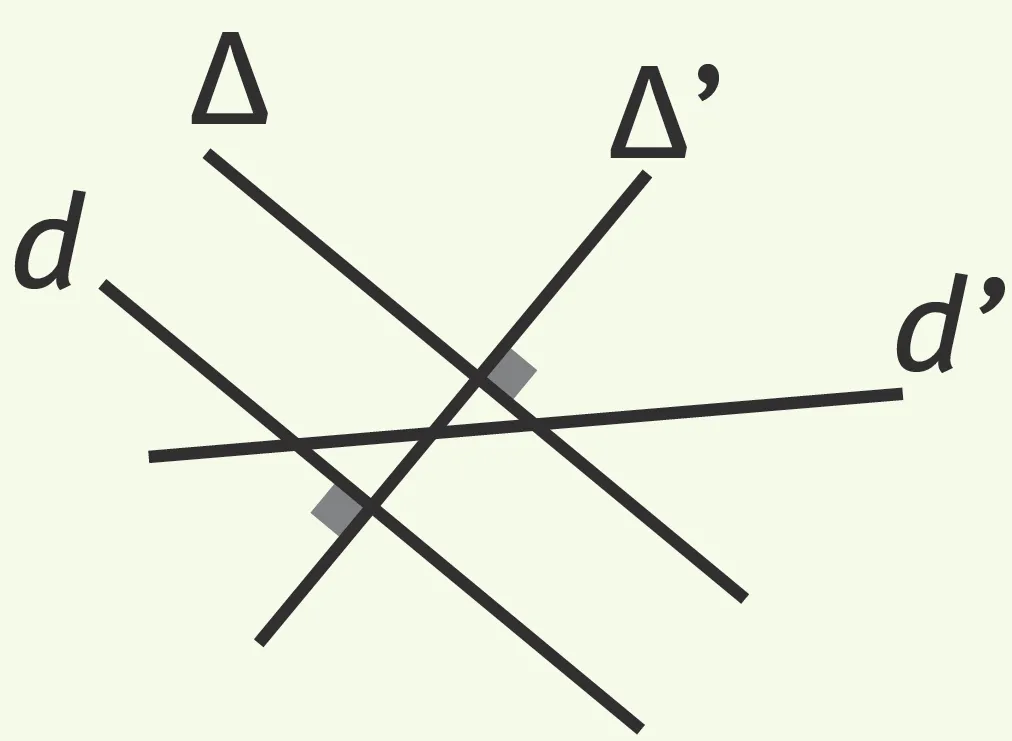
Étant donné un point et une droite, il existe une et une seule droite perpendiculaire à la droite passant par le point donné.
Propriété : Si deux droites sont perpendiculaires à une même droite, alors ces deux droites sont parallèles entre elles.
On le résume de la manière suivante: si d ⊥ Δ et si d' ⊥ Δ alors d // d'.

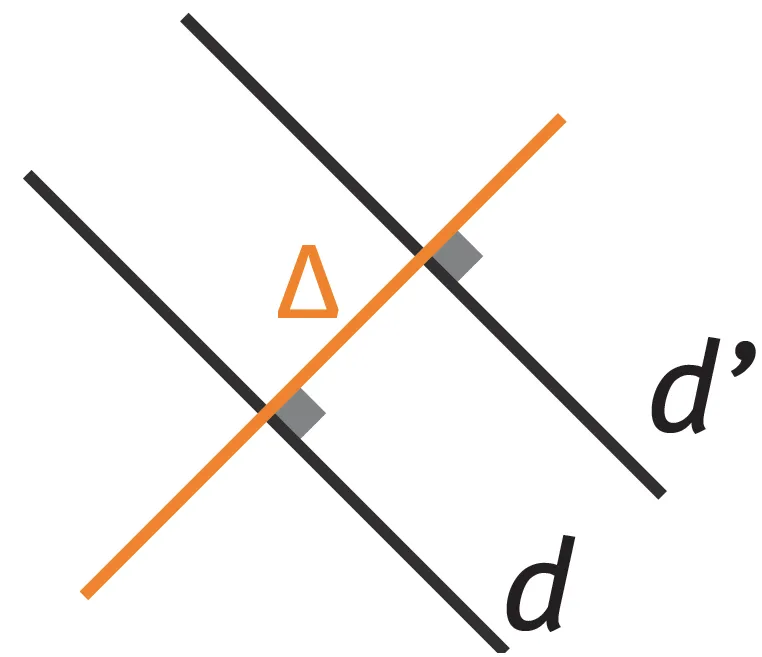
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Refaire
Utiliser cette propriété pour montrer que des droites sont parallèles

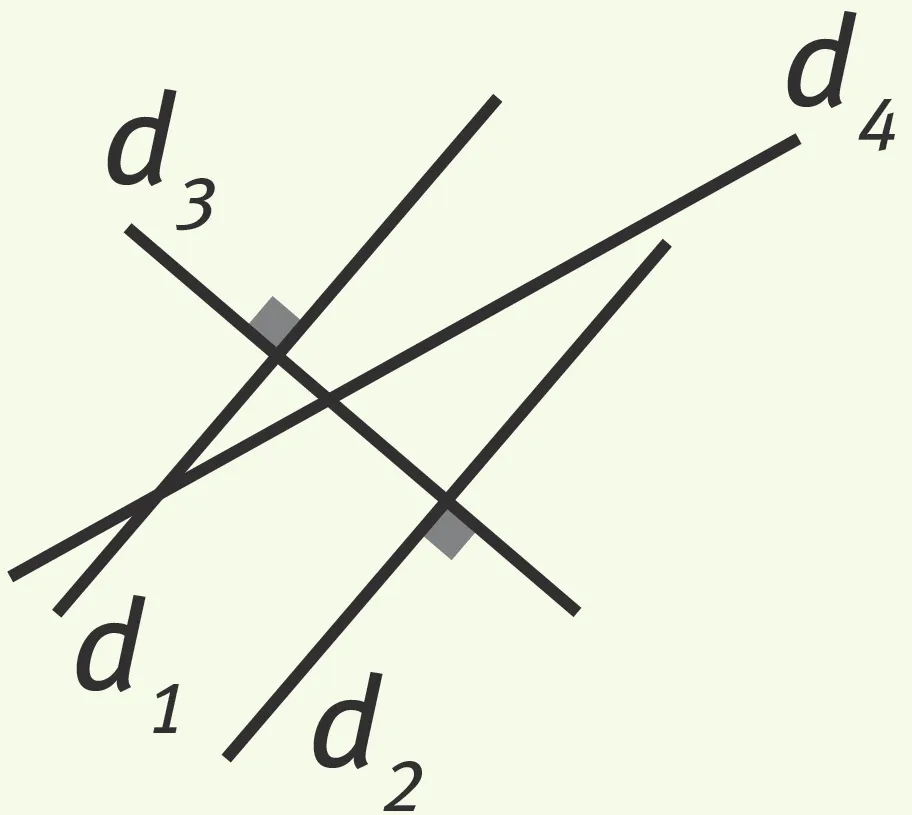
Dans la situation suivante, justifier que d_1et d_4 sont parallèles.

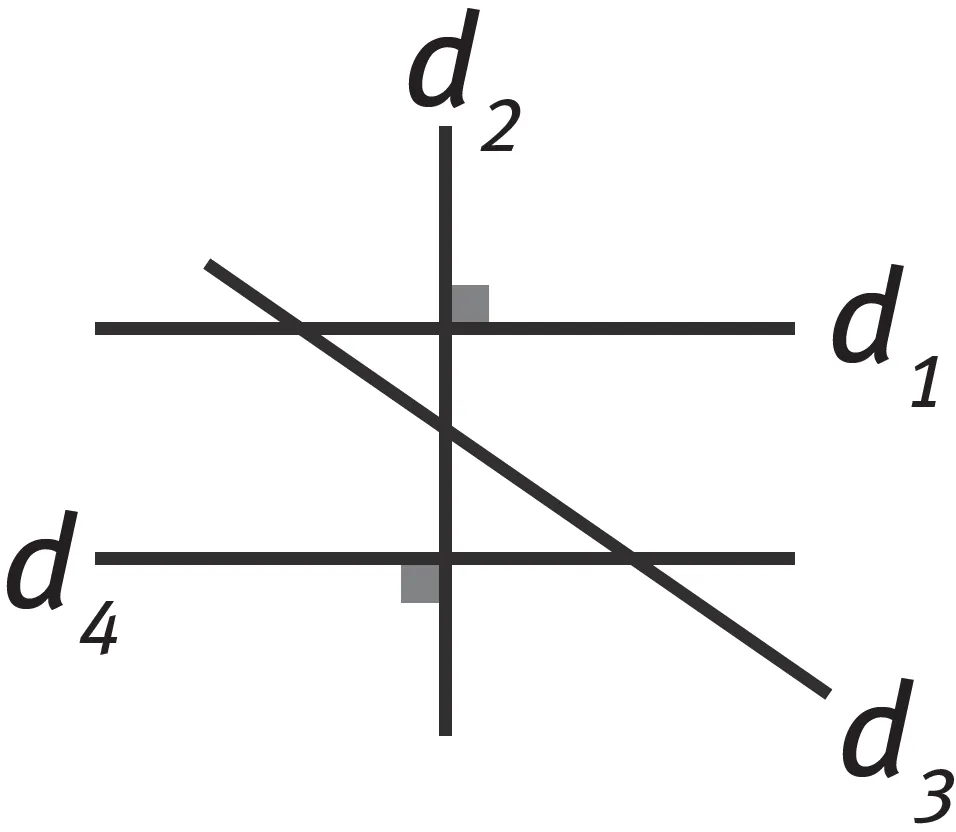
d_1 est perpendiculaire à d_2 : d_1 \perp d_2.
d_4 est perpendiculaire à d_2 : d_4 \perp d_2.
On sait que si deux droites sont perpendiculaires à une même droite alors elles sont parallèles.
Donc d_1 et d_4 sont parallèles.

Schéma géométrique : quatre droites, dont deux parallèles coupées par une sécante et une perpendiculaire.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 10
Parallèles

Schéma géométrique : deux droites coupées par deux sécantes, formant des angles. Illustration d'un exercice de géométrie.

Montrer que les droites d et \Delta sont parallèles.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 11
Parallèles

Schéma géométrique: quatre droites (d1, d2, d3, d4) se croisent, formant des angles. Deux intersections sont mises en évidence.

Montrer que les droites d_1 et d_2 sont parallèles.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Retenir

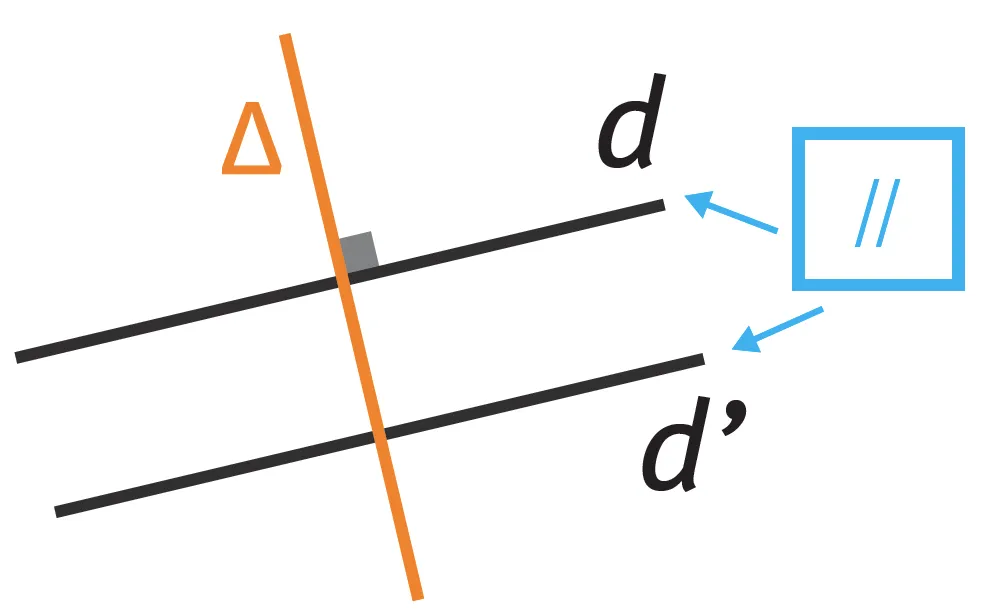
Propriété : Lorsque deux droites sont parallèles et qu'une troisième droite est perpendiculaire à l'une de ces deux droites, alors cette troisième droite est aussi perpendiculaire à l'autre droite.
On le résume de la manière suivante : si d // d' et si Δ ⊥ d alors Δ ⊥ d'.

Schéma : deux droites parallèles coupées par une sécante. Angles et parallélisme illustrés.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Refaire
Utiliser cette propriété pour montrer que ces deux droites sont perpendiculaires

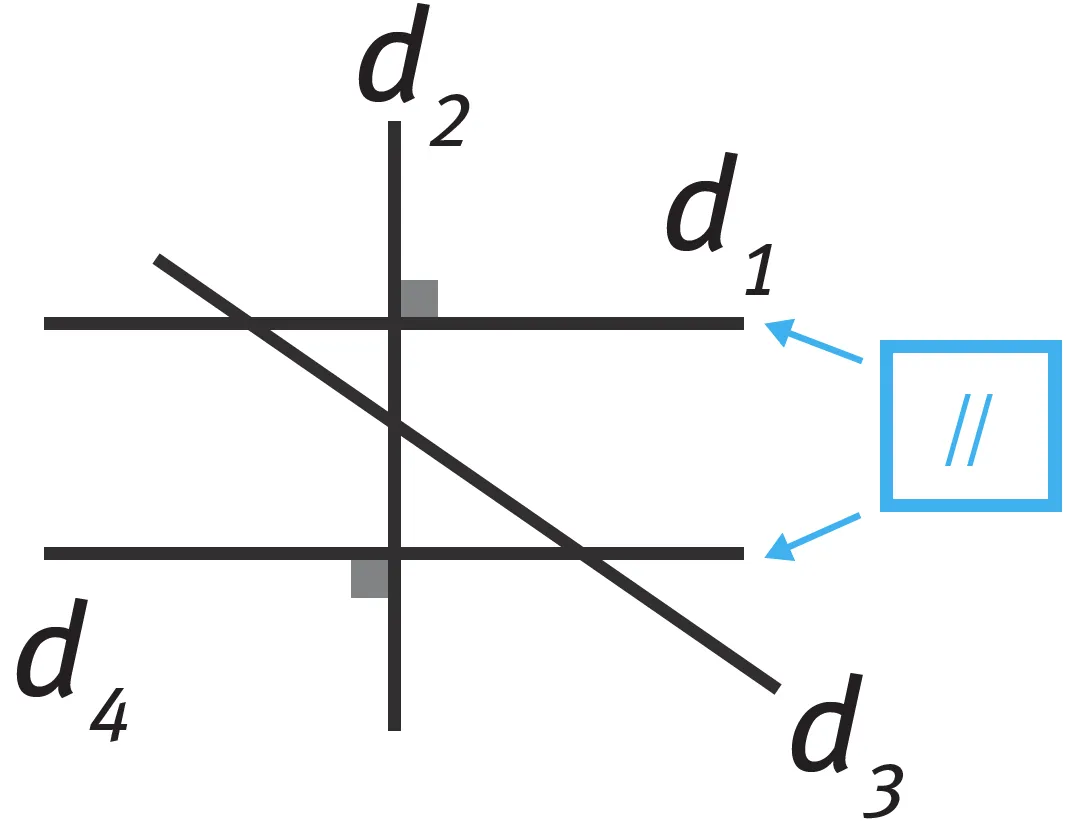
On sait que d_1 et d_4 sont parallèles. Justifier que d_2 et d_4 sont perpendiculaires.

d_1 est parallèle à d_4 : d_1 // d_4.
d_2 est perpendiculaire à d_1 : d_2 \perp d_1.
On sait que si deux droites sont parallèles, alors toute droite perpendiculaire à l'une est aussi perpendiculaire à l'autre.
Donc d_2 et d_4 sont perpendiculaires.

Schéma géométrique : deux droites parallèles coupées par une sécante. Angles correspondants et alternes-internes indiqués.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

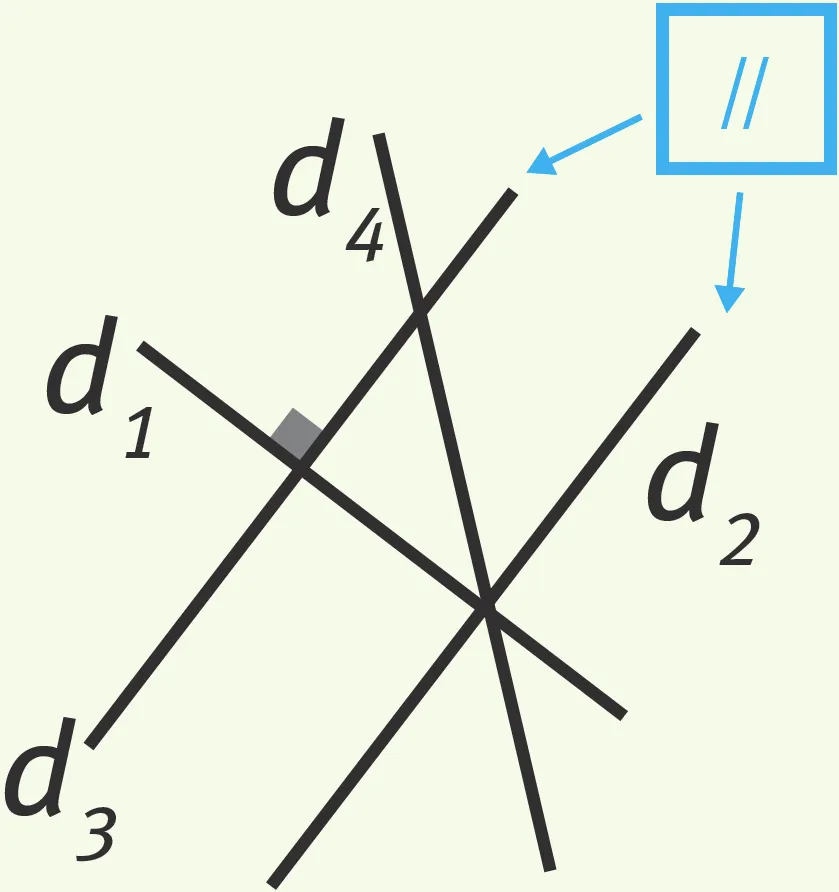
Exercice 12
Perpendiculaires

Schéma géométrique: quatre droites (d1, d2, d3, d4) se croisent; d2 et d4 sont parallèles.

1. Montrer que les droites d_1 et d_2 sont perpendiculaires.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

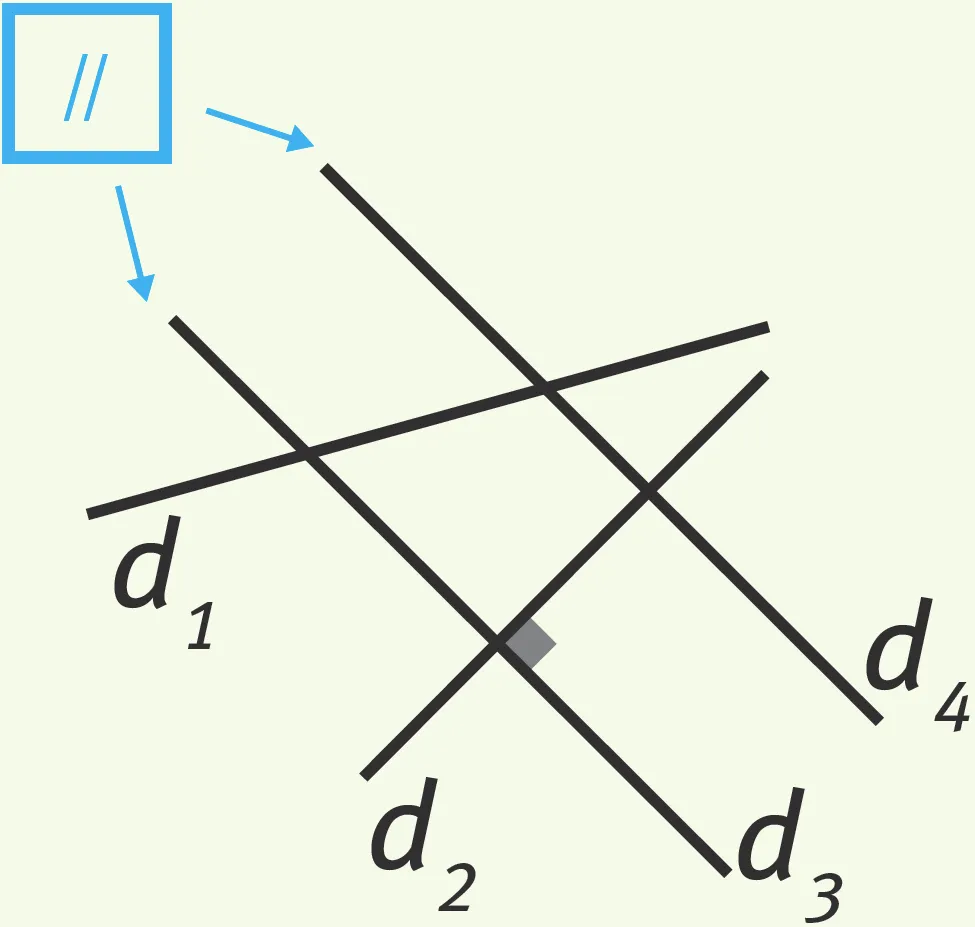
Exercice 13
Perpendiculaires

Schéma géométrique: quatre droites (d1, d2, d3, d4) se croisent, illustrant un parallélisme.

1. Montrer que les droites d_2 et d_4 sont perpendiculaires.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Retenir

En combinant les propriétés précédentes, on peut obtenir la propriété suivante.

Propriété : Si deux droites sont parallèles à la même droite alors ces deux droites sont aussi parallèles entre elles.
- On le résume en : si d // d' et d' // d'' alors d // d''.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

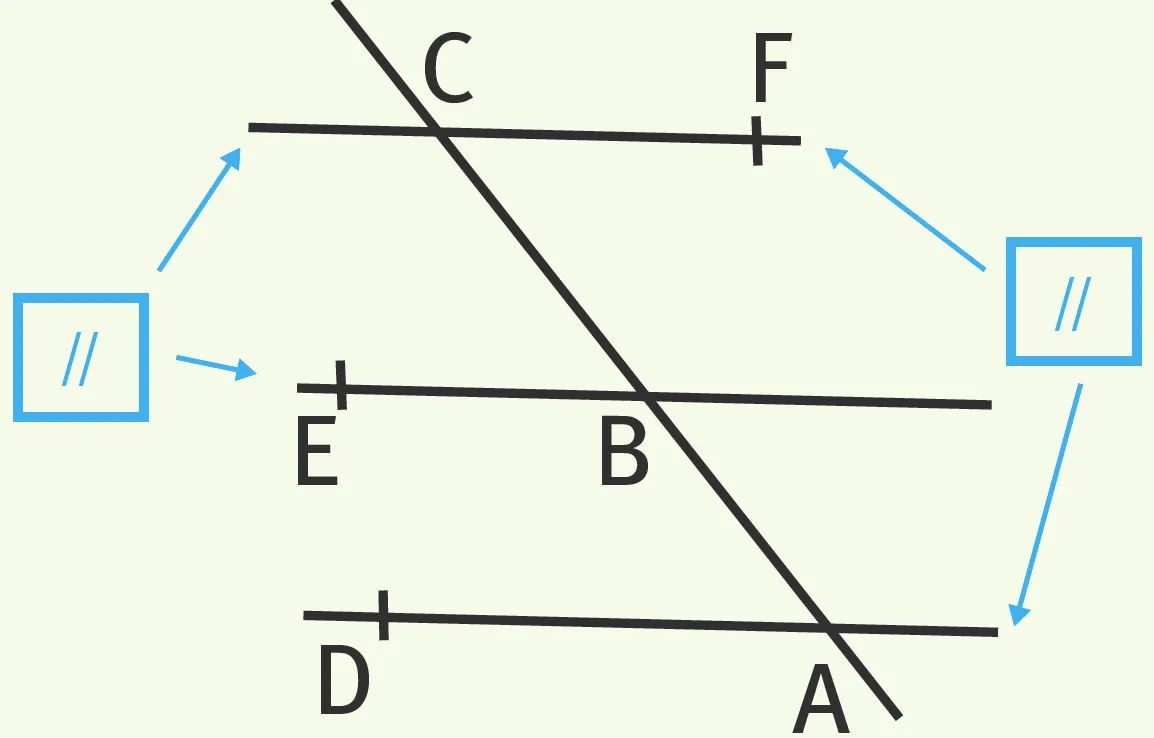
Refaire
Montrer que les droites d_1 et d_3 sont parallèles

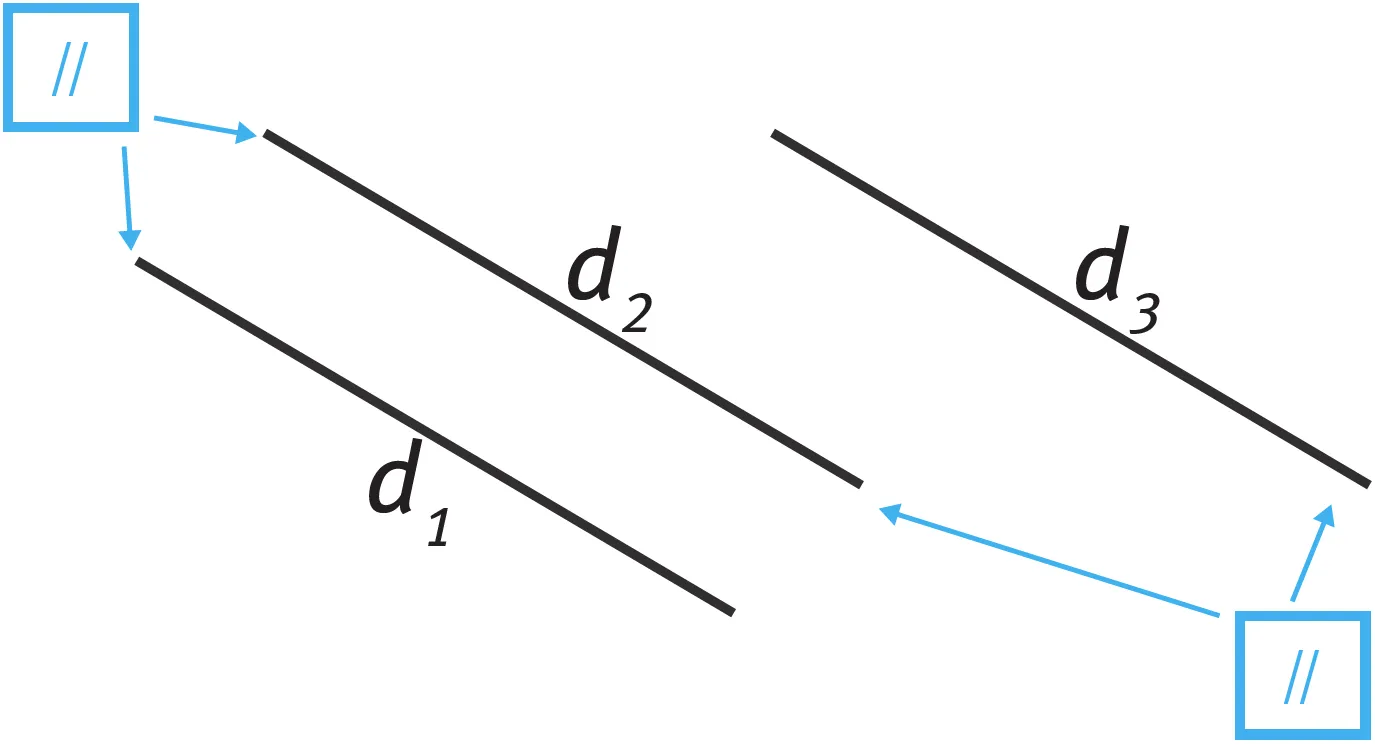
Schéma géométrique: démonstration du parallélisme de deux droites par angles correspondants.

On sait que d_1 // d_2 et que d_2 // d_3.

En utilisant la propriété précédente, on sait que d_1 et d_3 sont parallèles.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

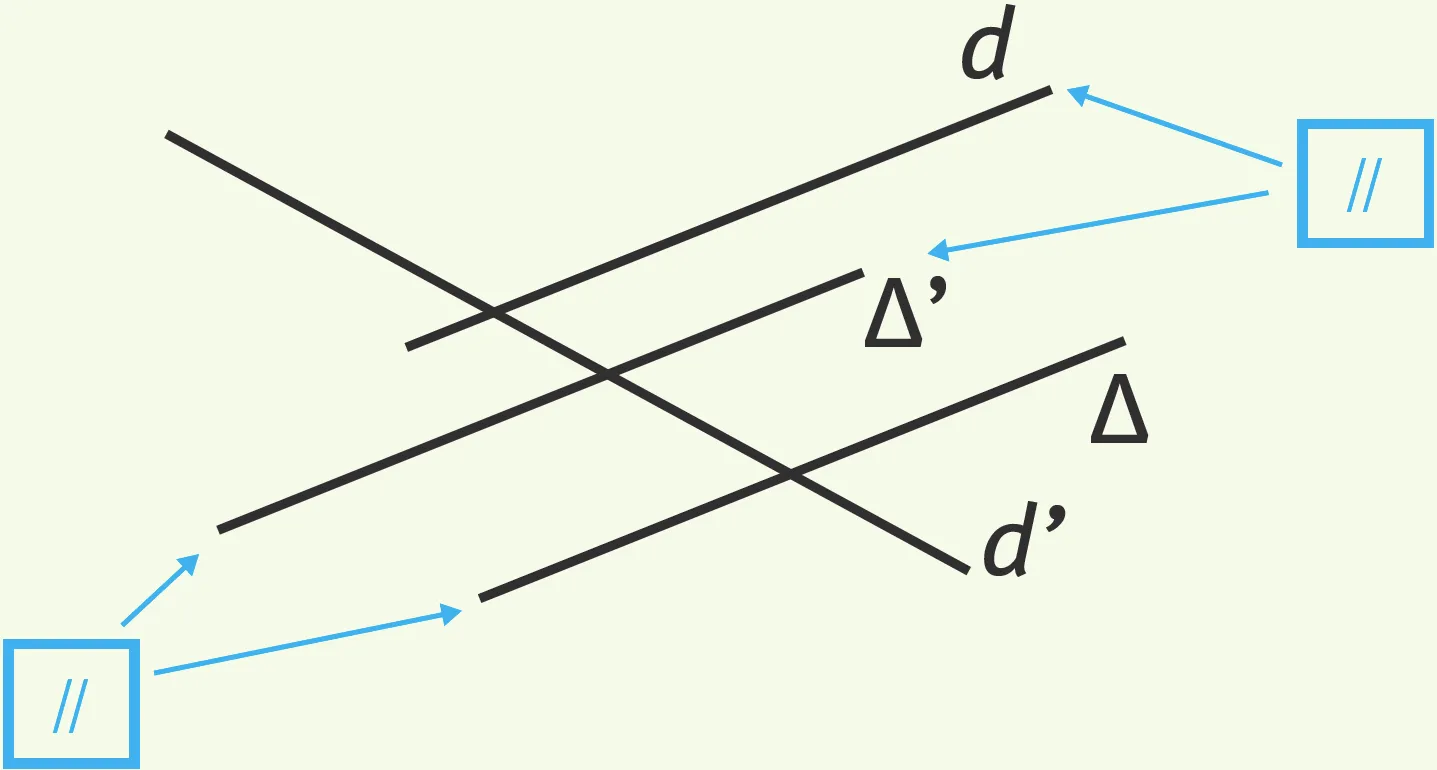
Exercice 14
Parallèles

Schéma : deux droites parallèles coupées par deux sécantes. Flèches bleues indiquant les angles correspondants.

1. Montrer que les droites d et \Delta sont parallèles.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 15
Parallèles

Schéma géométrique : droites parallèles coupées par une sécante. Angles correspondants et alternes-internes sont indiqués.

1. Montrer que les droites (AD) et (EB) sont parallèles.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.