Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 5
L'essentiel
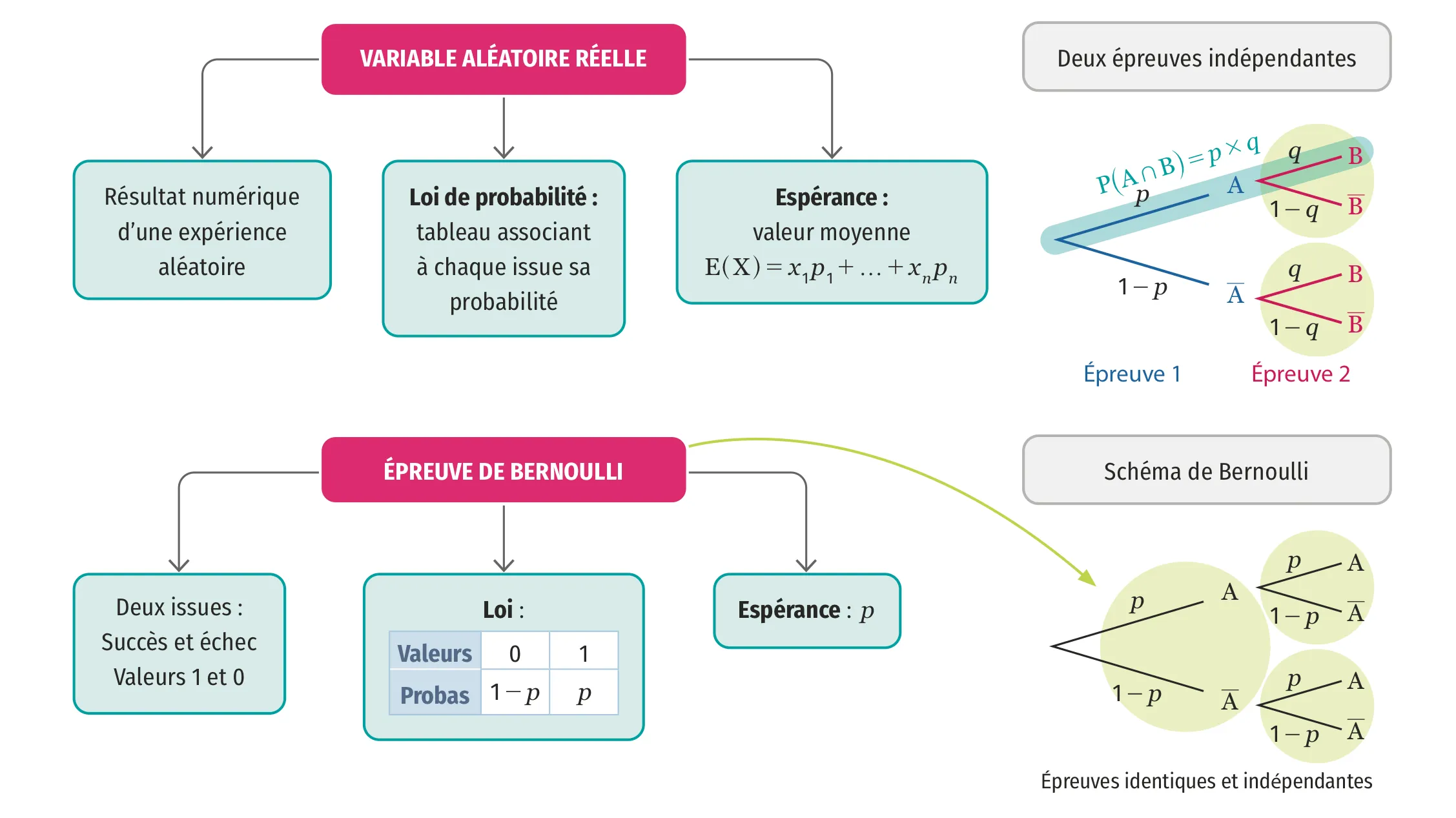
Variables aléatoires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fiche méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Donner la loi de probabilité d'une variable aléatoire \bf{X}
- Lister les valeurs prises par \text{X} et déterminer leurs probabilités. Vérifier que la somme des probabilités vaut 1.
- On synthétise ces résultats dans un tableau.
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Calculer l'espérance d'une variable aléatoire discrète
- Lorsque la loi de probabilité est donnée sous forme de tableau, on calcule l'espérance comme une moyenne pondérée : \mathrm{E}(\mathrm{X})=x_{1} p_{1}+x_{2} p_{2}+\ldots+x_{n} p_{n}.
- Sinon, commencer par construire la table de loi de probabilité de la variable aléatoire (voir point 1).
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Reconnaître une épreuve de Bernoulli
- L'expérience aléatoire ne doit avoir que deux issues (succès/échec ou 1/0)
- Le paramètre de l'épreuve de Bernoulli est la probabilité p du succès (ou d'obtenir 1).
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Utiliser un arbre de probabilité dans le cadre d'une expérience aléatoire à deux épreuves indépendantes
- La 1re série de branches décrit la 1re expérience, la 2e série de branches décrit la 2e, etc.
- Les événements sont indiqués au bout des branches, les probabilités correspondantes sont sur les branches.
- La probabilité d'un chemin (suite de branches) est le produit des probabilités situées sur les branches qui le composent. Les probabilités des chemins s'ajoutent entre elles.
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Reconnaître un schéma de Bernoulli
- On répète plusieurs fois, de manière identique et indépendante, une même expérience de Bernoulli.
- Les paramètres sont le nombre de répétitions n et la probabilité p du succès d'une épreuve.
- Dans un arbre de probabilité, toutes les s éries de branches sont identiques.
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Carte mentale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah