Mathématiques 3e - 2021

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Annexes
Scratch
Dossier brevet
Rappels, Index, Compétences
Révisions Genially
Calcul littéral
Plan de travail
Dossier brevet
Retrouvez ici des exercices issus de sujets du brevet pour vous préparer au mieux à cette épreuve.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1[D'après brevet, Antilles Guyane, juin 2019]
Le 1er juillet 2018, la vitesse maximale autorisée sur les routes à double sens de circulation a été abaissée, passant de 90 km/h à 80 km/h.
En 2016, 1 911 personnes ont été tuées sur les routes à double sens de circulation, ce qui représente environ 55 % des décès sur l'ensemble des routes de France.
1.
a. Montrer qu'en 2016, il y a eu environ 3 475 décès sur l'ensemble des routes de France.
b. Des experts ont estimé que la baisse de la vitesse à 80 km/h aurait permis de sauver 400 vies en 2016. De quel pourcentage le nombre de morts sur l'ensemble des routes de France aurait‑il baissé ? Donner une valeur approchée à 0,1 % près.


a. Calculer la moyenne des vitesses des automobilistes contrôlés qui ont dépassé la vitesse maximale autorisée. Donner une valeur approchée à 0,1 km/h près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2[D'après brevet, Métropole La Réunion, juillet 2019]
Voici deux programmes de calcul.

1.
On choisit -5 comme nombre de départ. Calculer, en détaillant
votre démarche, les résultats obtenus lorsqu'on applique les deux programmes.
2.
On appelle \text{A}(x) le résultat du programme 1 en fonction du nombre x choisi au départ.
La fonction \mathrm{B}: x \longmapsto(x-1)(x+2) donne le résultat du programme 2 en fonction du nombre x choisi au départ.
a. Exprimer \text{A}(x) en fonction de x.
b.
Déterminer le nombre que l'on doit choisir au départ pour obtenir 0 avec le programme 1. Détailler le raisonnement.
La fonction \mathrm{B}: x \longmapsto(x-1)(x+2) donne le résultat du programme 2 en fonction du nombre x choisi au départ.
a. Exprimer \text{A}(x) en fonction de x.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3[D'après brevet, Métropole La Réunion, juillet 2019]
Le capitaine d'un navire possède un trésor constitué de 69 perles et 1\,150 pièces d'or.
1. Décomposer 69 et 1\,150 en un produit de facteurs premiers.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4[D'après brevet, Grèce, juin 2019]
\text{TSR} et \text{SPU} sont des triangles rectangles respectivement en \text{T} et en \text{P} tels que \text{TS} = 56\:\text{cm}, \text{SP} = 42\:\text{cm}, \text{RS} = 112\:\text{cm} et \mathrm{\widehat{SUP}} = 30°. Les points \text{T}, \text{S} et \text{P} sont alignés.

1.
Montrer que la mesure de l'angle \mathrm{\widehat{TSR}} est 60°.
2.
Démontrer que les triangles \text{SRT} et \text{SUP} sont semblables.
3.
Calculer la longueur \text{SU}. Détailler le raisonnement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5[D'après brevet, Nouvelle‑Calédonie, mars 2019]

1.
On considère la fonction g représentée précédemment.
a. Donner un antécédent de 4 par la fonction g.
b. Quelle est l'image de 3 par la fonction g ?
c. Compléter le tableau suivant :
a. Donner un antécédent de 4 par la fonction g.
| \bm{x} | -2 | 4 | ||
| \bm{g(x)} | 8 | -2 |
a. Quelle est la nature de la fonction f ?
a. Quelle est la nature de la fonction g ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6[D'après brevet, Métropole, juillet 2019]
Olivia s'est acheté un tableau pour décorer le mur de son salon. Ce tableau est constitué de quatre rectangles identiques nommés
1
, 2
, 3
et 4
dessinés à l'intérieur d'un grand rectangle \text{ABCD} dont l'aire est égale à 1{,}215 m2. 
1.
Compléter les phrases suivantes.
a. Le rectangle est l'image du rectangle par la translation qui transforme \text{C} en \text{E}.
b. Le rectangle par la rotation de centre \text{F} et d'angle 90° dans le sens des aiguilles d'une montre.
c. Le rectangle \text{ABCD} est l'image du rectangle par l'homothétie de centre et de rapport 3. (Il y a plusieurs réponses possibles, une seule est demandée.)
a. Le rectangle
b. Le rectangle
3
est l'image du rectangle c. Le rectangle \text{ABCD} est l'image du rectangle
3
par la symétrie de centre \text{G} (le centre du rectangle).
e. Soit (d) la droite parallèle à la droite \text{(CD)} passant par le milieu du segment \text{[BC]}. Le rectangle
3
est l'image du rectangle 2. Quelle est l'aire du petit rectangle
2
? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7[D'après brevet, Centres Étrangers, juin 2018]
La fleur de sel est la mince couche de cristaux blancs qui se forme et affleure la surface des marais salants. Chaque soir, Jean cueille la fleur de sel à la surface des carreaux. Pour transporter sa récolte, il utilise une brouette comme sur le schéma suivant.

1.
Montrer que cette brouette a un volume de 77 litres.
2.
Sachant qu'un litre de fleur de sel pèse 900 grammes, calculer la masse, en kilogramme, du contenu d'une brouette remplie de fleur de sel.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8[D'après brevet, Nouvelle-Calédonie, décembre 2019]
Dans ce questionnaire à choix multiple, plusieurs réponses sont proposées pour chaque question, mais une seule est exacte. Aucune justification n'est attendue.
1. Une page de roman se lit en moyenne en 1 minute 15 secondes. Quel temps de lecture faudrait‑il pour un roman de 290 pages ?
a. Environ 5 heures
b. Environ 6 heures
c. Environ 7 heures
a. Environ 5 heures
b. Environ 6 heures
c. Environ 7 heures
2. La masse de la planète Neptune est de l'ordre de :
a. 10^{-15} \: \text{kg}
b. 10^{4} \: \text{kg}
c. 10^{26} \: \text{kg}
a. 10^{-15} \: \text{kg}
b. 10^{4} \: \text{kg}
c. 10^{26} \: \text{kg}
a. 2x^{2}-9
b. 2x^{2}-12x+9
c. 4x^{2} -9
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9[D'après brevet, Centres Étrangers, juin 2019]
Dans l'exercice suivant, les figures ne sont pas à l'échelle.
Un décorateur a dessiné une vue de côté d'un meuble de rangement composé d'une structure métallique et de plateaux en bois d'épaisseur 2 cm, illustré par la figure suivante.
Les étages de la structure métallique de ce meuble de rangement sont tous identiques et la figure 2 représente l'un d'entre eux.


On donne :
1. Démontrer que les droites \text{(AB)} et \text{(CD)} sont parallèles.
2.
Montrer par le calcul que \text{AB} = 45 \:\text{cm}.
3.
Calculer la hauteur totale du meuble de rangement.
- \text{OC} = 48 \:\text{cm} ; \text{OD} = 64 \:\text{cm} ; \text{OB} = 27 \:\text{cm} ; \text{OA} = 36 \:\text{cm} et \text{CD} = 80 \:\text{cm} ;
- les droites \text{(AC)} et \text{(CD)} sont perpendiculaires.
1. Démontrer que les droites \text{(AB)} et \text{(CD)} sont parallèles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10[D'après brevet, Métropole, septembre 2019]
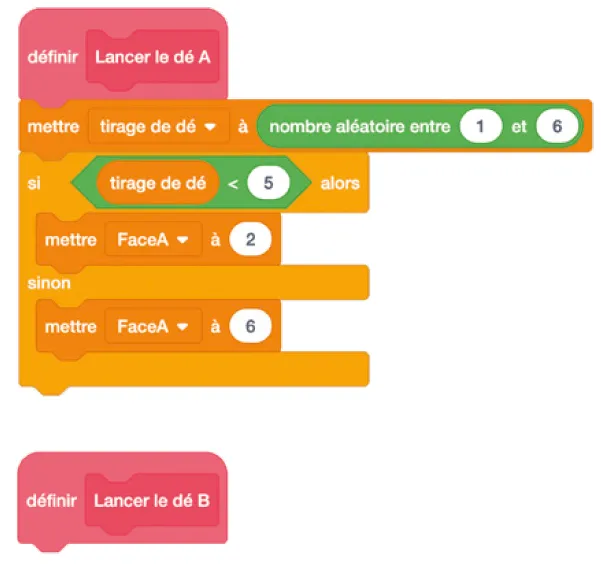
Deux amis Armelle et Basile jouent aux dés en utilisant des dés bien équilibrés mais dont les faces ont été modifiées. Armelle joue avec le dé A et Basile joue avec le dé B. Lors d'un duel, chaque joueur lance son dé et celui qui obtient le plus grand nombre gagne un point.

1.
Un duel peut‑il aboutir à un match nul ?
2. a. Si le résultat obtenu avec le dé A est 2, quelle est la probabilité que Basile gagne un point ?
b. Si le résultat obtenu avec le dé B est 1, quelle est la probabilité qu'Armelle gagne un point ?
On précise que l'expression « nombre aléatoire entre 1 et 6 » renvoie de manière équiprobable un nombre pouvant être 1, 2, 3, 4, 5 ou 6. Les variables « FaceA » et « FaceB » enregistrent les résultats des dés A et B. Par exemple, la variable « FaceA » peut prendre soit la valeur 2 soit la valeur 6, puisque ce sont les seuls nombres présents sur le dé A.
Les variables « Victoire de A » et « Victoire de B » comptent les victoires des joueurs.
a. Lorsqu'on exécute le sous‑programme « Lancer le dé A », quelle est la probabilité que la variable « FaceA » prenne la valeur 2 ?
- Victoire de A = 39 901
- Victoire de B = 20 099
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11[D'après brevet, Polynésie, septembre 2020]
Jean possède 365 albums de BD. Afin de trier les albums de sa collection, il les range par série et classe les séries en trois catégories : franco‑belges, comics et mangas comme dans le tableau suivant.
| Séries franco‑belges | Séries de comics | Séries de mangas |
|---|---|---|
| 23 albums « Astérix » 22 albums « Tintin » 45 albums « Lucky‑Luke » | 35 albums « Batman » 90 albums « Spider‑Man » | 85 albums « One‑Piece » 65 albums « Naruto » |
Il choisit au hasard un album de bandes dessinées parmi tous ceux de sa collection.
1. a. Quelle est la probabilité que l'album choisi soit un album « Lucky‑Luke » ?
b.
Quelle est la probabilité que l'album choisi soit un comics ?
c.
Quelle est la probabilité que l'album choisi ne soit pas un manga ?
1. a. Quelle est la probabilité que l'album choisi soit un album « Lucky‑Luke » ?
2.
Tous les albums de chaque série sont numérotés dans l'ordre de sortie en librairie et chacune des séries est complète du numéro 1 au dernier numéro.
a. Quelle est la probabilité que l'album choisi porte le numéro 1 ?
b.
Quelle est la probabilité que l'album choisi porte le numéro 40 ?
a. Quelle est la probabilité que l'album choisi porte le numéro 1 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12[D'après brevet, Antilles Guyane, septembre 2020]
Voici la série des temps, exprimés en seconde, réalisés par des nageuses lors de la finale du 100 mètres nage libre féminin lors des championnats d'Europe de natation de 2018.
| 53,23 | 54,04 | 53,61 | 54,52 | 53,35 | 52,93 | 54,56 | 54,07 |
1. Quelle est la vitesse moyenne, exprimée en m/s, de la nageuse ayant parcouru les 100 mètres en 52,93 secondes ? Arrondir au dixième près.

4.
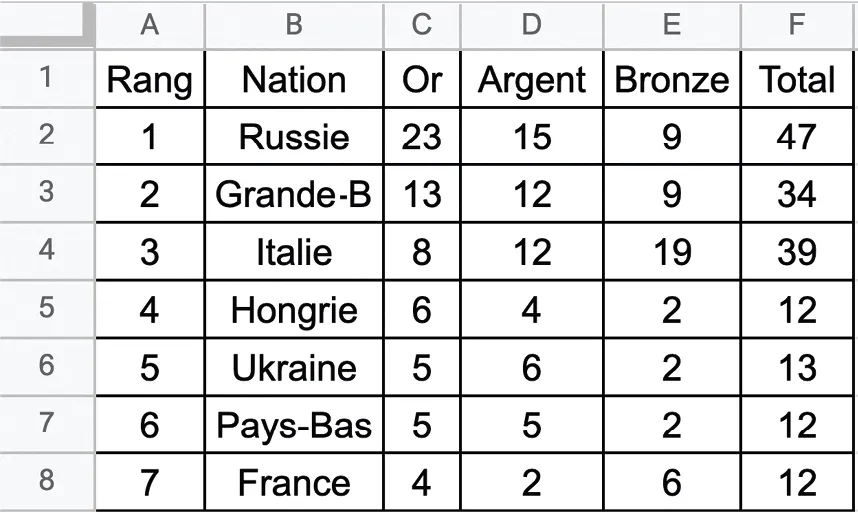
Est-il vrai que plus de 35 % des médailles remportées par la France sont des médailles d'or ?
5.
Quelle formule a‑t‑on pu saisir dans la cellule F2 de cette feuille de calcul, avant qu'elle soit étirée vers le bas jusqu'à la cellule F8 ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille