Mathématiques 3e - 2021
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Annexes
Scratch
Dossier brevet
Rappels, Index, Compétences
Révisions Genially
Calcul littéral
Plan de travail
Chapitre 7
Cours et méthodes
Situations de proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Les ratios
AGénéralités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Soient c et d deux nombres strictement positifs.
On dit que deux nombres positifs a et b sont dans le ratio c pour d, noté «~{c:d}~», si {\frac{a}{c}=\frac{b}{d}}.
On dit que deux nombres positifs a et b sont dans le ratio c pour d, noté «~{c:d}~», si {\frac{a}{c}=\frac{b}{d}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Si a et b sont deux nombres positifs dans le ratio {2:3} alors on peut schématiser la situation comme ceci :

a représente les \frac{2}{5} du total et b les \frac{3}{5}.

a représente les \frac{2}{5} du total et b les \frac{3}{5}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Un pirate et son capitaie se partagent un butin dans le ratio {{\color{#2190A0}3}:\color{#C62A58}4}.
Quand le butin est composé de \color{#5EA85C}7 pièces, le pirate en a \color{#2190A0}3 et le capitaine \color{#C62A58}4. Quand le butin est composé de 350 pièces, le pirate en a 150 (\frac{\color{#2190A0}3}{\color{#5EA85C}7} de 350) et le capitaine en a 200 (\frac{\color{#C62A58}4}{\color{#5EA85C}7} de 350).
Autrement dit, le \mathrm{\color{#2190A0}tiers} du nombre de pièces du pirate est égal au \mathrm{\color{#C62A58}quart} du nombre de pièces du capitaine.
Quand le butin est composé de \color{#5EA85C}7 pièces, le pirate en a \color{#2190A0}3 et le capitaine \color{#C62A58}4. Quand le butin est composé de 350 pièces, le pirate en a 150 (\frac{\color{#2190A0}3}{\color{#5EA85C}7} de 350) et le capitaine en a 200 (\frac{\color{#C62A58}4}{\color{#5EA85C}7} de 350).
Autrement dit, le \mathrm{\color{#2190A0}tiers} du nombre de pièces du pirate est égal au \mathrm{\color{#C62A58}quart} du nombre de pièces du capitaine.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BRatio et tableau de proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Si deux grandeurs sont dans un ratio alors elles sont proportionnelles entre elles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut donc toujours résoudre un problème de ratio en utilisant la notion de proportionnalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On réalise \mathrm{80~mL} de vinaigrette dont le ratio huile : vinaigre est de {3:1}.
On met donc trois fois plus d'huile que de vinaigre. Il nous faudra ainsi \mathrm{60~mL} d'huile et \mathrm{20~mL} de vinaigre.




On met donc trois fois plus d'huile que de vinaigre. Il nous faudra ainsi \mathrm{60~mL} d'huile et \mathrm{20~mL} de vinaigre.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut également étudier le ratio entre trois grandeurs.
Ainsi, on dit que a, b et c sont dans le ratio «~e:f:g~» si \frac{a}{e}=\frac{b}{f}=\frac{c}{g}.
Par exemple, a, b et c sont dans le ratio 2:4:5 si \frac{a}{2}=\frac{b}{4}=\frac{c}{5}.

Ainsi, on dit que a, b et c sont dans le ratio «~e:f:g~» si \frac{a}{e}=\frac{b}{f}=\frac{c}{g}.
Par exemple, a, b et c sont dans le ratio 2:4:5 si \frac{a}{2}=\frac{b}{4}=\frac{c}{5}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthodes
Appliquer un ratio donné
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Yasmine et Mathéo se partagent 21 bonbons dans le ratio 3:4.
Calculer le nombre de bonbons reçus par chacun des enfants.
Calculer le nombre de bonbons reçus par chacun des enfants.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Le nombre total de parts est la somme du nombre de parts de chacun.
- Grâce à la proportion de bonbons attribuée à chacun des enfants, on calcule la quantité de bonbons.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer une quantité à l'aide d'un ratio donné
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Dans une classe de 3e le ratio filles : garçons est de 7:4. Il y a 8 garçons dans cette classe. Calculer le nombre de filles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut schématiser le problème de la manière suivante.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Tableaux de proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Pierre, Paul et Jacques se partagent 120 € dans le ratio 3:4:5.
Quelle quantité d'argent chacun va‑t‑il recevoir ?
Quelle quantité d'argent chacun va‑t‑il recevoir ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- On calcule le nombre total de parts.
- On remplit des tableaux de proportionnalité.
- On les complète en utilisant la méthode de son choix.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
La part totale représentée par le ratio est 3 + 4 + 5 = 12. Quand le premier prend 3 euros, le deuxième prend 4 euros et le troisième 5 euros.
Ainsi le premier reçoit \frac{3}{12}, le deuxième \frac{4}{12} et le dernier \frac{5}{12} du total.

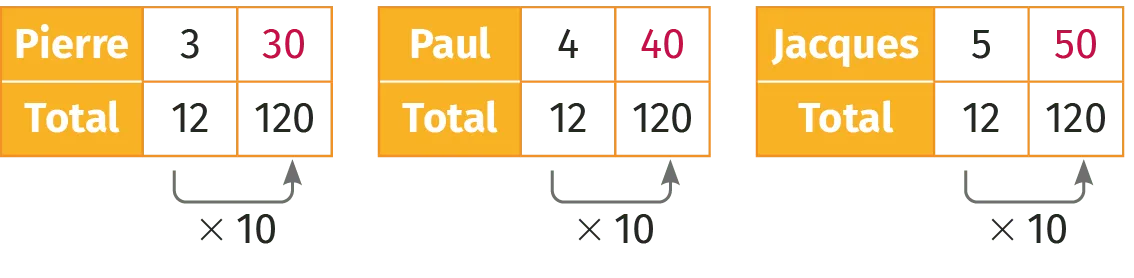 Chacun recevra respectivement 30, 40 et 50 euros.
Chacun recevra respectivement 30, 40 et 50 euros.
Ainsi le premier reçoit \frac{3}{12}, le deuxième \frac{4}{12} et le dernier \frac{5}{12} du total.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Augmentation et réduction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés
1. Augmenter un nombre de \boldsymbol{p~\%} revient à multiplier ce nombre par \boldsymbol{1+\frac{p}{100}}.
2. Diminuer un nombre de \boldsymbol{p~\%} revient à multiplier ce nombre par \boldsymbol{1-\frac{p}{100}}.

2. Diminuer un nombre de \boldsymbol{p~\%} revient à multiplier ce nombre par \boldsymbol{1-\frac{p}{100}}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définitions
1. Dans ce cas, p~\% est appelé le taux d'évolution.
2. Une augmentation de p~\% est modélisée par la fonction linéaire f: x \mapsto\left(1+\frac{p}{100}\right) x.
Une diminution de p~\% est modélisée par la fonction linéaire g: x \mapsto\left(1-\frac{p}{100}\right) x.
On dit que 1+\frac{p}{100} (respectivement 1-\frac{p}{100}) est le coefficient multiplicateur.
3. Dans le cas d'une augmentation, le coefficient multiplicateur qui permet de passer de la quantité initiale à la quantité finale est supérieur à 1 et dans le cas d'une diminution il est inférieur à 1.
2. Une augmentation de p~\% est modélisée par la fonction linéaire f: x \mapsto\left(1+\frac{p}{100}\right) x.
Une diminution de p~\% est modélisée par la fonction linéaire g: x \mapsto\left(1-\frac{p}{100}\right) x.
On dit que 1+\frac{p}{100} (respectivement 1-\frac{p}{100}) est le coefficient multiplicateur.
3. Dans le cas d'une augmentation, le coefficient multiplicateur qui permet de passer de la quantité initiale à la quantité finale est supérieur à 1 et dans le cas d'une diminution il est inférieur à 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Lors des soldes, un blouson voit son prix de 80 € diminué de 40 %.
Le coefficient multiplicateur est 1-\frac{40}{100}=0{,}6.
Le nouveau prix du blouson est donc de {80 \times 0{,}6} soit 48 €.

Le coefficient multiplicateur est 1-\frac{40}{100}=0{,}6.
Le nouveau prix du blouson est donc de {80 \times 0{,}6} soit 48 €.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Attention, les pourcentages ne s'additionnent ou ne se soustraient pas. Lorsque l'on applique successivement deux augmentations, ou deux réductions ou une augmentation suivie d'une réduction, il faut multiplier la quantité initiale par le coefficient qui correspond au produit des coefficients multiplicateurs successifs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Un téléphone portable qui coûtait 240 € subit une réduction de 30 % puis un autre rabais de 20 %.
Pour connaître son nouveau prix, on multiplie le prix initial par {1-\frac{30}{100}=0{,}7}, puis par {1-\frac{20}{100}=0{,}8}.
Comme 0{,}7 \times 0{,}8 = 0{,}56 et {1 - 0{,}56 = 0{,}44}, ce téléphone a donc subi une baisse de 44 % et non une baisse de 50 % comme nous aurions pu l'imaginer.

Pour connaître son nouveau prix, on multiplie le prix initial par {1-\frac{30}{100}=0{,}7}, puis par {1-\frac{20}{100}=0{,}8}.
Comme 0{,}7 \times 0{,}8 = 0{,}56 et {1 - 0{,}56 = 0{,}44}, ce téléphone a donc subi une baisse de 44 % et non une baisse de 50 % comme nous aurions pu l'imaginer.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthodes
Appliquer un taux de réduction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Rachel veut s'offrir une nouvelle robe qui coûte 35 €. Elle possède un code permettant d'obtenir une réduction de 15 %. Combien va lui coûter sa robe après réduction ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Diminuer un prix de p~\% revient à le multiplier par 1-\frac{p}{100}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouver une donnée
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Le prix d'un smartphone a augmenté de 25 %. Il coûte 224 €. Quel était son ancien prix ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- On détermine le coefficient multiplicateur associé à l'augmentation subie.
- On résout l'équation obtenue.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer un taux d'évolution
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Le prix d'un abonnement à une salle de sport est passé de 150 € en 2019 à 154,50 € en 2020. Calculer le taux d'évolution appliqué.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Pour déterminer le taux d'évolution, on se ramène d'abord au coefficient multiplicateur associé : 1+\frac{p}{100} dans le cas d'une augmentation et 1-\frac{p}{100} dans le cas d'une diminution.
- On met en équation et on résout.
- On déduit la valeur de p grâce au coefficient multiplicateur obtenu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
On cherche p tel que 150 \times\left(1+\frac{p}{100}\right)=154{,}50 c'est‑à‑dire {1+\frac{p}{100}=\frac{154{,}50}{150}} donc 1+\frac{p}{100}=1{,}03.
Or, le coefficient multiplicateur 1{,}03 correspond à une augmentation de 3 %. Le prix de l'abonnement a donc augmenté de 3 %.
Or, le coefficient multiplicateur 1{,}03 correspond à une augmentation de 3 %. Le prix de l'abonnement a donc augmenté de 3 %.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
