Indiquer si la proposition est vraie ou fausse.

1. 4 n'admet que deux diviseurs

Vraie

Fausse

2. 1\,137 est un nombre premier

Vraie

Fausse

3. 1 est un nombre premier

Vraie

Fausse

4. 2 est le seul nombre premier pair

Vraie

Fausse

5. 21 et 49 n'ont pas de diviseurs communs

Vraie

Fausse

6. 49 est un diviseur de 7

Vraie

Fausse

7. 72 a exactement cinq diviseurs

Vraie

Fausse

1. Choisir les bons mots afin que les phrases soient correctes.
a. Le nombre 648 estn'est pas premier car il estn'est pas pas divisible par 2.

b. Le nombre 972 n'est pas premierpair car il est un multiplediviseur de 2.

c. La fraction \frac{648}{972} estn'est pas irréductible car on peut la simplifier par un 25.

2. Compléter les pointillés afin d'obtenir la décomposition en un produit de facteurs premiers des nombres 648 et 972.
a. 648=

\times

b. 972=

\times

3. En déduire la forme irréductible de la fraction ci-dessous en recopiant et complétant les pointillés pour justifier les étapes.

\frac{648}{972}=\frac{ \ldots \ldots \ldots}{ \ldots \ldots \ldots}=\frac{ \ldots \ldots \ldots }{ \ldots \ldots \ldots }

1. Compléter l'égalité suivante traduisant la division euclidienne de 1\,512 par 21.
2. Décomposer 1\,512 en un produit de facteurs premiers.

3. Décomposer 720 en un produit de facteurs premiers.

4. Utiliser les résultats précédents pour rendre irréductible la fraction \frac{720}{1512}.

1. Associer les nombres de gauche à leur décomposition dans la colonne de droite

2. Utiliser les résultats précédents pour recopier et compléter les pointillés et donner ainsi la forme irréductible des fractions suivantes.
a. \frac{108}{135}=\frac{\ldots \ldots \ldots}{\ldots \ldots \ldots}=\frac{\ldots \ldots \ldots}{\ldots \ldots \ldots}

b. \frac{3\,822}{9\,240}=\frac{\ldots \ldots \ldots}{\ldots \ldots \ldots}=\frac{\ldots \ldots \ldots}{\ldots \ldots \ldots}

1. Déterminer la décomposition en un produit de facteurs premiers des nombres suivants.
a. 2\,000

b. 2\,001

2. Que peut-on en déduire concernant les deux nombres 2\,000 et 2\,001 ?

3. Que peut-on en déduire pour la fraction \frac{2\,000}{2\,001} ?
Justifier en utilisant les questions 1. et 2.

1. Décomposer les nombres 1\,756 et 1\,317 en un produit de facteurs premiers.
a. 1\,756

b. 1\,317

2. Un fleuriste a reçu 1\,756 roses et 1\,317 pivoines. Il va réaliser des bouquets identiques en utilisant toutes les fleurs.
a. En utilisant la question 1. , donner le nombre maximal de bouquets identiques que le fleuriste peut confectionner.

b. Combien de roses comporte chaque bouquet ?

c. Combien de pivoines comporte chaque bouquet ?

3. Une rose coûte 2,30 € et une pivoine 1,25 €. Quel est le prix du bouquet ?

1. Décomposer 5\,148 en un produit de facteurs premiers.

2. Décomposer 1\,386 en un produit de facteurs premiers.

3. En déduire la forme irréductible de \frac{5\,148}{1\,386}

\frac{7}{26}

\frac{26}{7}

\frac{2^{2} \times 3^{2} \times 11 \times 13}{2 \times 3^{2} \times 7 \times 11}

\frac{52}{14}

On considère le programme suivant.
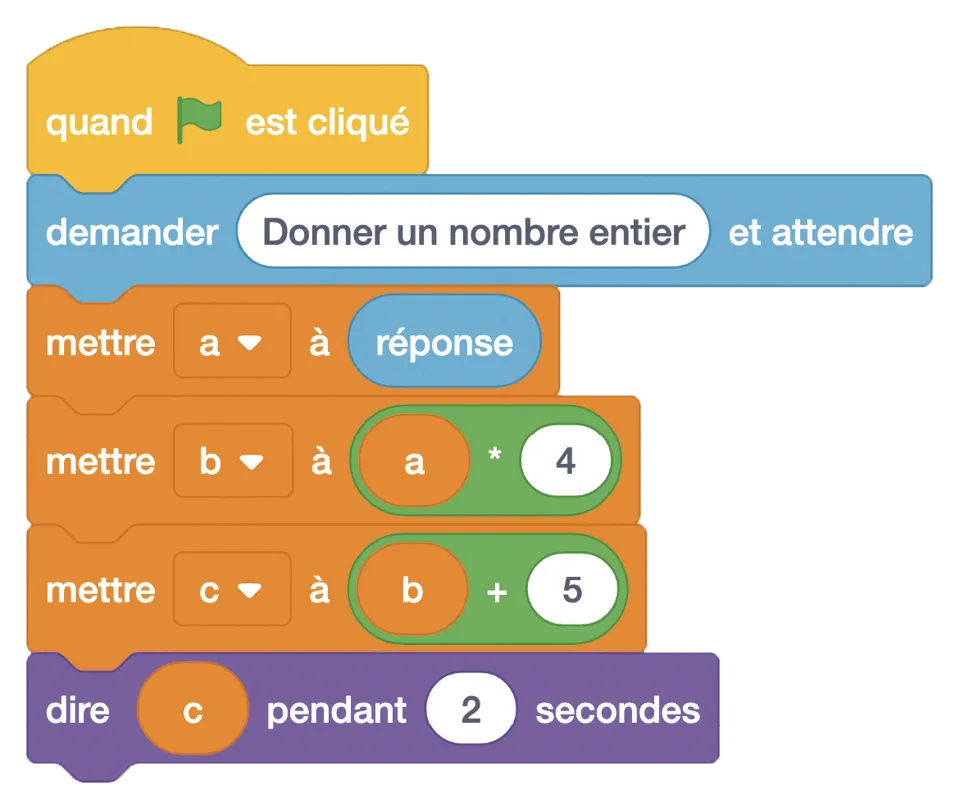
1. Quel est le résultat si le nombre donné est 3 ?

2. Quel est le résultat si le nombre donné est 12 ?

3. Marie affirme que le résultat obtenu peut être un multiple de 2. Est-ce vrai ? Le démontrer.

On considère l'expression n^{2}+n+41 avec n un nombre entier positif. Samia affirme que cette expression donne toujours un nombre premier. A-t-elle raison ? Justifier.