Mathématiques Terminale Bac Pro - Cahier
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 7
Applications directes
Vecteurs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer les coordonnées d'un point dans l'espace.

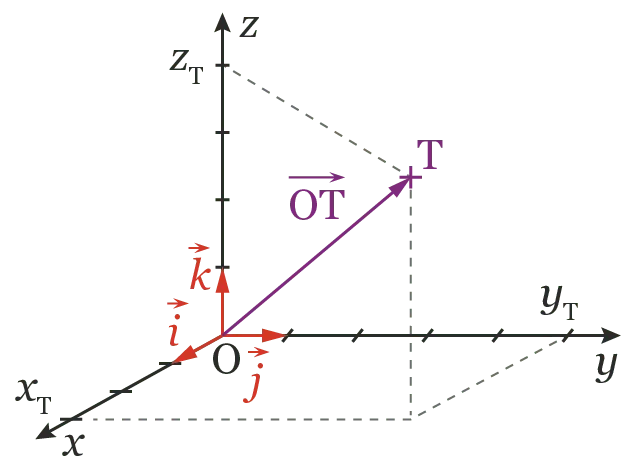
Dans un repère (\mathrm{O} \: ; \vec{i}, \vec{j}, \vec{k}) le point \text{T} est repéré par ses coordonnées \left(x_{\mathrm{T}} ; y_{\mathrm{T}} ; z_{\mathrm{T}}\right).
- x_{\mathrm{T}} correspond à la valeur sur l'axe des abscisses (\mathrm{O} x) ;
- y_{\mathrm{T}} correspond à la valeur sur l'axe des ordonnées (\mathrm{O} y) ;
- z_{\mathrm{T}} correspond à la valeur sur l'axe des cotes (\mathrm{O} z).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Identifier des vecteurs égaux, opposés ou colinéaires.

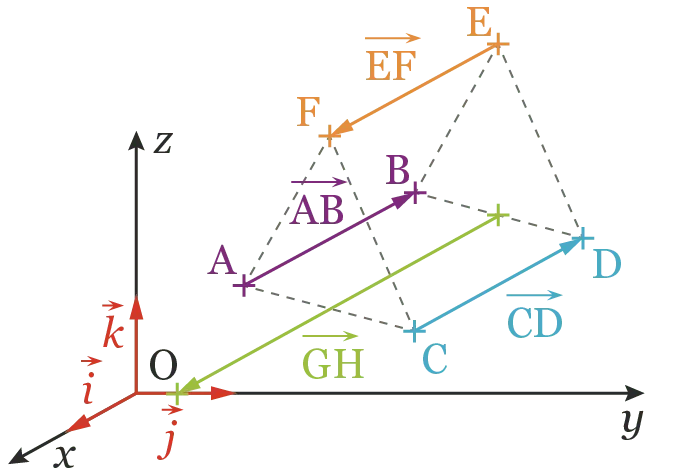
- Deux vecteurs \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{CD}} sont égaux si :
- les droites (\text{AB}) et (\text{CD}) sont parallèles (même direction) ;
- ils sont de même sens ;
- ils ont la même norme.
- Deux vecteurs \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{CD}} sont également égaux s'ils ont les mêmes coordonnées.
- Deux vecteurs \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{EF}} sont opposés s'ils ont la même direction et la même norme mais un sens opposé.
- Deux vecteurs \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{GH}} sont colinéaires s'ils ont la même direction mais pas forcément le même sens ni la même norme. On peut alors écrire {\overrightarrow{\mathrm{AB}}=k \times \overrightarrow{\mathrm{GH}}} avec k un réel.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exprimer la somme de deux vecteurs.
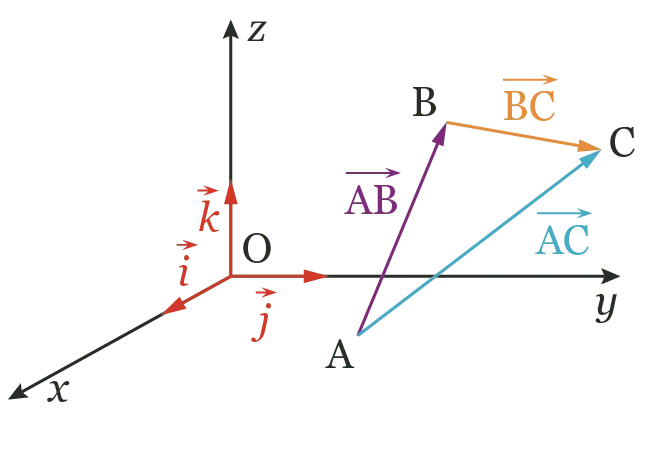
Relation de Chasles :
\overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{BC}} = \overrightarrow{\mathrm{AC}}.

Méthode du parallélogramme : \overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{AD}} = \overrightarrow{\mathrm{AC}}.

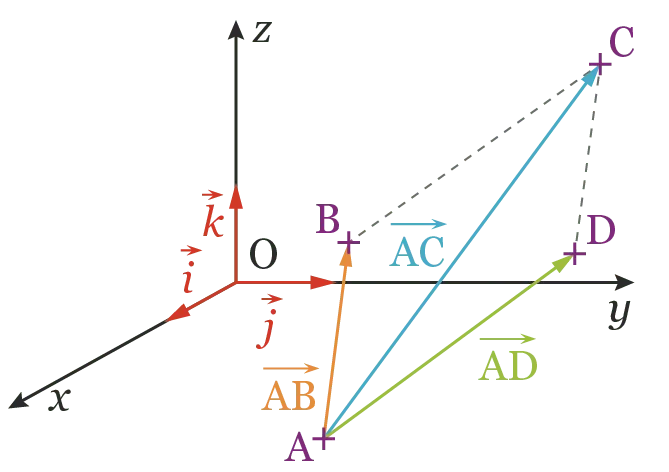


Méthode du parallélogramme : \overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{AD}} = \overrightarrow{\mathrm{AC}}.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer les coordonnées d'un vecteur dans l'espace et calculer sa norme.


- Le vecteur \overrightarrow{\mathrm{AB}} est défini par les points \text{A} et \text{B}.
- Les coordonnées du vecteur \overrightarrow{\mathrm{AB}} sont {\overrightarrow{\mathrm{AB}}\left(\begin{array}{c} x_{\mathrm{B}}-x_{\mathrm{A}} \\ y_{\mathrm{B}}-y_{\mathrm{A}} \\ z_{\mathrm{B}}-z_{\mathrm{A}} \end{array}\right)}.
- La norme du vecteur \overrightarrow{\mathrm{AB}} est {\|\overrightarrow{\mathrm{AB}}\|=\sqrt{\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^{2}+\left(z_{\mathrm{B}}-z_{\mathrm{A}}\right)^{2}}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Mise en pratique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCM
Une ou plusieurs bonnes réponses possibles.L'espace est rapporté au repère orthonormé (\mathrm{O} \: ; \vec{i}, \vec{j}, \vec{k}) d'unité graphique 1 cm.

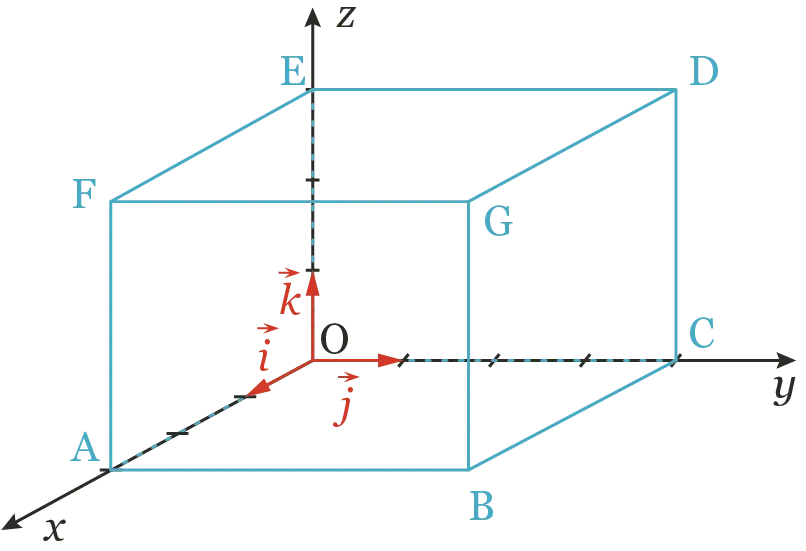
1. Les coordonnées de \text{D} sont :
2. Les coordonnées du vecteur \overrightarrow{\mathrm{OC}} sont :
3. Les coordonnées du vecteur \overrightarrow{\mathrm{AD}} sont :
2. Les coordonnées du vecteur \overrightarrow{\mathrm{OC}} sont :
3. Les coordonnées du vecteur \overrightarrow{\mathrm{AD}} sont :
4. La norme du vecteur \overrightarrow{\mathrm{BF}} est :
5. Les vecteurs \overrightarrow{\mathrm{BG}} et \overrightarrow{\mathrm{OE}} sont :
6. \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BE}}=\ldots
7. \overrightarrow{\mathrm{GF}}+\overrightarrow{\mathrm{GD}}=\ldots
5. Les vecteurs \overrightarrow{\mathrm{BG}} et \overrightarrow{\mathrm{OE}} sont :
6. \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BE}}=\ldots
7. \overrightarrow{\mathrm{GF}}+\overrightarrow{\mathrm{GD}}=\ldots
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème
Une barre cylindrique en acier de 4 m de longueur et de 0,20 m de diamètre a une masse de 1 000 kg. Elle est maintenue en équilibre horizontal par deux élingues représentées par les segments [\mathrm{AC}] et [\mathrm{BC}].
On donne les coordonnées, dans un repère orthonormé (\mathrm{O} \: ; \vec{i}, \vec{j}, \vec{k}), de \mathrm{G}(2 \: ; 2 \: ; 4), le centre de gravité de la barre, ainsi que des points \mathrm{A}(2 \: ; 0,5 \: ; 4,1) et \mathrm{B}(2 \: ; 3,5 \: ; 4,1), les points de fixation des élingues sur la barre. L'unité graphique est le mètre.
On sait, de plus, que le point \text{C} se situe à la verticale du point \text{G} à une distance de 1,50 m.
On donne les coordonnées, dans un repère orthonormé (\mathrm{O} \: ; \vec{i}, \vec{j}, \vec{k}), de \mathrm{G}(2 \: ; 2 \: ; 4), le centre de gravité de la barre, ainsi que des points \mathrm{A}(2 \: ; 0,5 \: ; 4,1) et \mathrm{B}(2 \: ; 3,5 \: ; 4,1), les points de fixation des élingues sur la barre. L'unité graphique est le mètre.
On sait, de plus, que le point \text{C} se situe à la verticale du point \text{G} à une distance de 1,50 m.

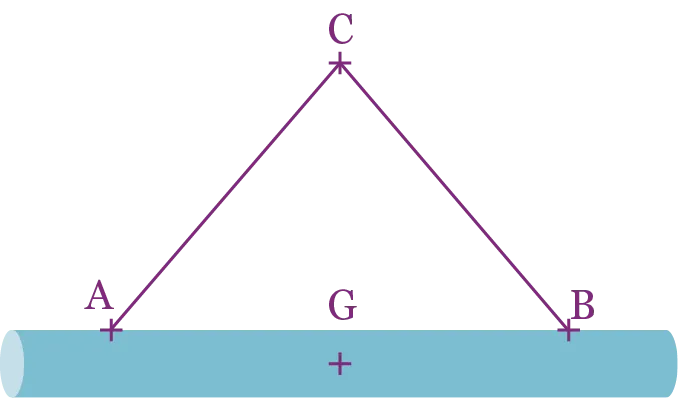
1. Donner les coordonnées du point \text{C}.
2. Calculer les coordonnées des vecteurs \overrightarrow{\mathrm{AC}} et \overrightarrow{\mathrm{BC}}.
3. Calculer, à 0,01 m près, la longueur des élingues correspondant aux segments [\mathrm{AC}] et [\mathrm{BC}].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Réviser les notions de ce chapitre grâce à cette activité interactive.
Pour une utilisation optimale, réaliser l'activité en plein écran.
Pour une utilisation optimale, réaliser l'activité en plein écran.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
