Mathématiques 4e - Cahier d'exercices - 2022
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d’équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Chapitre 11
Exercices de bilan
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15QCM[Rais.1 - Rais.5]
Cocher la (ou les) bonne(s) réponse(s).
1. Dans la figure suivante, les trois droites bleues sont parallèles entre elles.
 On peut donc dire que :
On peut donc dire que :

2. Dans la figure suivante, on sait que \frac{\mathrm{HI}}{\mathrm{HK}}=\frac{\mathrm{HN}}{\mathrm{HL}} et que \frac{\mathrm{HJ}}{\mathrm{HK}} \neq \frac{\mathrm{HM}}{\mathrm{HL}}.
 Alors on peut dire que :
Alors on peut dire que :

3. Soit \text{PRS} un triangle tel que \text{T} appartient au côté \text{[PR]} et \text{V} appartient au côté \text{[PS]}.
Si \frac{\mathrm{PT}}{\mathrm{PR}}=\frac{\mathrm{PV}}{\mathrm{PS}}, alors on peut dire que :
4. Dans le triangle \text{TRI}, \text{A} appartient au segment \text{[TR]} et \text{B} appartient au segment \text{[TI]}.
On a l'égalité \frac{\mathrm{TR}}{\mathrm{TA}}=\frac{\mathrm{TI}}{\mathrm{TB}}.
Quelles sont les droites parallèles ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16[Ch.1 - Mod.4 - Com.4]
Lucie souhaite connaître la hauteur de son immeuble. À 45 mètres de celui-ci se trouve un arbre de 8 mètres de haut. Elle recule de 5 mètres depuis l'arbre afin que son regard soit aligné avec la cime de l'arbre et le haut de l'immeuble. Dans la figure suivante, qui n'est pas à l'échelle, on a symbolisé la façade de l'immeuble par le segment \text{[IM]}, l'arbre par le segment \text{[AR]} et le regard de Lucie par le point \text{L}. On estime que le regard de Lucie se trouve à \text{1,60~m} du sol.
1. Indiquer les différentes mesures, en mètre, sur la figure suivante.
2. Déterminer la hauteur \text{IM} de l'immeuble, au dixième de mètre près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Copie d'élève[Mod.4 - Rais.4 - Rais.5]
En feuilletant le cahier d'exercices de son petit
frère, Anas lit une de ses résolutions de problème.
On a \frac{2}{5}=\frac{4}{10} donc \frac{\text{DA}}{\text{DB}}=\frac{\text{DE}}{\text{BC}}.
Ainsi, \text{(DE)} et \text{(BC)} sont parallèles.
Ainsi, \text{(DE)} et \text{(BC)} sont parallèles.

Anas lui affirme que son raisonnement est faux. Pourquoi ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18[Rais.6]
Voici un dont les instructions ont été mélangées. Le travail porte sur l'étude d'un triangle \text{PAR} dans lequel \text{C} est un point de \text{[PA]} et \text{S} est un point de \text{[PR]}.

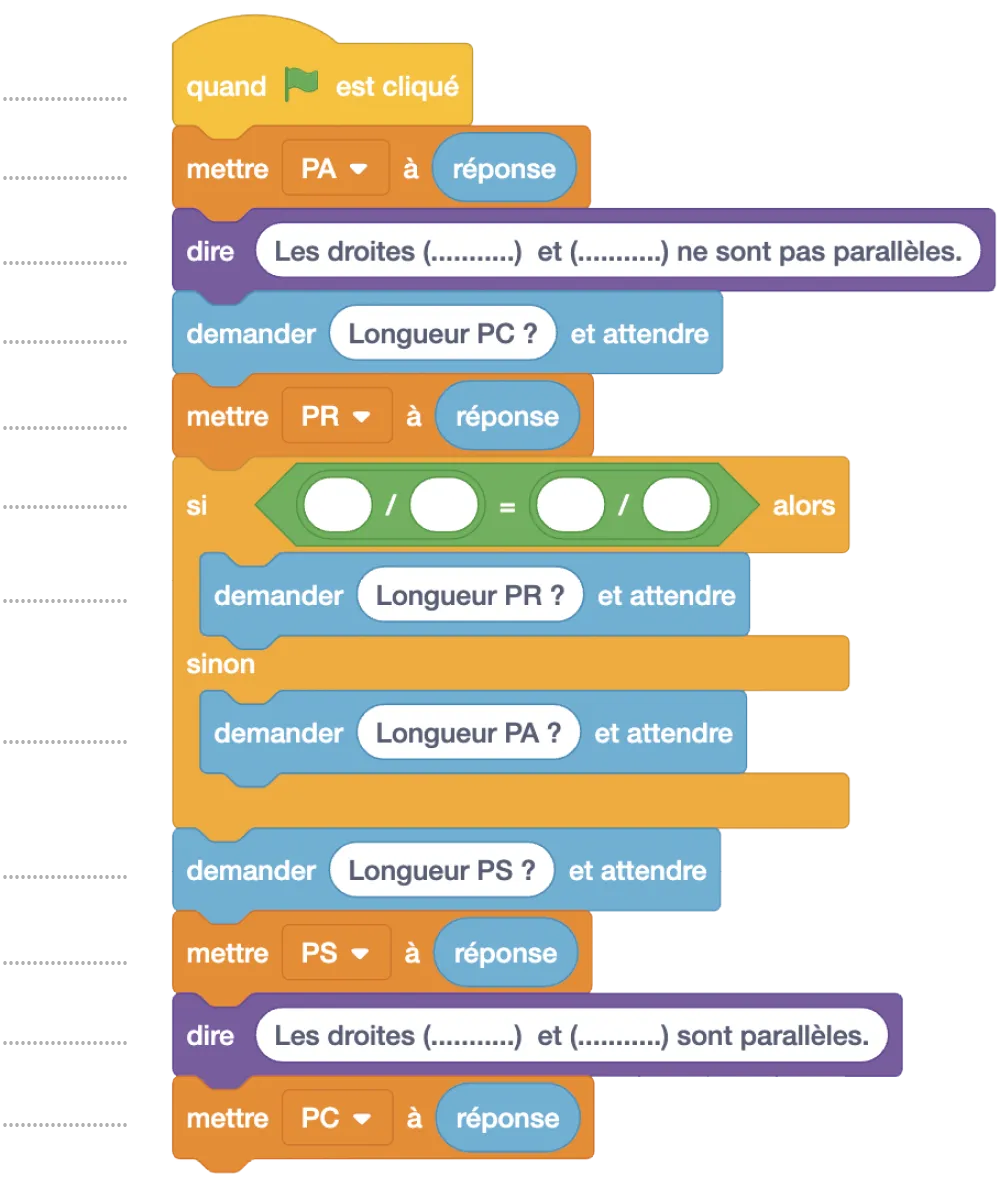
PA
PC
PR
PS
4. Un utilisateur entre les données suivantes : \text{PA = 5}, \text{PC = 2}, \text{PS = 3} et \text{PR = 6}. Que va afficher le programme ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19[Mod.4 - Rais.3]
Un étendoir à linge en parapluie a une structure composée de quatre triangles identiques au triangle \text{ABC} présenté sur la figure suivante.Chaque triangle accueille huit cordes tendues, toutes parallèles et espacées sur la structure d'une longueur \text{BD = 6~cm}. On sait de plus que \text{AB = AC = 48~cm} et que \text{BC = 64~cm}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
