Mathématiques 4e - Cahier d'exercices - 2022
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d’équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Chapitre 8
Exercices de bilan
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19QCM[Mod.7 - Cal.3 - Com.1]
Cocher la (ou les) bonne(s) réponse(s).1. On lance un dé équilibré à six faces numérotées de \text{1} à \text{6}. La probabilité d'obtenir un nombre supérieur ou égal à \text{5} est égale à :
2. On lance une pièce de monnaie équilibrée. L'événement « Obtenir face. » est un événement :
3. On considère un événement \text{A} tel que \text{P}(\text{A})=0,27. Alors :
4. On choisit au hasard l'une des couleurs d'un stylo quatre couleurs (rouge, bleu, noir ou vert). La probabilité d'obtenir du vert est égale à :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20[Mod.7 - Cal.4 - Rais.4]
On écrit chacune des huit lettres du mot
« VACANCES » sur des papiers tous indiscernables au toucher et on pioche l'un de ces papiers au hasard. On s'intéresse à la lettre obtenue.1. Est-ce une situation d'équiprobabilité ? Justifier.
2. Sélectionner les bonnes affirmations en bleu, puis calculer les probabilités demandées.
a. \text{A} : « Obtenir la lettre N. » est un événement / et \text{P}(\text{A}) =
b. \text{B} : « Obtenir une consonne. » est un événement / et \text{P}(\text{B}) =
c. \text{C} : « Obtenir une lettre. » est un événement / et \text{P}(\text{C}) =
d. \text{D} : « Obtenir la lettre A ou la lettre E. » et l'événement \mathrm{B} sont des événements / . Ainsi, on peut également noter l'événement \text{D} :
et \text{P}(\text{D}) =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21[Cal.5 - Cal.4]
On considère une expérience aléatoire dont les
issues sont équiprobables.1. Rappeler la formule permettant de calculer la probabilité d'un événement \text{A} en fonction du nombre d'issues favorables à \text{A} et du nombre total d'issues de l'univers.

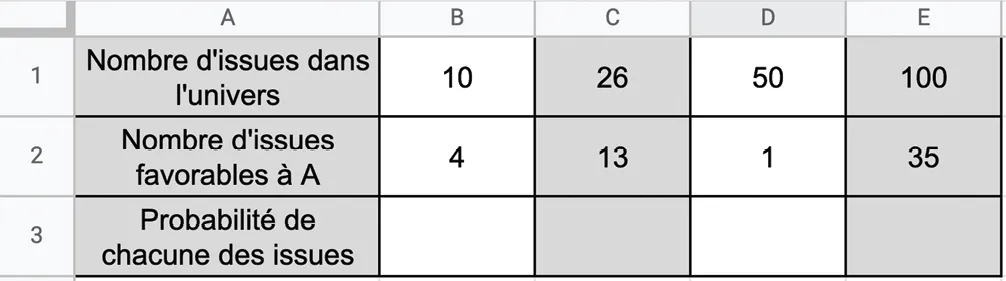
Quelle formule faut-il saisir dans la cellule B3 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22[Cal.5 - Cal.4 - Rep.8]
On considère une expérience aléatoire dont les
issues sont équiprobables.
1. Rappeler la formule permettant de calculer la probabilité d'un événement \overline{\mathrm{A}} en fonction de celle de \text{A}.
2. À l'aide d'une feuille de calcul, on souhaite pouvoir compléter le tableau suivant. La cellule D1 devra contenir un nombre aléatoire entre \text{0} et \text{1}.

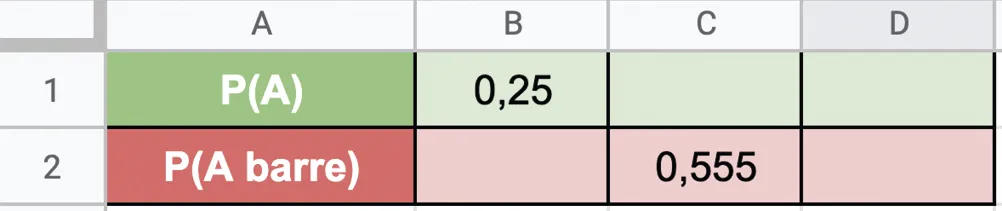
Donner les formules à saisir en cellule :
a. B2 :
b. C1 :
1. Rappeler la formule permettant de calculer la probabilité d'un événement \overline{\mathrm{A}} en fonction de celle de \text{A}.


Donner les formules à saisir en cellule :
a. B2 :
c. D1 :
d. D2 :
3. Compléter les cellules du tableur avec les résultats que l'on doit obtenir si la cellule D1 affiche \text{0,2819}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23[Mod.7 - Cal.4]
On attribue à chaque élève d'une classe de 25 élèves un numéro correspondant à sa position dans l'ordre alphabétique et on considère alors .

2. a. Quelle est la probabilité que l'élève choisi soit le n°77 ?
b. Que peut-on dire de cet événement ?
3. Quelle est la probabilité que l'élève choisi ait un numéro pair ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24[Mod.7 - Cal.3 - Rais.5]
Amélie et Raphaël jouent avec un dé à six faces qui n'est
pas équilibré. Tous les deux effectuent des tests pour déterminer la probabilité de chacune de ses faces.Raphaël a trouvé les probabilités suivantes.
| Issue | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Probabilité | 0,2 | 0,1 | 0,2 | 0,1 | 0,2 | 0,1 |
Amélie a trouvé les probabilités suivantes.
| Issue | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Probabilité | 0,25 | 0,25 | 0,25 | 0,1 | 0,1 | 0,1 |
Expliquer pourquoi, sans avoir le dé en main, on sait que les deux amis ont tort.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25[Mod.7 - Cal.4 - Rais.4]
Une urne contient sept boules vertes, quatre boules rouges, trois boules bleues et deux boules jaunes, toutes indiscernables au toucher. On pioche au hasard l'une de ces boules et on regarde sa couleur.
1. Est-ce une situation d'équiprobabilité ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26[Mod.7 - Com.1 - Cal.4]
On dispose d'un sac jaune et d'un sac bleu. On place dans le sac jaune des papiers jaunes et des bleus dans le sac bleu, tous étant indiscernables au toucher.


On pioche, sans remise, un papier bleu puis un jaune puis enfin un papier bleu et on effectue l'opération indiquée. On s'intéresse au résultat de cette opération. Par exemple, si on pioche :


1. Donner un événement : a. impossible :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
