Mathématiques 1re Spécialité
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 8
Entrainement 2
Étude des fonctions trigonométriques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour chacune des fonctions suivantes définies et dérivables sur \mathbb{R}, donner l'expression de la fonction dérivée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
[Calculer.] f(x)=2 \cos (x)+x
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
[Calculer.]
g(x)=x^{2} \sin (x)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
[Calculer.]
h(x)=x \sin (-3 x+4)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour chacune des fonctions suivantes défi nies sur \text{I} \subset[-\pi \: ; \pi], déterminer les ensembles de définition et de dérivabilité puis déterminer l'expression de la fonction dérivée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
[Calculer.]f(x)=\dfrac{1}{\sin (x)}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
[Calculer.]
g(x)=\dfrac{\sin (x)}{\cos (x)}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
[Calculer.] h(x)=\cos (-2 x+4) \sin (-2 x+4)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
[Calculer.]
k(x)=\cos (3 x-2) \sin (-3 x+2)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
[Calculer.]
Pour un devoir sur table, Valentine a oublié sa calculatrice et doit absolument savoir quel est le plus grand nombre entre \cos(2) et \cos(3) . Comment peut-elle le savoir ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
[Calculer.]
Julia, une camarade de Valentine, est dans le même cas qu'elle et a également oublié sa calculatrice pour le devoir sur table. Pour répondre à une question, elle doit savoir quel est le plus grand nombre entre \sin(4) et \sin(7). Comment peut-elle le savoir ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
[Représenter.] On considère l'inéquation \sin (x)>\dfrac{1}{3} pour x \in[-\pi \: ; \pi].
1. a. En utilisant une fenêtre graphique adaptée, tracer à la calculatrice la courbe du sinus et une droite permettant de résoudre graphiquement cette inéquation.
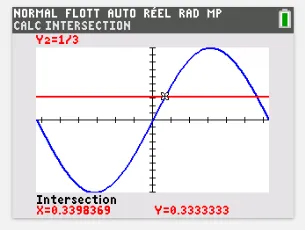
b. Faire un croquis à main levée du graphe obtenu.
Cliquez pour accéder à une correction
b. Faire un croquis à main levée du graphe obtenu.
Cliquez pour accéder à une zone de dessin
2. Résoudre graphiquement cette inéquation.
3. Dessiner l'ensemble solution sur le cercle trigonométrique.
3. Dessiner l'ensemble solution sur le cercle trigonométrique.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
[Calculer.] On considère la fonction f : x \mapsto \sin (4 x-1) définie sur \mathbb{R}. 1. Calculer f^{\prime}(x) pour tout x \in \mathbb{R}.
2. La dérivée seconde de f est la dérivée de la dérivée de f . On la note f '' .
Démontrer que f'' est définie sur \mathbb{R} par f^{\prime \prime}(x)=-16 \sin (4 x-1).
Aide
On commencera par calculer f '(x) puis il faudra dériver f'.
3. Pour tout x \in \R, calculer f^{\prime\prime}(x) + 16f(x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
[Calculer.] On considère les fonctions g : x \mapsto 3 \cos (3 x+4) et h : x\mapsto-25 \sin (5 x-2) définies sur \mathbb{R}. 1. Trouver une fonction \text{G} vérifiant pour tout x \in \mathbb{R}, \mathrm{G}^{\prime}(x)=g(x).
2. Trouver une fonction \text{H} vérifiant pour tout x \in \mathbb{R}, \text{H}''(x) = h(x) . On obtient \text{H}'' en dérivant deux fois de suite la fonction \text{H.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
[Calculer.]
On considère la fonction f : x \mapsto 4 \cos (x)+(\cos (x))^{2} définie sur \mathbb{R} . 1. Justifier que f est dérivable et montrer que, pour tout x \in \mathbb{R}, f^{\prime}(x)=-2 \sin (x) \times(2+\cos (x)).
2. En déduire les variations de f sur [0\: ; 2 \pi].
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
