Sommaire
Mes pages
N° Page
ouverture
p. 1-11
Algèbre
Analyse
Géométrie
Probabilités et statistiques
Annexes
/ 353
Page précédente
Chapitre 8
Synthèse

Exercices de synthèse - Objectif BAC

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Différenciation
Parcours 1 : exercices
40
 ;
45
 ;
53
 ;
56
 et
62
Parcours 2 : exercices
42
 ;
58
 ;
63
 ;
74
 et
76
Parcours 3 : exercices
48
 ;
49
 ;
64
 et
75
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
66
 [Communiquer.]
Résoudre dans \mathbb{R} l'équation (2 \cos (x)-\sqrt{2})\left(\sin ^{2}(x)-1\right)=0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
67
 [Communiquer.]
Résoudre dans ]-\pi \: ; \pi ] l'inéquation (2 \sin (x)-\sqrt{2})(1-2 \cos (x)) \geqslant 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
68
 [Communiquer.]
On considère la fonction h : x \mapsto \dfrac{x}{2}+\sin (x) définie sur \mathbb{R} . 1. Calculer h'(x) pour tout x \in \mathbb{R}.

2. Donner le tableau de variations de h sur l'intervalle [-\pi \: ; \pi].

3. Pourquoi peut-on connaître les variations de h sur \mathbb{R} tout entier ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
69
 [Chercher.]
Pour chacune des fonctions définies sur \mathbb{R} par les expressions suivantes, conjecturer la période à l'aide de la calculatrice puis démontrer cette conjecture. 1. f : x \mapsto \sin ^{2}(2 x)

2. g : x \mapsto 4 \sin (x) \times \sin \left(\dfrac{x}{3}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
70
PYTHON
[Modéliser.]
Soit y un nombre réel donné. L'algorithme suivant permet de résoudre numériquement l'équation \sin(x) = y avec x \in\left[-\dfrac{\pi}{2} \: ; \dfrac{\pi}{2}\right]. 

from math import* 

def dichotomie_sin(y, p):
  if(y > ...) or (y < ...):
    return(False)
  else:
    a = —pi/2
    b = pi/2
    while b — a >= p:
      res = (a + b)/2
      if sin(res) > y:
        ... = ...
      else:
        ... = ...
    return(res)

On utilise une méthode de dichotomie qui permet de trouver une solution approchée avec une précision donnée (notée p dans le programme).
1. Comment compléter la ligne 4 ?

2. On va chercher à compléter le programme fourni.
a. À quoi correspondent les variables \bf{a} et \bf{b} ?

b. Que teste-t-on ligne 9 ?

c. Compléter alors le programme fourni.
Cliquez pour accéder à la correction






Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.







71
 [Communiquer.]


On considère la fonction f définie sur \mathbb{R} par f(x)=\sin \left(\dfrac{x}{a}\right)+\cos \left(\dfrac{x}{b}\right) où a et b sont deux nombres réels quelconques.


On note k le plus petit multiple commun à a et b .










1. Démontrer que 2k\pi est une période de f.















2. En déduire alors une période de la fonction g définie sur \mathbb{R} par g(x)=\sin \left(\dfrac{x}{2}\right)+\cos \left(\dfrac{x}{3}\right).











Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.







72
 [Calculer.]


Le but de ce problème est d'étudier la fonction f : x \mapsto \cos ^{2}(x) définie sur \mathbb{R}.










1. La fonction f est-elle paire ? Impaire ? Ni l'un ni l'autre ?






2. Montrer que f est \pi-périodique.






3. Justifier que f est dérivable sur \mathbb{R} puis calculer f'(x).















4. Déterminer les variations de f sur \left[-\dfrac{\pi}{2} \: ; \dfrac{\pi}{2}\right].






5. Cela suffit-il à connaître les variations de f sur tout \mathbb{R} ?











Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.







73
EN PHYSIQUE
[Modéliser.]











En physique, les oscillations harmoniques (pendules, ressorts, ondes, etc.) sont décrites par des fonctions de la forme \cos (\omega t+\phi) ou \sin (\omega t+\phi) où \omega est appelé pulsation et \phi est la phase.
















Fonctions trigonométriques























1. La courbe ci-dessus représente l'oscillation f : t \mapsto \cos (4 t). Déterminer par lecture graphique la période \text{T} de ce signal. Vérifier ce résultat par le calcul.







2. Conjecturer une formule reliant la pulsation \omega et la période \text{T.}






3. Tester cette conjecture sur les oscillations suivantes. 

a. g(t)=\cos (6 t+2)
















b. h(t)=\cos \left(\dfrac{t}{2}\right)







4. Démontrer la conjecture.











Placeholder pour Pendule de Foucault au Panthéon, Paris. Un grand pendule oscille au-dessus d'un sol en marbre. Des visiteurs observent.Pendule de Foucault au Panthéon, Paris. Un grand pendule oscille au-dessus d'un sol en marbre. Des visiteurs observent.







Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.







74
 [Communiquer.] 



Le but de ce problème est l'étude de la fonction f : x \mapsto \sin (x)+\cos (x) définie sur \mathbb{R}.










1. Pourquoi peut-on restreindre l'étude de cette fonction à l'intervalle [-\pi \: ; \pi] ?






2. Calculer la dérivée de f.






3. Résoudre l'inéquation \cos(x) > \sin(x) sur [-\pi \: ; \pi].















4. En déduire le tableau de variations de f .




    
Cliquez pour accéder à une zone de dessin

        

    

    


5. Déterminer la valeur maximale que peut prendre f .











Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.







75
EN PHYSIQUE
[Modéliser.] 












On suspend une masse m à un ressort. On note y la hauteur relative de la masse. La valeur y = 0 correspond à l'équilibre lorsque la masse est immobile. On amène la masse à 10 cm de hauteur puis on la lâche. On suppose qu'il n'y a pas d'amortissement des oscillations. Les oscillations pour t \geqslant 0 (t en seconde) sont données par y( t ) = 10\cos(3t) . On remarque qu'au temps t_0 = 0, on a y(t_0) = 10.
















Fonctions trigonométriques



Placeholder pour Photo : règle en bois mesurant un ressort métallique. Expérience scientifique de physique.Photo : règle en bois mesurant un ressort métallique. Expérience scientifique de physique.























1. Pour quel temps t_1 la masse va passer pour la première fois par sa position d'équilibre y = 0 ?






2. Pour quel temps t_2 la masse va repasser pour la deuxième fois par sa position d'équilibre ?















3. Quelle est la période des oscillations de la masse ?






4. Quelle sera la hauteur maximale de la masse ? Et la hauteur minimale ?






Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.







76
EN PHYSIQUE
[Chercher.] 




En physique, lors de l'étude des oscillateurs harmoniques d'ordre 2, on cherche des fonctions f qui vérifient (\mathrm{E}) : f^{\prime \prime}(t)+\omega^{2} f(t)=0 pour tout t \geqslant 0 avec \omega \in \mathbb{R} (la fonction f'' est obtenue en dérivant deux fois la fonction f).







Placeholder pour Photo : circuit électrique avec bobines toroïdale et cylindrique en cuivre, connectées par fils sur support bois.Photo : circuit électrique avec bobines toroïdale et cylindrique en cuivre, connectées par fils sur support bois.



Fonctions trigonométriques - circuit éléctrique



Exemple d'oscillateur harmonique d'ordre 2 : oscillations libres dans un circuit LC en électricité.












1. Soit a_1 un réel.


a. Montrer que f_{1} : t \mapsto \cos \left(\omega t+a_{1}\right) vérifie \text{(E).}






b. Déterminer une valeur possible de a_1 telle que f_{1}(0)=0.















2. Soit a_2 un réel.


a. Montrer que f_{2} : t \mapsto \sin \left(\omega t+a_{2}\right) vérifie \text{(E).}






b. Déterminer une valeur possible de a_2 telle que f_{2}(0)=\dfrac{1}{2}.













Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.







77
 [Chercher.]











On considère une sphère \mathcal{S} de rayon 1 centrée en \text{O} dans un repère de l'espace (\mathrm{O} ; \mathrm{I}, \mathrm{J}, \mathrm{K}). On considère un point \text{A} de la sphère appartenant au plan \text{(OIK)} et on note \theta=\widehat{\mathrm{IOA}}. On note \mathcal{C} le cylindre inscrit dans la sphère, passant par \text{A} et orienté par \text{(OK).}
















Fonctions trigonométriques























1. Expliquer pourquoi on peut considérer que \theta \in\left[0 \: ; \dfrac{\pi}{2}\right].






2. Exprimer le volume \mathrm{V}_{\mathrm{C}}(\theta) du cylindre \mathcal{C} en fonction de \theta (on commencera par exprimer la hauteur et le rayon de ce cylindre).






3. On note \text{V}_\text{S} le volume de la sphère \mathcal{S}. Montrer que, pour tout \theta \in\left[0 \: ; \dfrac{\pi}{2}\right], on a \mathrm{V}_{\mathrm{S}}>\mathrm{V}_{\mathrm{C}}(\theta). Pouvait-on prévoir cette inégalité ?



Aide
\cos (a) \times \sin (a)=\dfrac{1}{2} \sin (2 a)














4. On souhaite savoir quelles sont les dimensions que le cylindre doit avoir pour que son volume soit égal à la moitié du volume de la sphère.


a. Proposer une méthode afin de connaître une valeur de \theta à 0{,}1 près, vérifiant la condition voulue. Donner alors les dimensions du cylindre.






b. Est-il possible d'obtenir des dimensions du cylindre permettant que sa surface latérale soit la moitié de la surface de la sphère (on pourra trouver une valeur exacte de \theta) ?







Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

  
Club de Maths


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.



78
ÉNIGME
 



Pourquoi peut-on dire que, pour les fonctions sinus et cosinus, enlever \dfrac{\pi}{2} revient à dériver ?







Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.







79
ALGO
 


Nous allons étudier le périmètre des polygones réguliers inscrits dans le cercle trigonométrique. On note \text{P}_n le périmètre du polygone à n côtés pour n \geqslant 3 et \alpha_n la mesure de l'angle \widehat{\mathrm{AOB}}, où \text{O} est le centre du cercle et \text{A} et \text{B} sont deux sommets consécutifs de ce polygone.









Fonctions trigonométriques














1. Calculer \text{P}_3 et \text{P}_4.






2. À présent, on considère que n \geqslant 5.


a. Quelle est la valeur de \alpha_n ?






b. Calculer alors la longueur \text{AB} en fonction de n .






c. En déduire une expression de \text{P}_n.






d. Cette formule fonctionne-t-elle quand n = 4 ? n = 3 ?






e. La formule fonctionne-t-elle pour le cas limite n = 2 ?















3. On cherche à présent à faire les calculs à l'aide d'un tableur. Quelle formule doit-on rentrer dans la cellule B4 ?







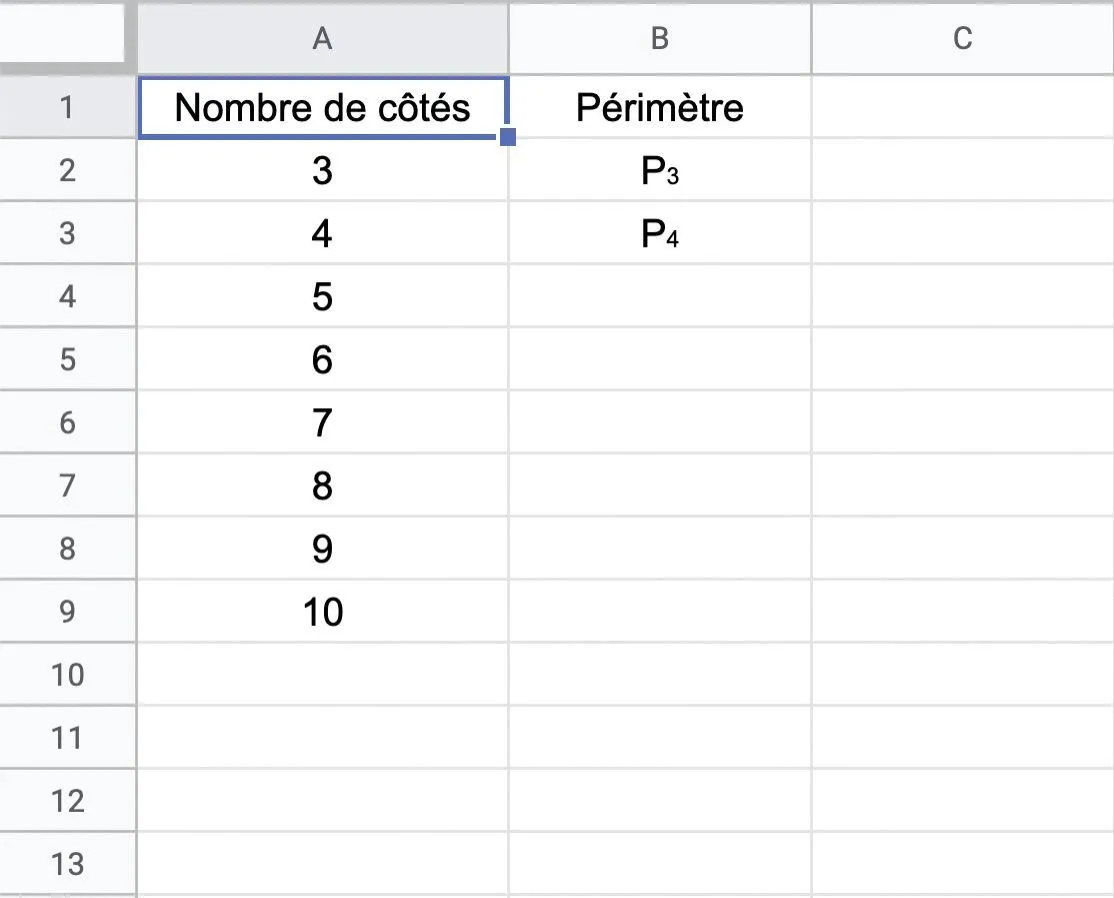
Placeholder pour Tableau listant le nombre de côtés et le périmètre de polygones.Tableau listant le nombre de côtés et le périmètre de polygones.










4. Compléter le tableau à l'aide des questions précédentes. Que remarque-t-on quand on augmente fortement le nombre de côtés ? Comment l'expliquer ?








Remarque


On pourra aussi consulter le 
TP/TICE p. 212
 pour voir d'autres méthodes.



Histoire des maths


Ce type de méthode a été utilisé par Archimède afin de proposer un encadrement de \pi. À l'aide de deux polygones réguliers de même nombre de côtés, l'un inscrit et l'autre circonscrit au cercle trigonométrique, il a obtenu l'encadrement \dfrac{223}{71} \leqslant \pi \leqslant \dfrac{22}{7}  Pour cela, il n'a bien entendu pas utilisé les sinus et cosinus, juste des figures précises et des calculs utilisant les fractions. L'inégalité a été obtenue à l'aide d'un polygone régulier à 96 côtés !










Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.







80
DÉFI
 


Les propositions suivantes sont-elles vraies ou fausses ? Justifier.










1. Si une fonction dérivable en tout point de son ensemble de définition est paire, alors sa fonction dérivée est impaire.















2. Si une fonction dérivable en tout point de son ensemble de définition est impaire, alors sa fonction dérivée est paire.









Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.



81
CASSE-TÊTE
 


Trouver le maximum et le minimum de la fonction h : x \mapsto 4 \sin (x)-\sin ^{2}(x) sur \mathbb{R} .







Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.



82
DÉFI
 


Soit n \in \mathbb{N} . Lorsqu'une fonction f est définie et dérivable n fois sur \mathcal{D}_f, on note f' sa dérivée et f'' sa dérivée seconde qui est la dérivée de la dérivée.
On note f^{(3)} la dérivée troisième de f et f^{(3)}=(f'')'.
On peut continuer comme ça en notant f^{(n)} la dérivée de f^{(n-1)}, et ainsi de suite.


On peut alors établir que, pour tout x \in \mathcal{D}_f et pour a \in \mathcal{D}_f fixé :



f(x) \approx f(a)+(x-a) f^{\prime}(a)+\dfrac{(x-a)^{2}}{2 !} f^{\prime \prime}(a)+\dfrac{(x-a)^{3}}{3 !} f^{(3)}(a)+\ldots+\dfrac{(x-a)^{n}}{n !} f^{(n)}(a)



Que donne cette formule avec les fonctions cosinus et sinus lorsque a = 0 et n = 4 ?





Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

  
  

	

			
Exercices transversaux en lien avec ce chapitre :
			

				
        
17
 
        
18
 
        
24
 
        
25
 
        
28
 
        
			

	





Page suivante
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille