1. Donner la valeur exacte de g(-3) puis une valeur approchée au centième près.

2. a. Justifier que g est dérivable et calculer g'(x) pour tout x \in \mathbb{R} .

b. En déduire le tableau de variations de g sur \mathbb{R} .



3. On donne le tableau de signes de g(x) sur \mathbb{R}. On admet que g est continue sur son ensemble de définition.


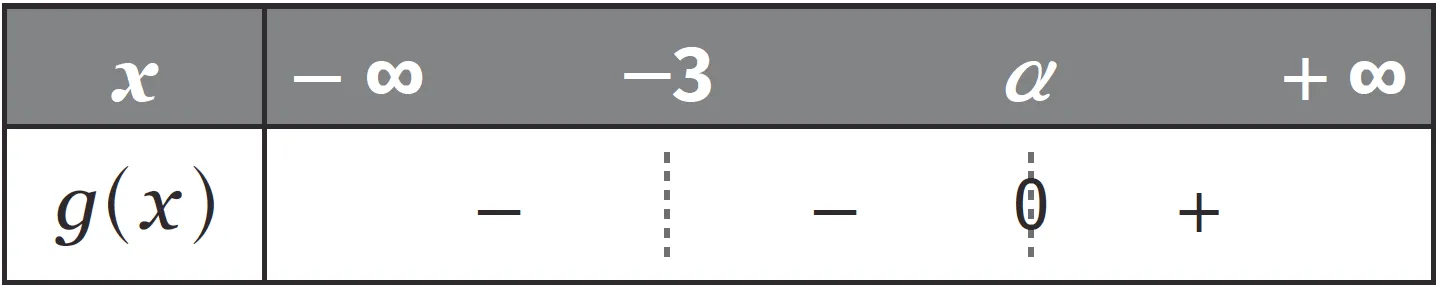
a. En utilisant les fonctionnalités de la calculatrice, déterminer une valeur approchée de \alpha à 10^-2 près.

b. Donner une expression de \mathrm{e}^{\alpha-4} sous forme fractionnaire en fonction de \alpha.

4. Soit f la fonction définie sur \mathbb{R} par f(x)=x^{2}-x^{2} e^{x-4}. a. Démontrer que, pour tout x \in \mathbb{R} , f'(x)=-x g(x).

b. En déduire les variations de f sur \mathbb{R}.

c. Démontrer que le maximum de f sur [0\: ;+\infty[ est \dfrac{\alpha^{3}}{\alpha+2}.

Partie A :
Voici deux courbes \mathcal{C}_1 et \mathcal{C}_2 qui donnent pour deux personnes \text{P}_1 et \text{P}_2 de corpulences différentes la concentration \text{C} d'alcool dans le sang (taux d'alcoolémie) en fonction du temps t après ingestion de la même quantité d'alcool. L'instant t = 0 correspond au moment où les deux individus ingèrent l'alcool. \text{C} est exprimée en gramme par litre et t en heure.
Définition : La corpulence est le nom scientifique correspondant au volume du corps.


1. La fonction \text{C} est définie sur l'intervalle [0\: ; +\infty[ et on note \text{C}' sa fonction dérivée. À un instant t positif ou nul, la vitesse d'apparition d'alcool dans le sang est donnée par \text{C}'(t). À quel instant cette vitesse est-elle maximale ?

2. On dit souvent qu'une personne de faible corpulence subit plus vite les effets de l'alcool. Sur le graphique précédent, identifier la courbe correspondant à la personne la plus corpulente. Justifier le choix effectué.

3. Une personne à jeun absorbe de l'alcool. On admet que la concentration \text{C} d'alcool dans son sang peut être modélisée par la fonction f définie sur [0\: ; +\infty[ par f(t) = \text{A}t e^{-t} , où \text{A} est une constante positive qui dépend de la corpulence et de la quantité d'alcool absorbée.

a. On note f' la fonction dérivée de la fonction f . Déterminer f '(0) en fonction de \text{A}.

b. L'affirmation suivante est-elle vraie ?
« À quantité d'alcool absorbée égale, plus \text{A} est grand, plus la personne est corpulente. »

Partie B : Un cas particulier
Paul, étudiant de 19 ans de corpulence moyenne et jeune conducteur, boit deux verres de rhum. La concentration \text{C} d'alcool dans son sang est modélisée en fonction du temps t , exprimé en heure, par la fonction f définie sur [0\: ;+\infty[ par f(t)=2 t \mathrm{e}^{-t}.

1. Étudier les variations de f sur l'intervalle [0\: ;+\infty[.

2. À quel instant la concentration d'alcool dans le sang de Paul est-elle maximale ? Quelle est alors sa valeur ? Arrondir à 10^-2 près.

3. À l'aide d'une calculatrice, qu'observe-t-on lorsque le temps t devient de plus en plus grand ? Interpréter le résultat dans le contexte de l'exercice.

4. Paul veut savoir au bout de combien de temps il peut prendre sa voiture. On rappelle que la législation autorise une concentration maximale d'alcool dans le sang de 0,2 g·L^–1 pour un jeune conducteur.
On admet qu'il existe deux nombres réels t_1 et t_2 tels que f(t_{1})=f(t_{2})=0{,}2. À l'aide d'une calculatrice, quelle durée minimale Paul doit-il attendre avant de pouvoir prendre le volant en toute légalité ? Donner le résultat arrondi à la minute la plus proche.

Partie A : À l'aide de la calculatrice, conjecturer les abscisses des points respectifs de \mathcal{C}_f et \mathcal{C}_g où les deux courbes semblent admettre deux tangentes communes.

Partie B : Dans cette partie, on admet l'existence de ces tangentes communes. On note \mathcal{D} l'une d'entre elles. Cette droite est tangente à la courbe \mathcal{C}_f au point \text{A} d'abscisse a et tangente à la courbe \mathcal{C}_g au point \text{B} d'abscisse b .

1. a. Exprimer en fonction de a le coefficient directeur de la tangente à la courbe \mathcal{C}_f au point \text{A .}

b. Exprimer en fonction de b le coefficient directeur de la tangente à la courbe \mathcal{C}_g au point \text{B .}

c. En déduire que b = -a .

2. Démontrer que le réel a est solution de l'équation 2(x-1) e^{x}+1=0.

Partie C : On considère la fonction \varphi définie sur \mathbb{R} par \varphi(x)=2(x-1) e^{x}+1.

1. a. Calculer la dérivée de la fonction \varphi, puis étudier son signe.

b. Étudier les variations de la fonction \varphi sur \mathbb{R}. Préciser la valeur de \varphi(0).

2. a. À l'aide de la calculatrice, conjecturer le nombre de solutions de l'équation \varphi(x)=0 dans \mathbb{R}.

b. On note \alpha la solution négative de l'équation \varphi(x)=0 et \beta la solution positive de cette équation. À l'aide de la calculatrice, donner ces valeurs arrondies au centième.

Partie D : Dans cette partie, on démontre l'existence de ces tangentes communes, que l'on a admise dans la partie B.
On note \text{E} le point de la courbe \mathcal{C}_f d'abscisse \alpha et \text{F} le point de la courbe \mathcal{C}_g d'abscisse -\alpha (\alpha est le nombre réel défini dans la partie C).

1. Démontrer que la droite (\text{EF}) est tangente à la courbe \mathcal{C}_f au point \text{E.}

2. Démontrer que (\text{EF}) est tangente à \mathcal{C}_g au point \text{F.}

Une entreprise spécialisée est chargée par l'office de tourisme d'une station de ski de la conception d'un panneau publicitaire ayant la forme d'une piste de ski.
Afin de donner des informations sur la station, une zone rectangulaire est insérée sur le panneau comme indiqué sur la figure ci-après.


Le panneau est découpé dans une plaque rectangulaire de 2 mètres sur 1 mètre. Il est modélisé ci-dessous dans un repère orthonormé (\mathrm{O} ; \vec{i}, \vec{j}) et l'unité choisie est le mètre.

Soit x un nombre réel appartenant à l'intervalle [0\: ; 2]. On note :

• \text{M} le point de la courbe \mathcal{C} de coordonnées (x\: ; \mathrm{e}^{-x^{2}}) ;
• \text{N} le point de coordonnées (x\: ; 0) ;
• \text{P} le point de coordonnées (0\: ; \mathrm{e}^{-x^{2}}) ;
• \text{A}(x) l'aire du rectangle \text{ONMP.}

1. Justifier que pour tout nombre réel x de l'intervalle [0\: ; 2], on a : \mathrm{A}(x)=x \mathrm{e}^{-x^{2}}.

2. On admet que si une fonction u est dérivable sur un intervalle \text{I}, alors (\text{e}^u)'=u'\text{e}^u. Déterminer la position du point \text{M} sur la courbe \mathcal{C} pour laquelle l'aire du rectangle \text{ONMP} est maximale.

3. Le rectangle \text{ONMP} d'aire maximale obtenu à la question 2. doit être peint en bleu. Déterminer, en m² et à 10^-2 près, la mesure de la surface à peindre en bleu.

1. Donner, par lecture graphique, le signe de f(x) selon les valeurs de x .

2. On désigne par \text{F} la fonction définie sur \mathbb{R} telle que \text{F}' = f sur \mathbb{R}.
a. À l'aide de la courbe \mathcal{C}, déterminer \text{F}'(0) et \text{F}'(-2).

b. L'une des courbes \mathcal{C}_1, \mathcal{C}_2, \mathcal{C}_3 est la courbe représentative de la fonction \text{F.}
Déterminer laquelle en justifiant l'élimination des deux autres.

Partie A : Étude de la fonction f
1. Justifier que, pour tout x \in \mathbb{R} :-e^{-x} \leqslant f(x) \leqslant 3 e^{-x}.

2. Démontrer que, pour tout x \in \mathbb{R}, f^{\prime}(x)=\mathrm{e}^{-x}(2 \cos x-1) où f' est la fonction dérivée de la fonction f .

3. Dans cette question, on étudie la fonction f sur l'intervalle [-\pi \: ; \pi].
a. Déterminer le signe de f'(x) pour x appartenant à l'intervalle [-\pi \: ; \pi].

b. En déduire les variations de f sur [-\pi \: ; \pi].

Partie B : Aire du logo
On note \mathcal{C}_f et \mathcal{C}_g les représentations graphiques des fonctions f et g dans un repère orthonormé (\mathrm{O} ; \vec{i}, \vec{j}). L'unité graphique est de 2 centimètres. L'unité d'aire est alors égale à 4 cm² (1 u.a. = 4 cm²). Ces deux courbes sont tracées ci-dessous.


1. Étudier la position relative de la courbe \mathcal{C}_f par rapport à la courbe \mathcal{C}_g sur \mathbb{R} .

2. Soit \text{H} la fonction définie sur \mathbb{R} par \mathrm{H}(x)=\left(-\dfrac{\cos x}{2}-\dfrac{\sin x}{2}-1\right) \mathrm{e}^{-x}.
Démontrer que, pour tout réel x, la fonction dérivée de \text{H} est la fonction x \mapsto(\sin x+1) \mathrm{e}^{-x}.

3. On note \mathcal{D} le domaine délimité par la courbe \mathcal{C}_f, la courbe \mathcal{C}_g et les droites d'équation x=-\dfrac{\pi}{2} et x=\dfrac{3\pi}{2}. On admet que l'aire du domaine \mathcal{D} correspond à \mathrm{H}\left(\dfrac{3 \pi}{2}\right)-\mathrm{H}\left(-\dfrac{\pi}{2}\right).
Calculer, en unité d'aire, l'aire du domaine \mathcal{D}, puis en donner une valeur approchée à 10^-2 près en cm².

On considère la fonction f définie sur \mathbb{R} par f(x)=(x+2) e^{-x}. On note \mathcal{C} la courbe représentative de la fonction f dans un repère orthogonal. 1. Étude de la fonction f
a. Déterminer les coordonnées des points d'intersection de la courbe \mathcal{C} avec les axes du repère.

b. Étudier les variations de f sur \mathbb{R}.

2. Calcul d'une valeur approchée de l'aire sous une courbe
On note \mathcal{D} le domaine compris entre l'axe des abscisses, la courbe \mathcal{C} et les droites d'équation x = 0 et x = 1 . On approche l'aire du domaine \mathcal{D} en calculant une somme d'aires de rectangles.

a. Dans cette question, on découpe l'intervalle [0\: ; 1] en quatre intervalles de même longueur :

• sur l'intervalle \left[0 \:; \dfrac{1}{4}\right], on construit un rectangle de hauteur f(0) ;
• sur l'intervalle \left[\dfrac{1}{4} \:; \dfrac{1}{2}\right], on construit un rectangle de hauteur f\left(\dfrac{1}{4}\right) ;
• sur l'intervalle \left[\dfrac{1}{2}\: ; \dfrac{3}{4}\right], on construit un rectangle de hauteur f\left(\dfrac{1}{2}\right) ;
• sur l'intervalle \left[\dfrac{3}{4}\: ; 1\right], on construit un rectangle de hauteur f\left(\dfrac{3}{4}\right).

Cette construction est illustrée ci-dessous.


L'algorithme ci-dessous permet d'obtenir une valeur approchée \text{S} de l'aire du domaine \mathcal{D} en ajoutant les aires des quatre rectangles précédents.

\boxed{ \begin{array} { l } \text {S} \leftarrow 0 \\ \text{Pour k variant de 0 à 3 :} \\ \quad \text{S} \leftarrow \text{S}+\dfrac{1}{4} f\left(\dfrac{\text{k}}{4}\right)\\ \text {Fin pour} \end{array} }

Donner une valeur approchée à 10^-3 près du résultat affiché par cet algorithme.

b. Dans cette question, \text{N} est un nombre entier strictement supérieur à 1. On découpe l'intervalle [0 \:; 1] en \text{N} intervalles de même longueur. Sur chacun de ces intervalles, on construit un rectangle en procédant de la même manière qu'à la question 2. a. Modifier l'algorithme précédent afin qu'il calcule en sortie la somme des aires des \text{N} rectangles ainsi construits.

3. Calcul de la valeur exacte de l'aire sous une courbe
Soit g la fonction définie sur \mathbb{R} par g(x)=(-x-3) e^{-x}.

a. Démontrer que f est la fonction dérivée de g sur \mathbb{R}.

b. On admet que la valeur exacte de l'aire \mathcal{A} du domaine \mathcal{D}, exprimée en unités d'aire, est égale à g(1) - g(0) . Calculer cette aire.

c. Donner une valeur approchée à 10^-3 près de l'erreur commise en remplaçant \mathcal{A} par la valeur approchée trouvée au moyen de l'algorithme de la question 2. a., c'est-à-dire l'écart entre ces deux valeurs.

On considère la courbe \mathcal{C} d'équation y = e^x , tracée ci-dessous. On note \mathcal{D} la droite d'équation y = e \times x . Démontrer que la droite \mathcal{D} est tangente à la courbe \mathcal{C} en son point d'abscisse 1.

Le plan est muni d'un repère orthonormé (\mathrm{O} ; \vec{i}, \vec{j}).
On considère une fonction f dérivable sur l'intervalle [-3\: ; 2]. On dispose des informations suivantes :

• f(0)=-1 ;
• la dérivée f' de la fonction f admet la courbe représentative \mathcal{C}' ci-dessous.

Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse et justifier la réponse.

1. Pour tout réel x de l'intervalle [-3\:;-1] : f^{\prime}(x) \leqslant 0.

2. La fonction f est croissante sur l'intervalle [-1\:;2].

3. Pour tout réel x de l'intervalle [-3\:;2], f(x) \geqslant -1.

4. Soit \mathcal{C} la courbe représentative de la fonction f .
La tangente à la courbe \mathcal{C} au point d'abscisse 0 passe par le point de coordonnées (1\: ; 0).