Mathématiques Cycle 4
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 7
Exercices
Je résous des problèmes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49Le vivant et les longueurs.

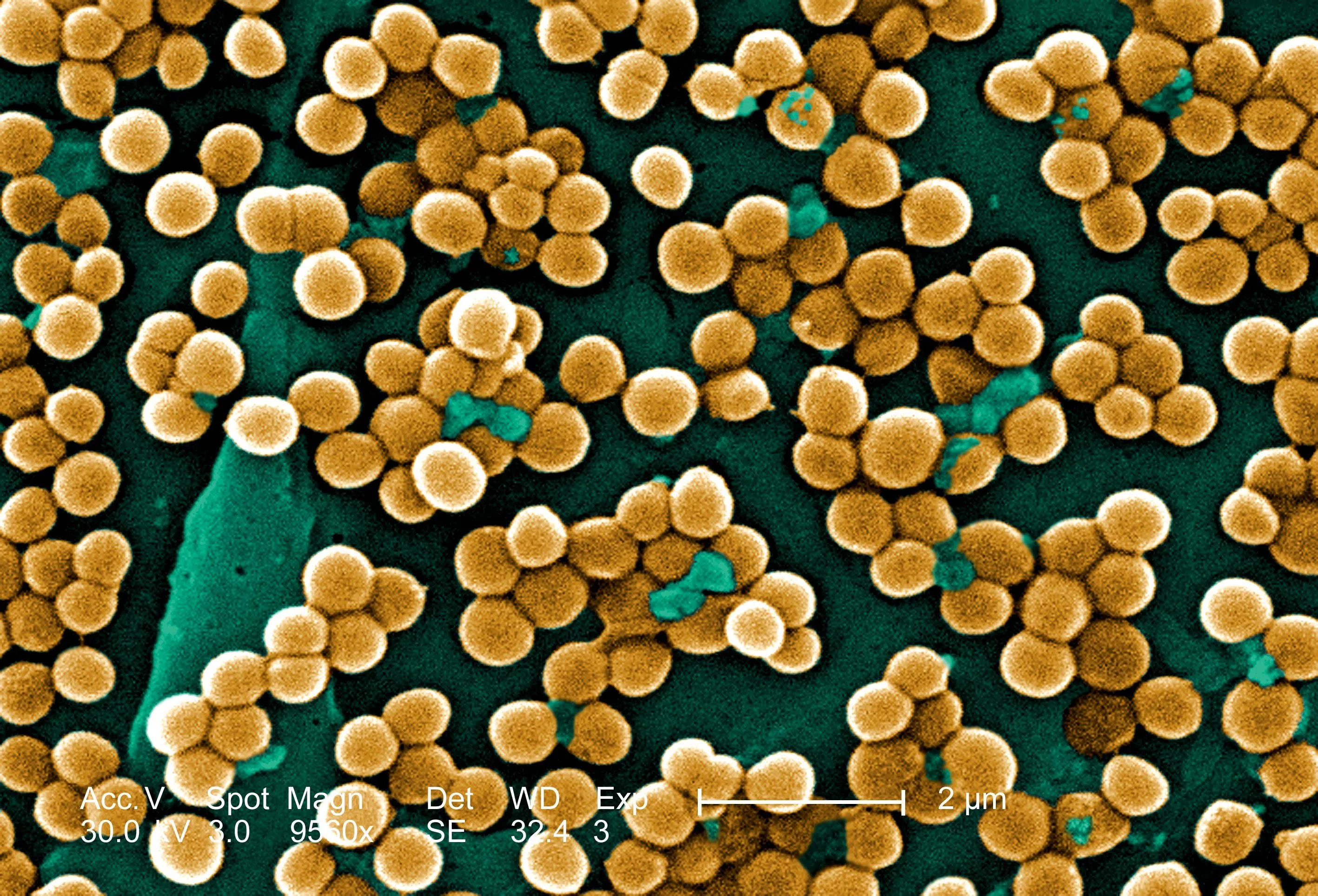

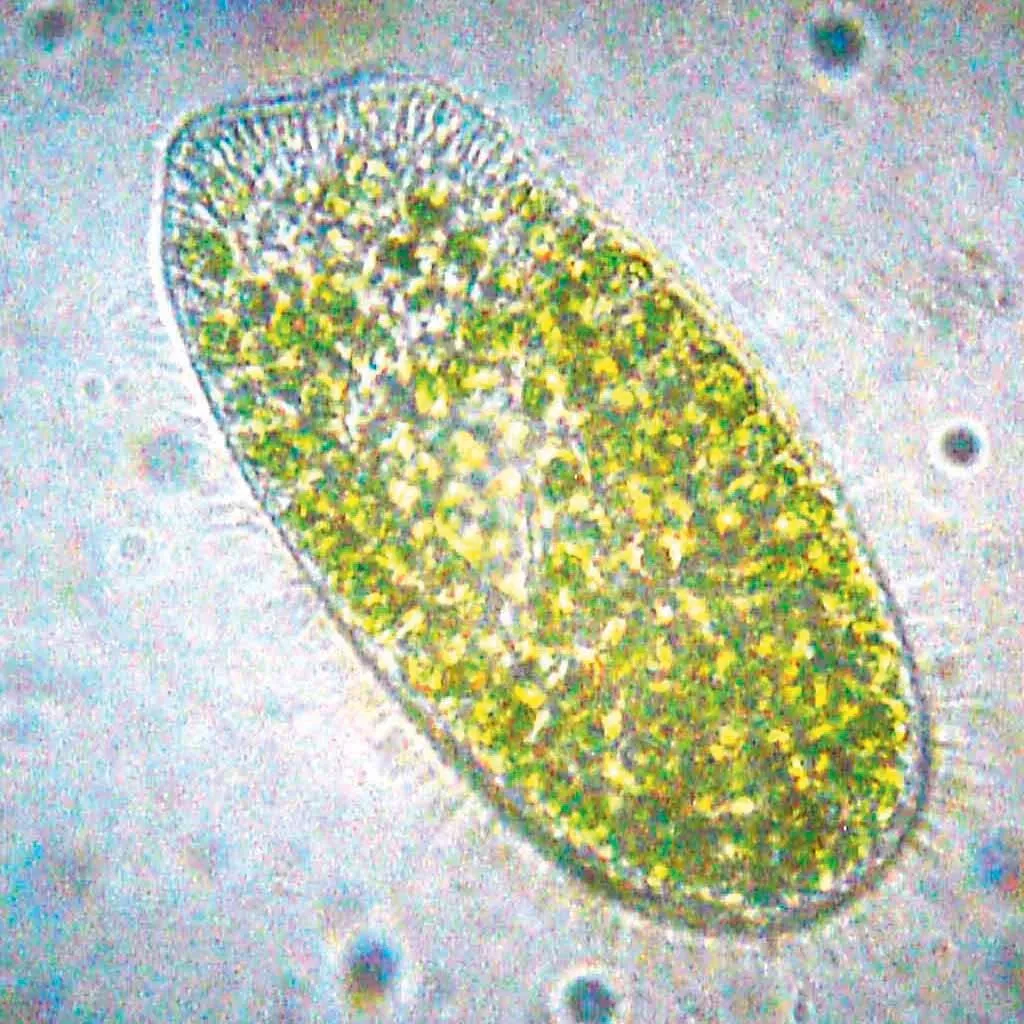
Le streptocoque est une bactérie en forme de boule. Son diamètre peut mesurer jusquʼà 1\text{,}5 \times 10^{-9}~\text{m}.
La paramécie est un petit organisme unicellulaire. Sa longueur peut mesurer jusquʼà 3 \times 10^{-7}~\text{m}.
1. Par quel facteur faut-il multiplier le diamètre dʼun streptocoque pour obtenir la longueur dʼune paramécie ?
La paramécie est un petit organisme unicellulaire. Sa longueur peut mesurer jusquʼà 3 \times 10^{-7}~\text{m}.
1. Par quel facteur faut-il multiplier le diamètre dʼun streptocoque pour obtenir la longueur dʼune paramécie ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce tableau servira aux exercices 50 à 54.
| Objet | Masse (valeurs exemplaires/arrondies/estimées) |
| neutrino | 3\text{,}6 \times 10^{-36} kg |
| électron | 9\text{,}11 \times 10^{-31} kg |
| proton | 1\text{,}67 \times 10^{-27} kg |
| atome d'argent | 1\text{,}79 \times 10^{-25} kg |
| virus de la grippe | 6 \times 10^{-19} kg |
| bactérie E. coli | 1 \times 10^{-15} kg |
| grain de pollen de bouleau | 8 \times 10^{-12} kg |
| ovule humain | 3\text{,}6 \times 10^{-9} kg |
| moustique | 1\text{,}5 \times 10^{-6} kg |
| CD | 1\text{,}5 \times 10^{-2} kg |
| homme adulte | 8\times 10^1 kg |
| baleine bleue (masse record) | 1\text{,}77\times 10^5 kg |
| la grande pyramide de Gizeh | 6\times 10^9 kg |
| tous les poissons de la Terre | 1\text{,}5\times 10^{12} kg |
| l'atmosphère de la Terre | 5\text{,}\times 10^{18} kg |
| la Lune | 7\text{,}35\times 10^{22} kg |
| la Terre | 5\text{,}97\times 10^{24} kg |
| Jupiter | 1\text{,}9\times 10^{27} kg |
| le Soleil | 2\times 10^{30} kg |
| la Voie lactée | 2\times 10^{42} kg |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50Neutrino, Terre et Voie lactée.
1. Par quel facteur faut-il multiplier la masse de la Terre pour obtenir celle du Soleil ?
2. Quel est le pourcentage de la masse de la Voie lactée représenté par la Terre ?
3. Par quel facteur faut-il multiplier la masse dʼun neutrino pour obtenir celle de la Voie lactée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51Planètes.
1. Comparez la masse de Jupiter avec la somme des masses de la Terre et de la Lune.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52Savoir refaireDu neutrino à la baleine bleue.
1. Par quel facteur faut-il multiplier la masse dʼun neutrino pour obtenir celle dʼun proton ?
2. Par quel facteur faut-il multiplier la masse dʼune bactérie E. coli pour obtenir celle dʼun moustique ?
3. Par quel facteur faut-il multiplier la masse dʼun électron pour obtenir celle dʼun grain de pollen de bouleau ?
4. Par quel facteur faut-il multiplier la masse dʼun moustique pour obtenir celle dʼune baleine bleue ?
Ressource affich�ée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53La grande pyramide de Gizeh.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54À vous de jouer !
1. Formulez une question et une réponse à partir du calcul suivant.
2. Posez dʼautres questions en rapport avec lʼordre de grandeur des objets de notre univers et répondez-y.
\begin{aligned}
\frac{5,97 \times 10^{24}}{7,35 \times 10^{22}}=\frac{5,97}{7,35} \times 10^{2} & \approx 0,81224 \times 100 \\
& \approx 81,224
\end{aligned}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55Une famille de jumeaux.
Jeanne et Marcel ont eu des jumeaux en 1900. Leurs deux enfants (1re génération) ont à leur tour eu des jumeaux en 1925 et, par la suite, tous leurs descendants, à chaque génération, ont eu des jumeaux.
1. Une génération représente 25 ans. Combien dʼenfants compte la génération de 1975 ? De 2000 ? De 2025 ? De 2100 ?
2. À partir de quelle date les générations compteront-elles plus de 1 000 personnes ? Plus de 10 000 ? Plus de 100 000 ?
3. Combien de descendants toutes générations confondues Jeanne et Marcel ont-ils en 1975 ? En 2000 ? En 2100 ?
1. Une génération représente 25 ans. Combien dʼenfants compte la génération de 1975 ? De 2000 ? De 2025 ? De 2100 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56Chaîne de mails.
Laure lance une chaîne de mails le jour n° 1 : chaque personne qui la reçoit doit lʼenvoyer à son tour à 3 personnes le lendemain.
1. Combien de personnes reçoivent la chaîne le jour n° 2 ? Et le jour n° 3 ? Le jour n° 10 ?
2. Combien de personnes en tout ont reçu la chaîne les 3 premiers jours ? Les 4 premiers jours ? Les 5 premiers jours ? Au bout de n jours ? (On supposera que Laure envoie la chaîne à trois personnes le premier jour.)
1. Combien de personnes reçoivent la chaîne le jour n° 2 ? Et le jour n° 3 ? Le jour n° 10 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58Population de bactéries.
La masse dʼune population de bactéries est de 1 mg et peut doubler en 30 minutes, si les conditions sont favorables.
1. Dans ce cas, quelle est la masse de la population après :
2. Exprimez tous les résultats en écriture scientifique en utilisant le kilogramme comme unité.
1. Dans ce cas, quelle est la masse de la population après :
- 30 min ?
- 1 heure ?
- 5 heures ?
- une journée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57Terre et lune.

- Terre : 1\text{,}27 \times 10^7 m ;
- Lune : 3\text{,}48 \times 10^6 m.
- Terre : 5\text{,}97 \times 10^{24} kg ;
- Lune : 7\text{,}35 \times 10^{22} kg.
- le diamètre de la Terre et celui de la Lune ;
- la superficie de la Terre et celle de la Lune, sachant que la formule de la superficie dʼune sphère est A = 4\pi r^2 ;
- la masse de la Terre et celle de la Lune.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59Amis de Catherine.
Catherine a 20 amis sur Facebook. Chacun de ses amis a 20 amis que Catherine ne connait pas. Et ainsi de suite.
1. Combien « dʼamis dʼamis dʼamis » a Catherine ?
2. « Catherine a à peu près autant dʼamis au sixième degré quʼil y a de personnes qui vivent en France. » Expliquez le sens de cette phrase. Est-elle vraie ou fausse ?
1. Combien « dʼamis dʼamis dʼamis » a Catherine ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60Nénufar.


1. Dans ce cas, après combien de semaines le lac sera-t-il complètement couvert ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61Nicolas a un coffre-fort.
Le verrou est un code à cinq chiffres.
1. Combien de codes possibles peut-il choisir ?
1. Combien de codes possibles peut-il choisir ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63Puissance.
1. Formulez une règle qui permet de déduire le signe dʼune puissance.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62Cadenas.
Walid a oublié le code de son cadenas. Il se rappelle que le dernier chiffre est un 8 mais il a complètement oublié le reste.
1. Sachant que la combinaison comprend 5 chiffres, combien de combinaisons devra-t-il tester dans le pire des cas ?
2. Quelle probabilité que Walid réussisse à ouvrir le cadenas dès le premier essai ?
1. Sachant que la combinaison comprend 5 chiffres, combien de combinaisons devra-t-il tester dans le pire des cas ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64Poumons.
La surface dʼune alvéole est dʼenviron 0,125 \text{~mm}^2. Chacun de nos poumons contient environ 10^8 alvéoles.
1. Quelle est la surface totale des alvéoles dans les deux poumons ? Exprimez le résultat en \text{m}^2.
1. Quelle est la surface totale des alvéoles dans les deux poumons ? Exprimez le résultat en \text{m}^2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65Un peu dʼarithmétique.
1. Quel est le chiffre des unités de 22\:012^2 ? Justifiez votre réponse.
2. Quel est le chiffre des unités de 22\:013^2 ? Justifiez votre réponse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66Démontrons.
1. Démontrez que tous les entiers pairs sont de la forme 2n avec n un entier relatif.
2. Montrez que le carré dʼun entier pair est un entier pair.
3. p est un entier naturel supérieur ou égal à 1. Montrez quʼun entier pair élevé à la puissance p est un entier pair.
4. Démontrez que tous les entiers impairs sont de la forme 2n + 1 avec n un entier relatif.
5. Montrez que le carré dʼun entier impair est un entier impair.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67Division cellulaire.
Lors du processus de reproduction animale, après fécondation, les cellules de lʼembryon se multiplient par division cellulaire à partir dʼune cellule. Une première division se produit immédiatement après la fécondation, puis les divisions en deux se poursuivent au rythme dʼune toutes les dix heures.
1. Combien lʼembryon compte-t-il de cellules après la première division ?
2. Combien de cellules lʼembryon compte-t-il au bout de 24 heures ? Au bout de 5 jours ? Au bout de deux mois ? À la naissance ?
3. Combien de divisions successives se sont produites entre la fécondation et la naissance ?
1. Combien lʼembryon compte-t-il de cellules après la première division ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68Numéro de téléphone.
En France métropolitaine, depuis le 18 octobre 1996, les numéros de téléphone commencent par 0, suivi dʼun indicatif de région ou de type de téléphone.
1. À votre avis, pourquoi a-t-on ajouté le chiffre 0 et lʼindicatif régional devant les anciens numéros de téléphone ?
2. À quelle région correspond un numéro en 01 ? En 02 ? En 03 ? En 04 ? En 05 ? Combien de combinaisons possibles de numéros de téléphone fixe cela représente-t-il ?
3. Depuis 2005, les numéros commençant par 09 désignent les lignes fixes issues des offres groupées téléphone – internet – télévision. Combien de numéros potentiels de lignes fixes y a-t-il désormais ?
4. À quoi correspond un numéro en 06 ? Combien y a-t-il de numéros de téléphone possibles ?
5. Au 31 mars 2012, dʼaprès lʼAutorité de régulation des communications électroniques et des postes (ARCEP), il y a 69,5 millions dʼutilisateurs de téléphones portables en France métropolitaine et dans les DROM. Quel pourcentage de la population française cela représente-t-il ?
6. Depuis 2010, on peut se voir attribuer un numéro de téléphone portable commençant par 07. Vous en avez peut-être même un ! À votre avis, pourquoi ces numéros ont-ils été créés ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69Céline tire des boules dans une urne.
À chaque tirage, elle remet la boule dans lʼurne avant de tirer la suivante. Il y a dans cette urne 3 boules bleues, 5 boules rouges et 2 boules vertes.
1. Combien de suites de couleurs différentes peut-elle obtenir quand elle tire 10 boules ?
1. Combien de suites de couleurs différentes peut-elle obtenir quand elle tire 10 boules ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70Système solaire.
Voici un tableau récapitulatif des diamètres des planètes du système solaire.
1. Sachant que la distance moyenne Terre–Lune est de 384 400 km, combien de planètes pourrait-on faire rentrer entre la Terre et la Lune si les planètes étaient alignées et se touchaient ?
2. Combien de fois peut-on faire rentrer la Terre dans le Soleil ? Combien de fois peut-on faire rentrer Mercure dans le Soleil ?
| Planète | Diamètre | Volume en m^3 |
| Mercure | 4\text{,}880 \times 10^3~\text{km} | 6\text{,}077 \times 10^{19} |
| Vénus | 1\text{,}21 \times 10^7~\text{m} | 9\text{,}285 \times 10^{20} |
| Terre | 12\:740~\text{km} | 1\text{,}084 \times 10^{21} |
| Jupiter | 142\:984\:000\:000\:000~\text{mm} | 1\text{,}525 \times 10^{24} |
| Saturne | 1\text{,}11464 \times 10^{10}~\text{cm} | 9\text{,}048 \times 10^{23} |
| Uranus | 5\:111\:800\times10^3~\text{cm} | 6\text{,}995 \times 10^{22} |
| Neptune | 49\:532~\text{km} | 6\text{,}358 \times 10^{22} |
| Soleil | 1\:391\:000~\text{km} | 1\text{,}412 \times 10^{27} |
1. Sachant que la distance moyenne Terre–Lune est de 384 400 km, combien de planètes pourrait-on faire rentrer entre la Terre et la Lune si les planètes étaient alignées et se touchaient ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71Tweets.
Vous twittez un scoop et vous informez 30 personnes avec ce tweet. Dans les 8 minutes qui suivent, chacune de ces 30 personnes renvoie ce tweet à 30 autres personnes qui ne lʼont pas reçu et ainsi de suite.
1. Combien de personnes sont au courant une heure après lʼenvoi de votre scoop ?
1. Combien de personnes sont au courant une heure après lʼenvoi de votre scoop ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72Planètes habitables dans lʼunivers.
Les scientifiques estiment quʼil y a :
- entre 200 et 400 milliards dʼétoiles dans une galaxie ;
- entre 100 et 500 milliards de galaxies dans lʼUnivers observable ;
- quʼil pourrait y avoir 40 milliards de planètes habitables dans notre galaxie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Exercice numérique
Pour protéger son vélo, Timéo installe un cadenas à 3 chiffres.
Les chiffres possibles sont 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
1. Combien de codes sont possibles ?
2.
Timéo ne souhaite utiliser que des chiffres pairs. Combien de codes sont alors possibles ?
1. Combien de codes sont possibles ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Exercice numérique
Une résistance électrique possède des anneaux de différentes couleurs ayant chacun une signification.
Pour connaître sa valeur, la couleur du premier anneau donne le chiffre des dizaines, le second donne celui des unités et le dernier le coefficient multiplicateur suivant le tableau suivant.
Pour connaître sa valeur, la couleur du premier anneau donne le chiffre des dizaines, le second donne celui des unités et le dernier le coefficient multiplicateur suivant le tableau suivant.
| Couleur | Anneaux 1 ou 2 | Coefficient multiplicateur |
| Noir | 0 | 1 |
| Marron | 1 | 10 |
| Rouge | 2 | 10^{2} |
| Orange | 3 | 10^{3} |
| Jaune | 4 | 10^{4} |
| Vert | 5 | 10^{5} |
| Bleu | 6 | 10^{6} |
| Violet | 7 | 10^{7} |
| Gris | 8 | 10^{8} |
| Blanc | 9 | 10^{9} |
1.
Calculer la valeur décimale des résistances des composants suivants :


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Tâche complexeProtéger ses données, protéger son identité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Victor et Asma testent un logiciel permettant de trouver des mots de passe. Asma crée un mot de passe et Victor doit essayer de le décoder. Combien de temps, au maximum, faut-il à Victor pour trouver le mot de passe composé par Asma ?
1. Lors de la dernière tentative d'Asma.
2. En général, en posant a le nombre de lettres et b le nombre de chiffres qui composent le message.
1. Lors de la dernière tentative d'Asma.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Le mot de passe.
Les règles du jeu sont simples. Asma compose un mot de passe de 11 caractères avec des lettres et des chiffres. Les lettres peuvent être en majuscule ou en minuscule. Elle dit ensuite à Victor combien de lettres et combien de chiffres elle a choisi, mais pas l'ordre. Victor n'a plus alors qu'à tester toutes les combinaisons possibles avec ces nombres de lettres et de chiffres. Lors de sa dernière tentative, Asma a utilisé 7 lettres et 4 chiffres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Casser un code.
Il existe plusieurs façons de casser un mot de passe, c'est-à-dire de trouver le mot de passe de quelqu'un. La méthode la plus évidente est tout simplement d'essayer toutes les combinaisons possibles jusqu'à trouver le bon mot de passe. C'est d'ailleurs la solution utilisée par la plupart des logiciels. Un ordinateur classique, avec le bon logiciel, peut essayer un milliard de combinaisons par seconde.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
