Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 9
Pas à pas
2. Angles aigus, obtus et droits
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
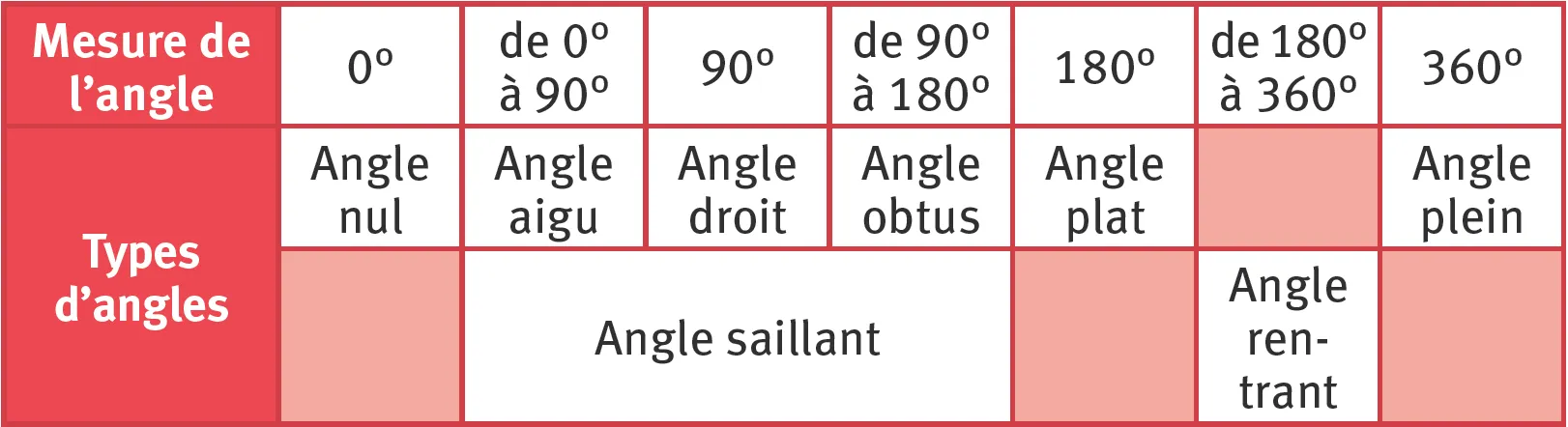
Retenir
- On peut décrire qualitativement un angle en le classant dans de grandes catégories.
- On a quelques angles particuliers.
Le zoom est accessible dans la version Premium. - On peut comparer des angles à l'angle droit.
Le zoom est accessible dans la version Premium. - On peut comparer des angles à l'angle plat.
- On a quelques angles particuliers.
- Pour résumer.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Comparer qualitativement des angles
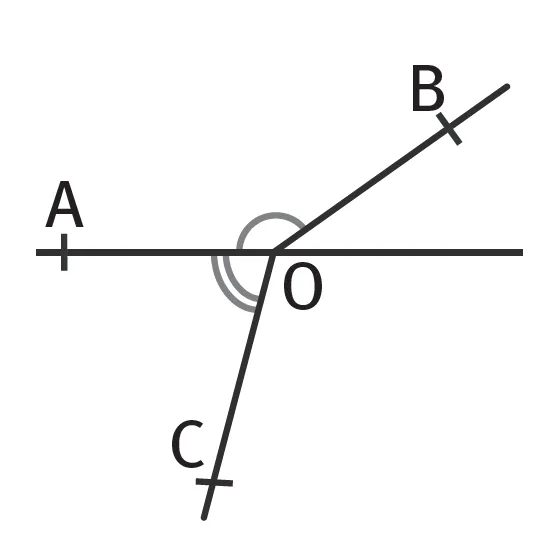
Comparer à l'œil nu les angles \widehat{\text{AOB}} et \widehat{\text{AOC}}.
- À l'œil nu on voit que \widehat{\text{AOC}} est un angle aigu.
- À l'œil nu on voit que \widehat{\text{AOB}} est un angle obtus.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
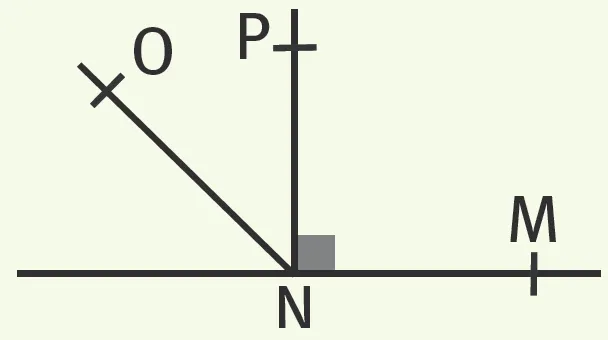
Exercice 5Comparer à l'œil nu les angles suivants
S'il y a un doute, vérifier avec le rapporteur.
1. \widehat{\text{MNO}} et \widehat{\text{MNP}}.
Le zoom est accessible dans la version Premium.
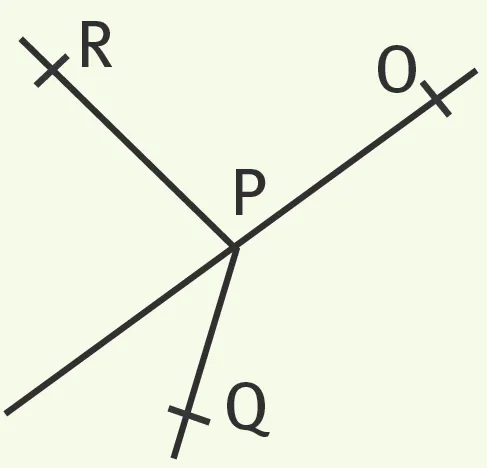
2. \widehat{\text{OPQ}} et \widehat{\text{OPR}}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
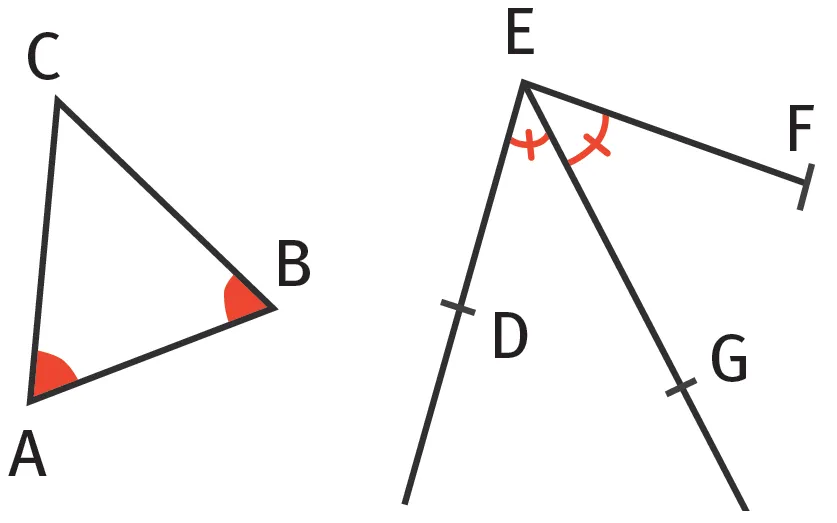
Retenir
- Deux angles de même mesure sont codés de la même façon !
- Ici \widehat{\text{BAC}} = \widehat{\text{CBA}} et \widehat{\text{DEG}} = \widehat{\text{GEF}}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
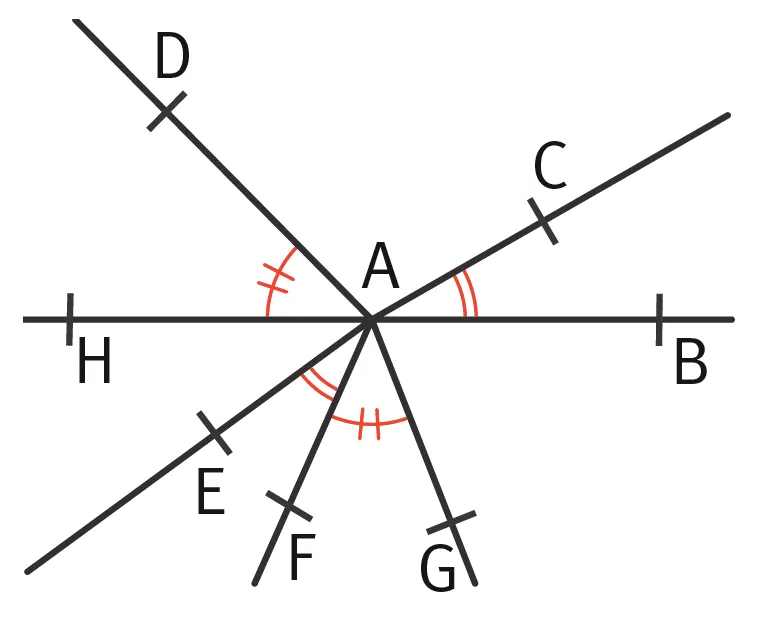
Refaire Repérer des angles de même mesure
Citer les angles égaux.
- On repère les angles codés de la même manière.
- Angles barrés : \widehat{\text{DAH}} = \widehat{\text{FAG}}.
- Angles marqués doublement : \widehat{\text{BAC}} = \widehat{\text{EAF}}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
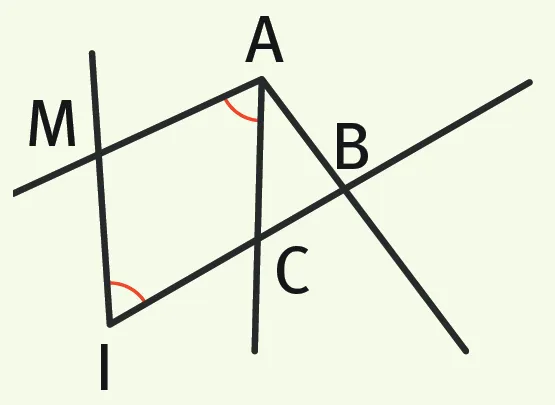
Exercice 6Quels angles sont égaux ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
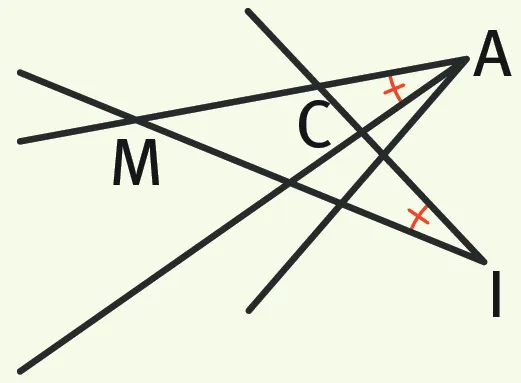
Exercice 7Quels angles sont égaux ?
Le zoom est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah