Mathématiques 6e
Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Mes Pages
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 9
Exercices
Angles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Échauffement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8

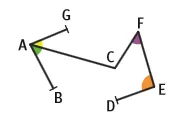
Nommer les angles colorés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Colorier les angles \widehat{\text{BAH}} ; \widehat{\text{AHC}} ; \widehat{\text{DHG}} et \widehat{\text{GFE}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10

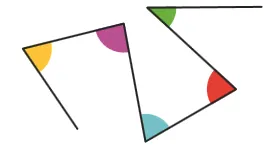
Mesurer avec un rapporteur les angles colorés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11

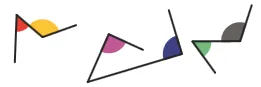
Ranger à l'œil nu les angles colorés dans le tableau suivant.
| Type d'angle | Aigu | Droit | Obtus |
| Angles |
|
|
|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12
Reproduire l'angle suivant sur du papier calque.

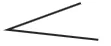
Utiliser ce gabarit pour comparer cet angle aux angles colorés suivants.

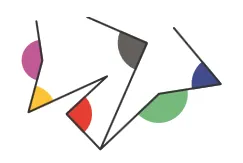


Utiliser ce gabarit pour comparer cet angle aux angles colorés suivants.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13
Construire trois angles de mesures 25^{\circ}, 35^{\circ} et 75^{\circ}.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14
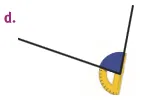
Dans chaque cas, le rapporteur est-il bien placé pour mesurer l'angle coloré ? Justifier vos réponses.

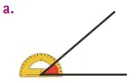

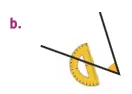

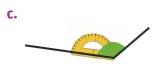









Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15
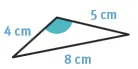
Construire à l'aide d'une règle et d'un compas l'angle coloré suivant.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
Construire un angle \widehat{\text{ABC}} de mesure 35^{\circ} avec AB = 8 cm et CB = 3 cm.
Les dimensions données ici ont-elles une importance pour construire l'angle ?
Les dimensions données ici ont-elles une importance pour construire l'angle ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
Construire un angle \widehat{\text{BIG}} de mesure 67^{\circ}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
Construire un angle \widehat{\text{TAM}} de mesure 142^{\circ}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
En utilisant une équerre, dire si chaque angle coloré est aigu, obtus ou droit.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
Construire la bissectrice de chaque angle coloré.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
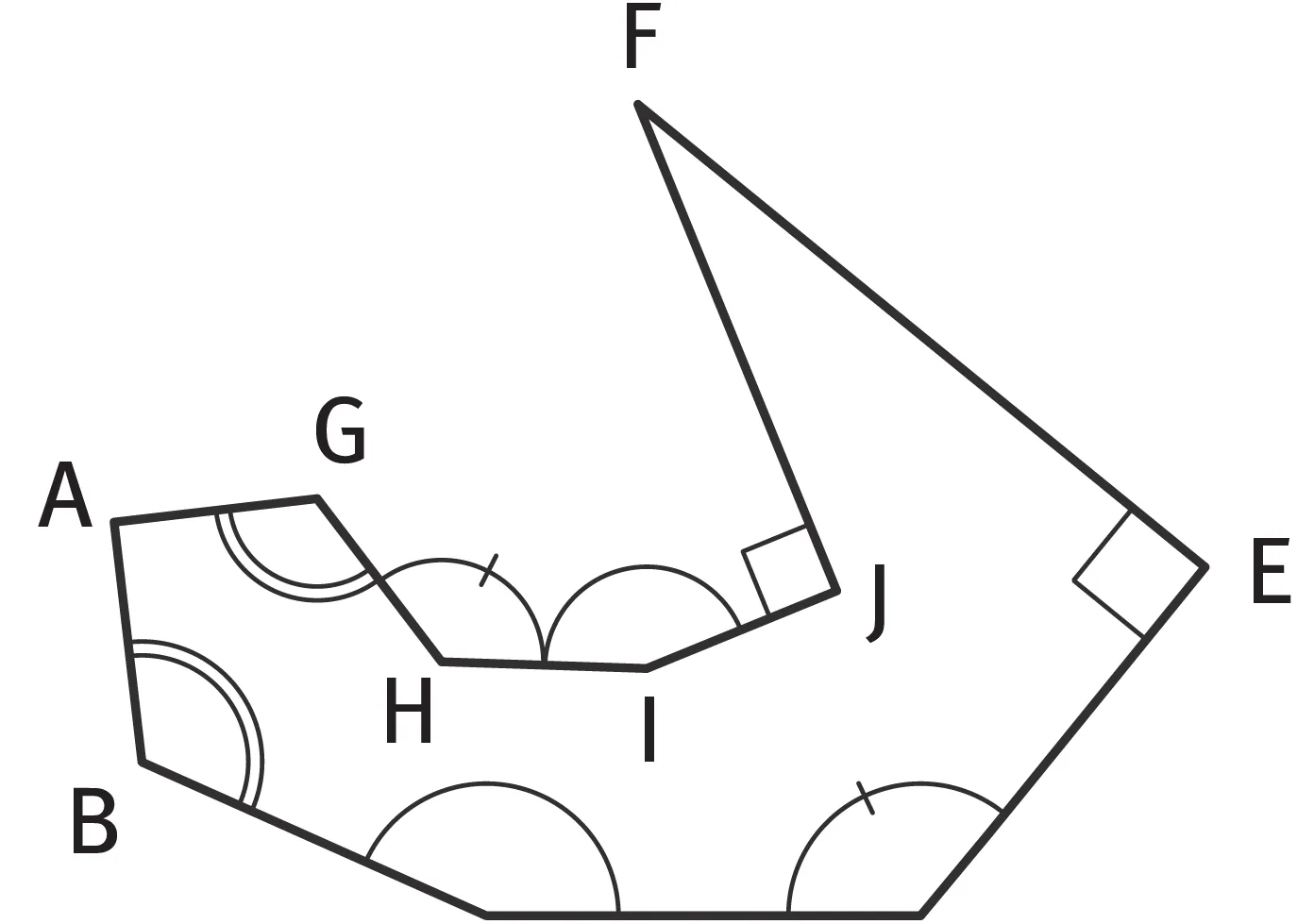
Nommer les angles qui sont égaux entre eux.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Entraînement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
La bissectrice de l'angle \widehat{\text{CRI}} est déjà tracée. Tracer cet angle, sachant qu'il mesure 82°.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Avec un logiciel de géométrie dynamique.
Placer deux points A et B, ainsi que O le milieu de [AB]. Tracer le cercle de centre O et passant par A et B. Placer un point C sur ce cercle et afficher la mesure de l'angle \widehat{\text{BCA}}. Déplacer le point C. Que remarque-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Mesurer les angles \widehat{\text{BCD}} et \widehat{\text{CBA}} puis reproduire la figure en les codant correctement.
![Placeholder pour Schéma géométrique : deux droites parallèles coupées par une sécante. Segments [CD] et [AB] sont traversés par [CB].](https://assets.lls.fr/pages/52666852/c9.24.svg)
![Schéma géométrique : deux droites parallèles coupées par une sécante. Segments [CD] et [AB] sont traversés par [CB].](https://assets.lls.fr/pages/52666852/c9.24.webp)
Comment semblent être les droites (AB) et (CD) ?
![Placeholder pour Schéma géométrique : deux droites parallèles coupées par une sécante. Segments [CD] et [AB] sont traversés par [CB].](https://assets.lls.fr/pages/52666852/c9.24.svg)
![Schéma géométrique : deux droites parallèles coupées par une sécante. Segments [CD] et [AB] sont traversés par [CB].](https://assets.lls.fr/pages/52666852/c9.24.webp)
Comment semblent être les droites (AB) et (CD) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Étymologie.
1. Rechercher l'origine du mot « polygone ».
2. D'autres mots français ont-ils la même origine ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Construire un triangle ABC tel que \widehat{\text{BAC}} = 60^{\circ} et \widehat{\text{CBA}} = 45^{\circ}.
Combien mesure l'angle \widehat{\text{ACB}} ?
Combien mesure l'angle \widehat{\text{ACB}} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Construire un triangle quelconque. Construire les bissectrices de ses angles.
Que remarque-t-on ?
Que remarque-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
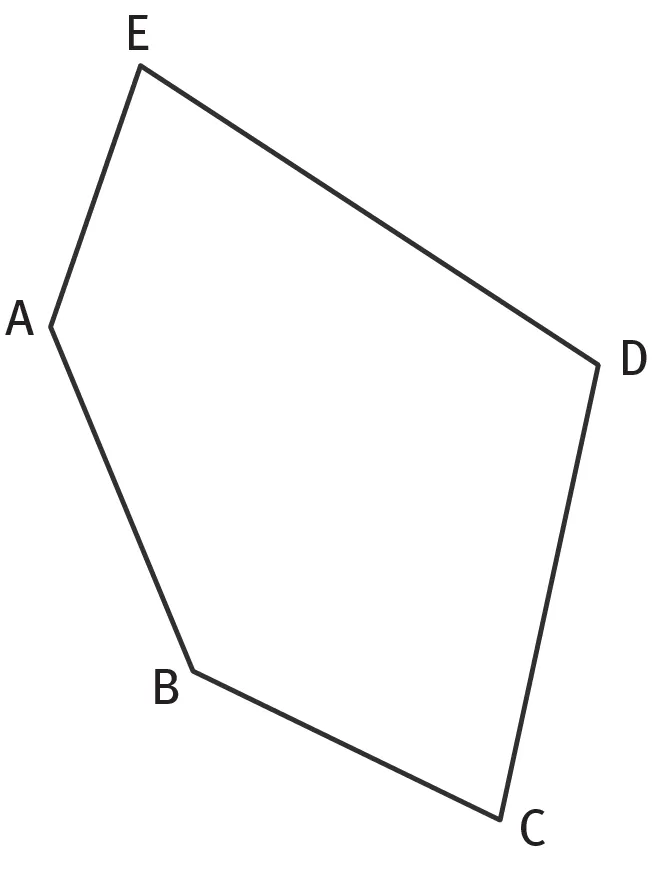
Mesurer les angles \widehat{\text{BAE}} ; \widehat{\text{DCB}} et \widehat{\text{AED}}.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
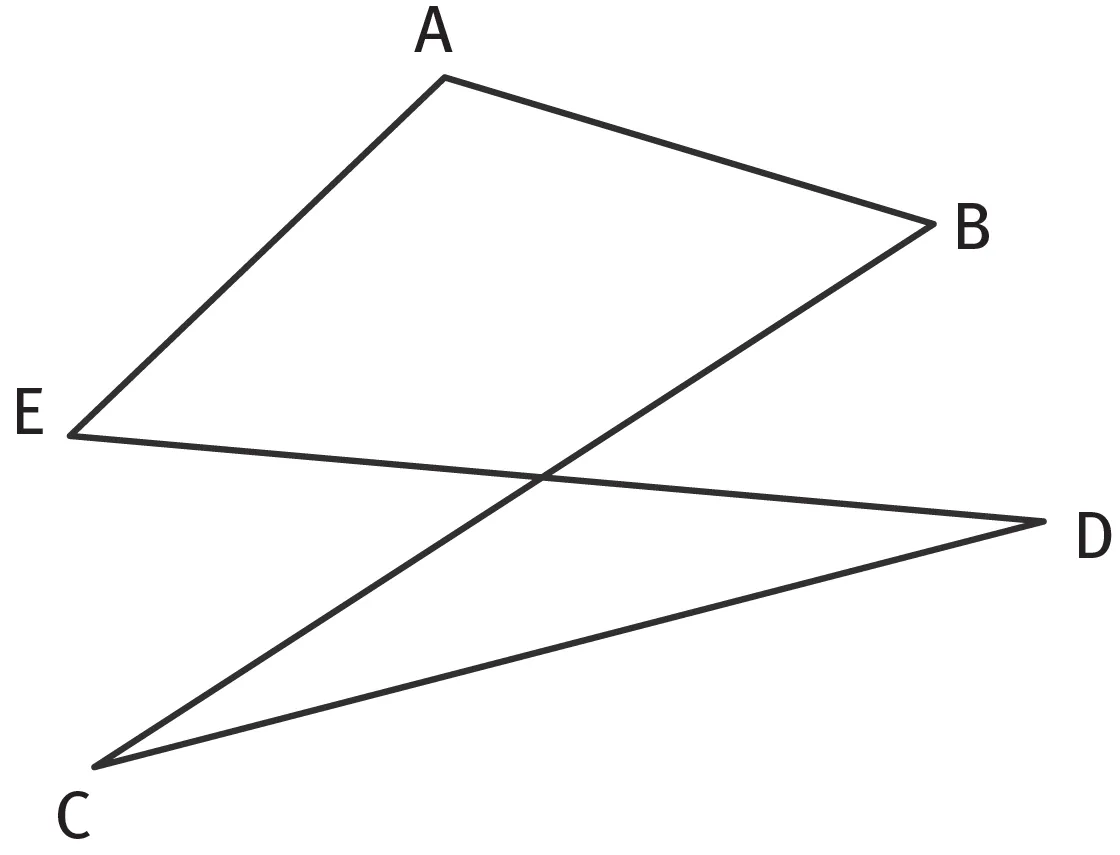
29
Mesurer les angles \widehat{\text{EAB}} ; \widehat{\text{BCD}} et \widehat{\text{DEA}}.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
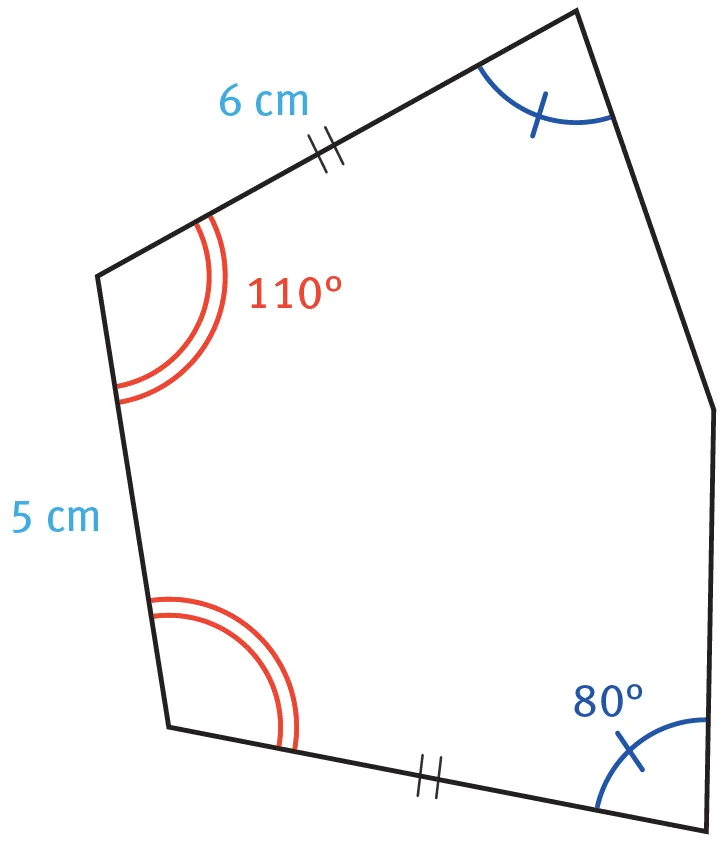
30
Reproduire la figure suivante.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31 Lancer de poids.
Lors d'une compétition de lancer de poids, le lanceur doit envoyer le poids dans un secteur angulaire mesurant environ 35^{\circ}, centré en l'endroit où il lance le poids.




Représenter schématiquement un terrain de lancer de poids.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
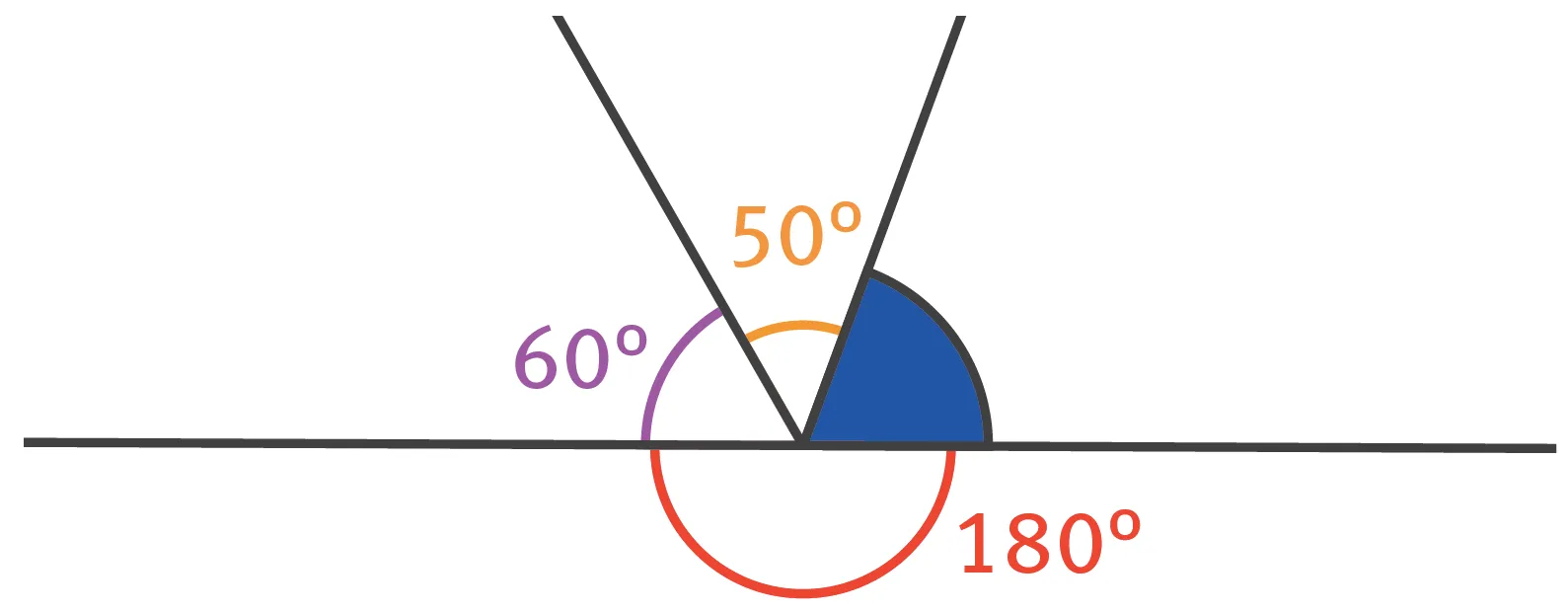
32
Donner la mesure de l'angle coloré en bleu.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33Construire la figure suivante.
1. Tracer un cercle de centre O et de rayon quelconque.
2. Placer deux points M et N sur ce cercle.
3. Tracer la droite qui coupe \widehat{\text{MON}} en deux angles égaux.
4. Quelle propriété semble vérifier cette droite par rapport au segment [MN] ?
2. Placer deux points M et N sur ce cercle.
3. Tracer la droite qui coupe \widehat{\text{MON}} en deux angles égaux.
Cliquez pour accéder à une zone de dessin
4. Quelle propriété semble vérifier cette droite par rapport au segment [MN] ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
Bérénice partage un gâteau circulaire de 18 cm de rayon pour son anniversaire.




Pour s'amuser, elle prend son rapporteur en chocolat et fait des parts mesurant 23^{\circ}. Combien de personnes pourra-t-elle servir au maximum ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
Placer trois points \mathrm{B}, \mathrm{I} et \mathrm{M} tels que \widehat{\text{BIM}} = 135°.
1. Placer un point \mathrm{T} tel que \mathrm{[IT)} soit la bissectrice de l'angle \widehat{\mathrm{BIM}}.
2. Placer un point \mathrm{H} tel que \mathrm{[IH)} soit la bissectrice de l'angle \widehat{\mathrm{TIM}}.
3. Quelle est la mesure de l'angle \widehat{\text{HIM}} ?
1. Placer un point \mathrm{T} tel que \mathrm{[IT)} soit la bissectrice de l'angle \widehat{\mathrm{BIM}}.
2. Placer un point \mathrm{H} tel que \mathrm{[IH)} soit la bissectrice de l'angle \widehat{\mathrm{TIM}}.
3. Quelle est la mesure de l'angle \widehat{\text{HIM}} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
Sur un terrain de football, les cages mesurent 7,30 m de large. Le point de penalty se situe à 11 m des cages, « en face » de leur milieu.
Faire un schéma des cages et du point de penalty afin de mesurer l'angle sous lequel un footballeur voit les cages quand il tire un penalty.


Faire un schéma des cages et du point de penalty afin de mesurer l'angle sous lequel un footballeur voit les cages quand il tire un penalty.


Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37
Manon joue à colin-maillard avec des amis.
Rémi se place devant elle et la fait tourner sur elle-même, en lui faisant faire un nombre impair de demi-tours. Rémi se retrouvera-t-il devant ou derrière elle ? Pourquoi ?
Rémi se place devant elle et la fait tourner sur elle-même, en lui faisant faire un nombre impair de demi-tours. Rémi se retrouvera-t-il devant ou derrière elle ? Pourquoi ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
Nicolas a recopié une figure pour Marie, mais il a oublié de la coder.
Restituer ce codage en utilisant la règle graduée et le rapporteur de manière à ce que Marie puisse facilement la reproduire.
Restituer ce codage en utilisant la règle graduée et le rapporteur de manière à ce que Marie puisse facilement la reproduire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
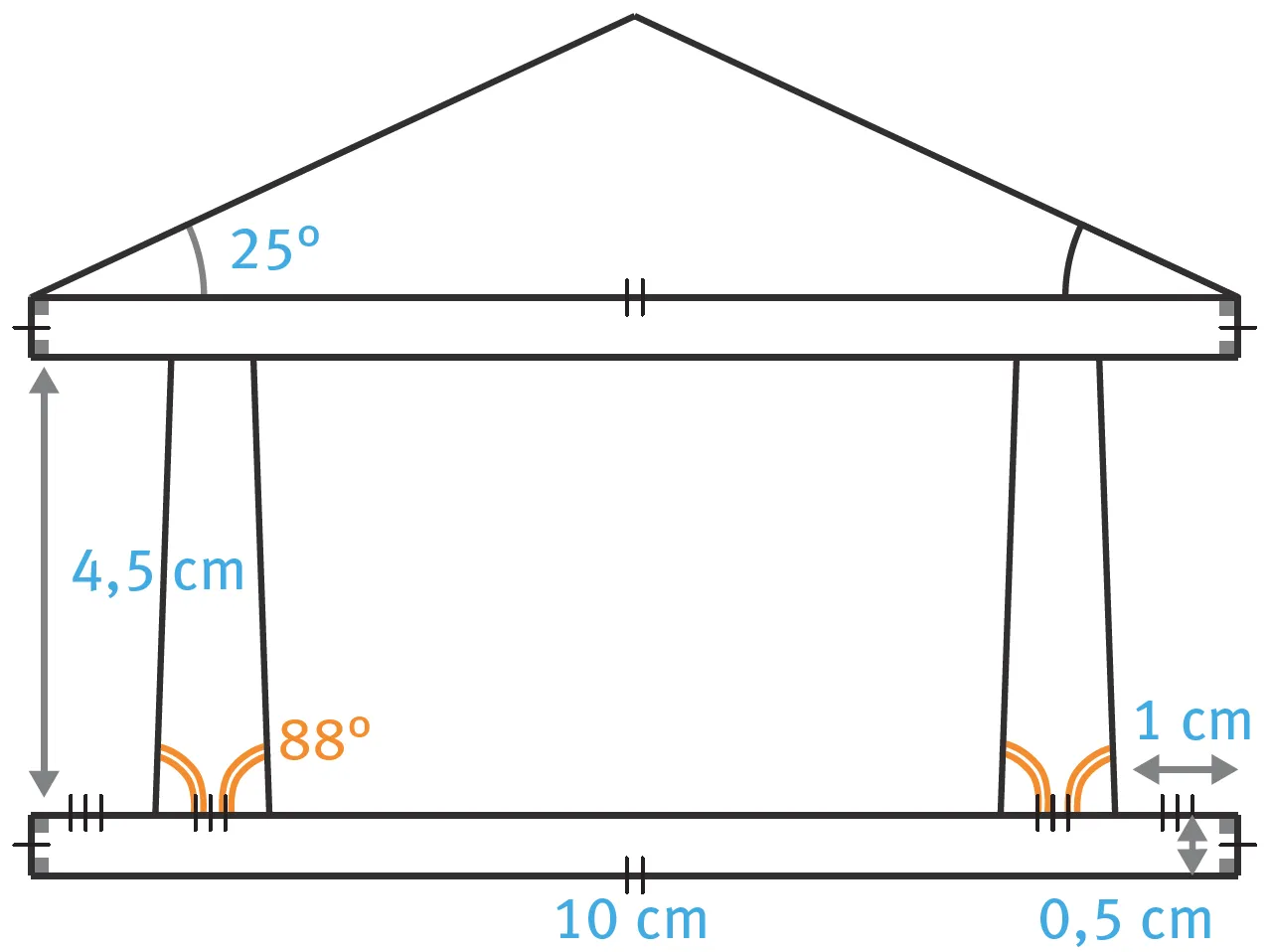
Reproduire ce plan de façade de temple grec.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
Expliquer pourquoi chaque affirmation est fausse.
1. 115^{\circ} est un angle aigu.
2. Si on additionne les mesures de deux angles aigus, on obtient forcément la mesure d'un angle obtus.
3. Si on prolonge les côtés d'un angle, sa mesure augmente.
1. 115^{\circ} est un angle aigu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compétition
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
Camille observe un bateau de 10 m de large, placé 10 m devant elle.




1. Combien mesure l'angle sous lequel Camille voit le bateau ?
2. Ce dernier s'éloigne et se trouve maintenant à 50 m de Camille. A-t-elle l'impression que le bateau est plus grand ou plus petit ?
3. Comment interpréter ce phénomène avec des angles ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
Construire un triangle \mathrm{YOU} tel que \widehat{\text{YOU}} = 65^{\circ}, \widehat{\text{OYU}} = 28^{\circ} et \mathrm{YO = 4~cm.}
1. Y a-t-il plusieurs triangles constructibles de la sorte ?
2. Tous les triangles constructibles ainsi ont-ils l'air d'être superposables ?
1. Y a-t-il plusieurs triangles constructibles de la sorte ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43Qui a raison ?
Pierre utilise sa règle et dit que les points B, A et F sont alignés. Cécile regarde le dessin, réfléchit quelques secondes et lui dit que ce n'est pas possible.

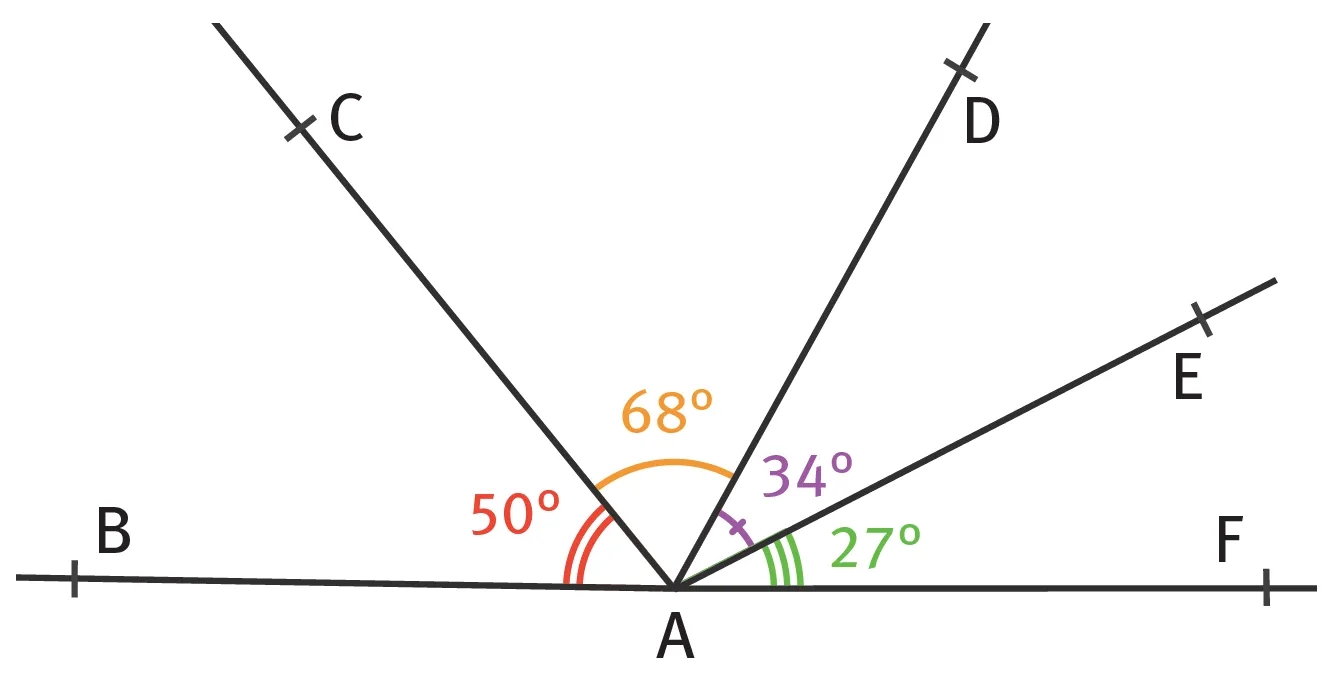 Qui a raison ? Pourquoi ?
Qui a raison ? Pourquoi ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
Le papa de Matthieu veut construire un toit incliné de 50^{\circ} par rapport au sol.
Pour le soutenir, il veut poser un pilier vertical à 50 cm de l'angle formé par le sol et le toit et un second pilier placé à 3 m de cet angle. Quelle sera la hauteur de ces piliers ? On pourra réaliser un schéma pour s'aider.


Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
Dans un diagramme circulaire ou semi-circulaire, les angles des portions sont proportionnels aux quantités représentées par ces portions.
Compléter le tableau suivant et tracer un diagramme circulaire représentant ces données.
Compléter le tableau suivant et tracer un diagramme circulaire représentant ces données.
Proportions de bacheliers dans la population selon le type de baccalauréat.
| Type de baccalauréat | Proportion de la population française, en 2009 | Angle dans un diagramme semi-circulaire | Angle dans un diagramme circulaire |
| Baccalauréat général | 35 % |
|
|
| Baccalauréat technologique | 16 % |
|
|
| Baccalauréat professionnel | 14 % |
|
|
| Sans baccalauréat | 35 % |
|
|
| Total | 100 % |
|
|
www.education.gouv.fr
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46Triangulation.
Nicolas, Ruben et Adrien sont des bricoleurs ingénieux et ont fabriqué un dispositif de triangulation. Il permet à Nicolas (point N) et Adrien (point A) de localiser précisément Ruben (point R), qui s'est perdu. Le système les informe que l'angle \widehat{\text{ANR}} mesure 66^{\circ} et que l'angle \widehat{\text{RAN}} mesure 86^{\circ}.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47Diamètre angulaire de la Lune.
Lors d'un soir où la Lune est visible, tendre une règle graduée à bout de bras et mesurer le diamètre de la Lune.




Reproduire le schéma suivant où 1 cm représente 10 cm en réalité. En déduire une mesure de l'angle coloré.

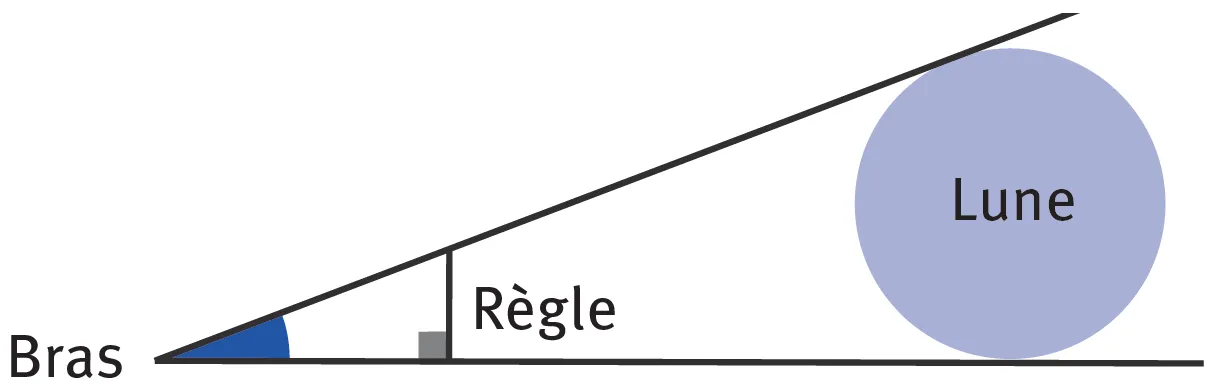


Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48Programme de construction.
1. Tracer un cercle de diamètre 5 cm et de centre I.
2. Placer deux points G et Z sur le cercle tels que la mesure de l'angle \widehat{\text{ZIG}} soit 140^{\circ}.
3. Tracer en rouge la droite perpendiculaire au côté [IZ] et passant par Z.
4. Tracer la droite perpendiculaire au côté [IG] et passant par G. Elle coupera la droite rouge au point A.
5. Tracer la droite qui coupe l'angle \widehat{\text{ZAG}} en deux angles égaux. Que remarque-t-on ?
6. Placer sur le côté [AZ), un point T tel que AT = 10 cm.
7. Tracer [TI) puis tracer le côté manquant de l'angle \widehat{\text{ATX}} afin que [TI) coupe cet angle en deux angles égaux.
8. Le côté tracé coupera la droite (AG) au point C. Que remarque-t-on ?
2. Placer deux points G et Z sur le cercle tels que la mesure de l'angle \widehat{\text{ZIG}} soit 140^{\circ}.
3. Tracer en rouge la droite perpendiculaire au côté [IZ] et passant par Z.
4. Tracer la droite perpendiculaire au côté [IG] et passant par G. Elle coupera la droite rouge au point A.
5. Tracer la droite qui coupe l'angle \widehat{\text{ZAG}} en deux angles égaux. Que remarque-t-on ?
6. Placer sur le côté [AZ), un point T tel que AT = 10 cm.
7. Tracer [TI) puis tracer le côté manquant de l'angle \widehat{\text{ATX}} afin que [TI) coupe cet angle en deux angles égaux.
8. Le côté tracé coupera la droite (AG) au point C. Que remarque-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Socle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCM
1. L'angle semble être :

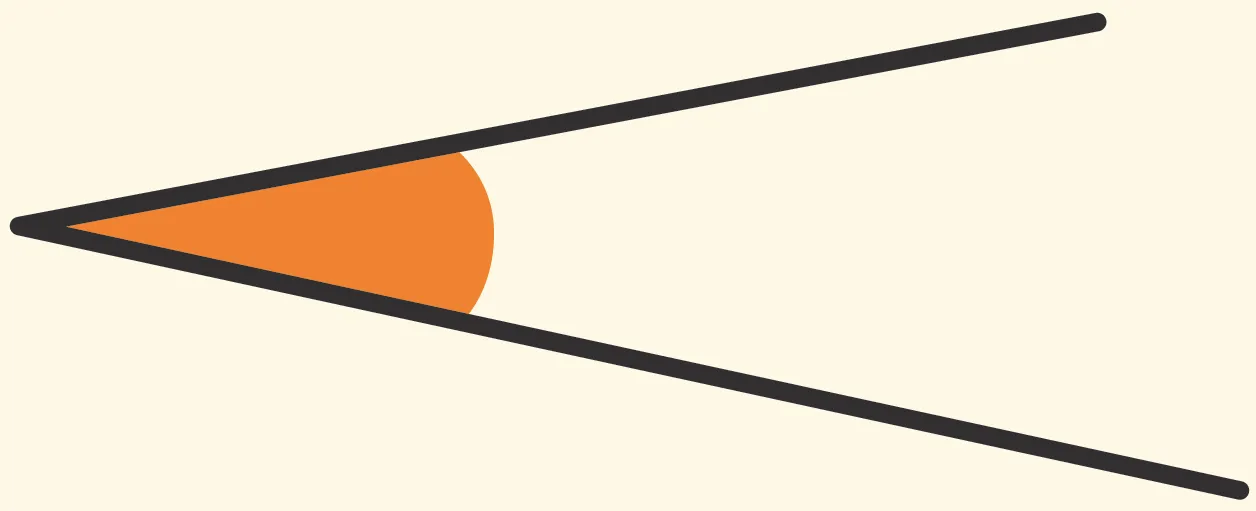
2. L'angle est :


3. Cet angle se note :

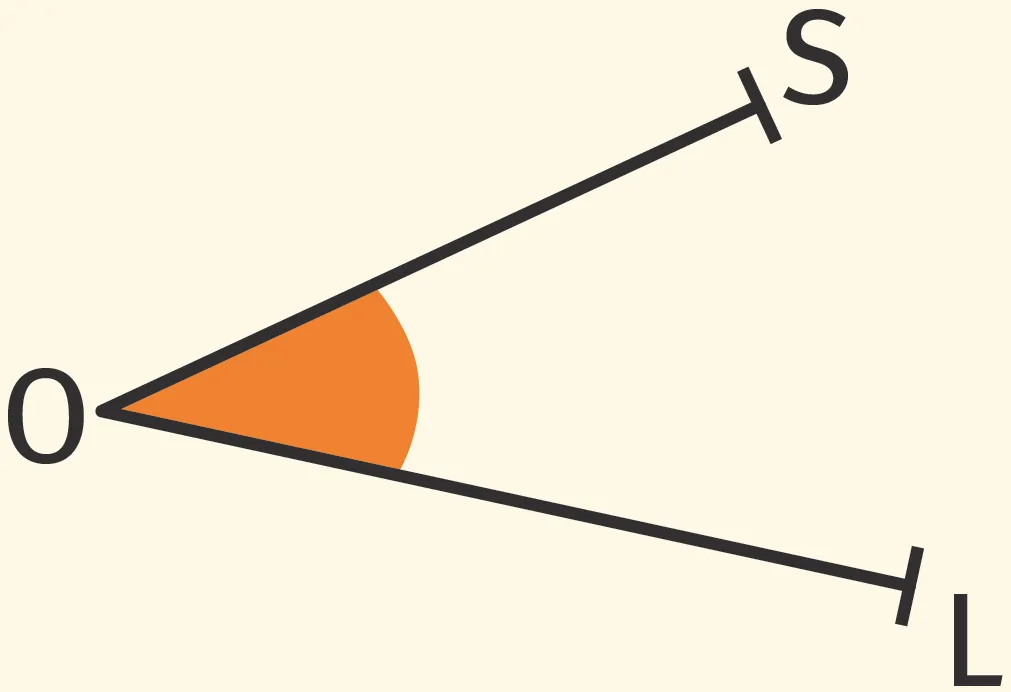
4. Cet angle se note :

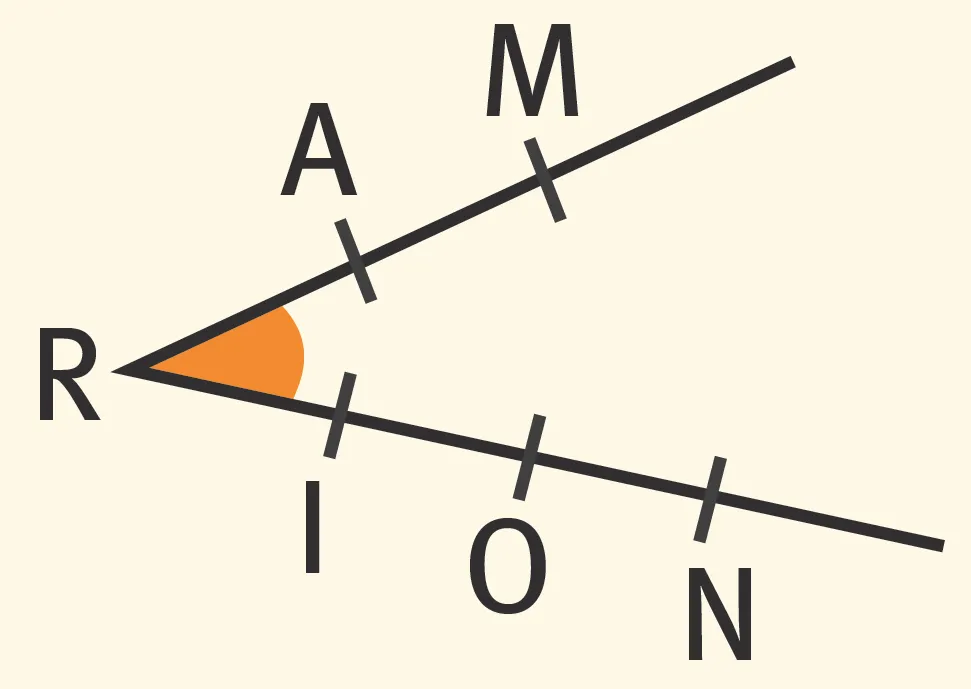
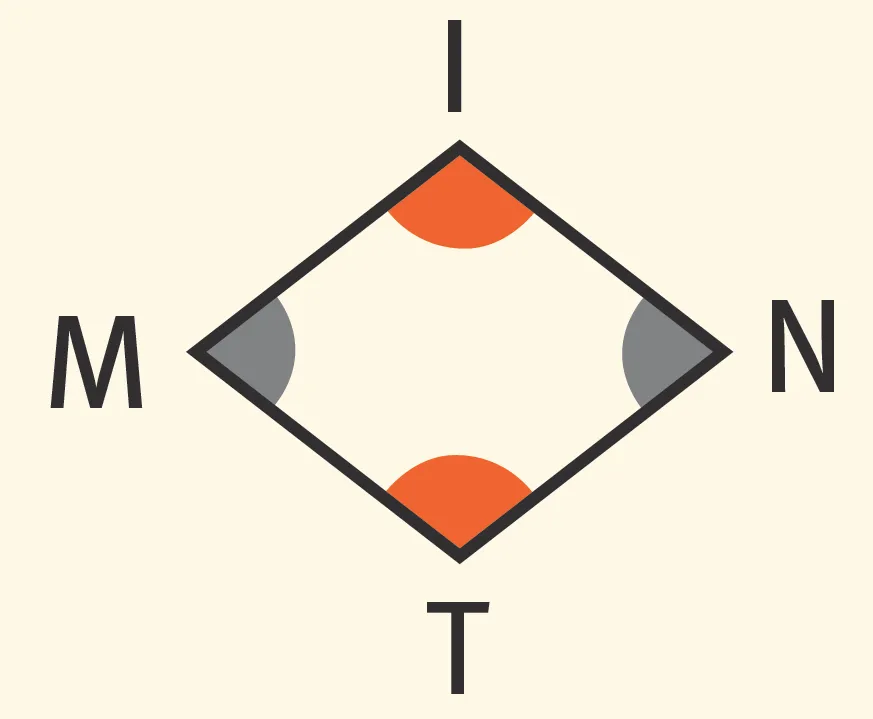
5. Sur cette figure, on a :

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Tâche complexe
Plus un conducteur roule vite, moins il voit de choses autour de lui. Dans une situation donnée, peut-on déterminer quels objets un conducteur aura-t-il une chance d'apercevoir ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Autour des maths
Comment peut-on mesurer la distance d'un objet lointain auquel on ne peut accéder, comme une étoile ? En mesurant des angles : c'est la technique de la parallaxe !
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
