Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 11
Pas à pas
2. Propriétés des quadrilatères usuels
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
Décalquer les figures suivantes et les recopier sur le cahier.
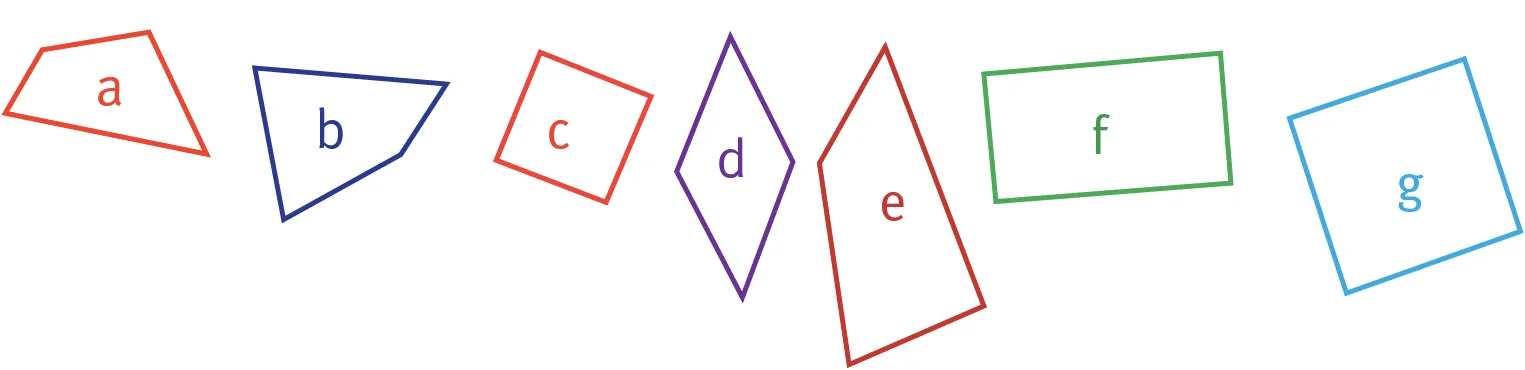a. Coder chaque figure en utilisant les instruments de mesure (règle graduée et équerre).
b. Repérer à l'œil nu les axes de symétrie et les tracer pour chaque figure.
c. Regrouper ces figures dans plusieurs catégories, en fonction des observations précédentes. Des figures pourront éventuellement appartenir à plusieurs catégories.
d. Expliquer le choix des catégories. Les élèves de la classe ont-ils tous choisi les mêmes catégories ?
Le zoom est accessible dans la version Premium.
b. Repérer à l'œil nu les axes de symétrie et les tracer pour chaque figure.
c. Regrouper ces figures dans plusieurs catégories, en fonction des observations précédentes. Des figures pourront éventuellement appartenir à plusieurs catégories.
d. Expliquer le choix des catégories. Les élèves de la classe ont-ils tous choisi les mêmes catégories ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
Définition : Un quadrilatère est une figure ayant quatre côtés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Losange
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
a. Construire un triangle ABC, isocèle en A, avec AB = 5 cm et BC = 3 cm.
b. Construire le symétrique de A par rapport à (BC).
c. Repérer à l'œil nu les axes de symétrie. Lesquels sont-ils ?
d. Vérifier par pliage que les droites repérées sont bien des axes de symétrie.
b. Construire le symétrique de A par rapport à (BC).
c. Repérer à l'œil nu les axes de symétrie. Lesquels sont-ils ?
d. Vérifier par pliage que les droites repérées sont bien des axes de symétrie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
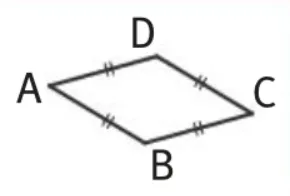
Définition : Un losange ABCD est un quadrilatère dont les quatre côtés sont égaux : AB = BC = CD = DA.
Le zoom est accessible dans la version Premium.
Crédits :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Remarque :
On peut voir plusieurs triangles isocèles dans un losange :
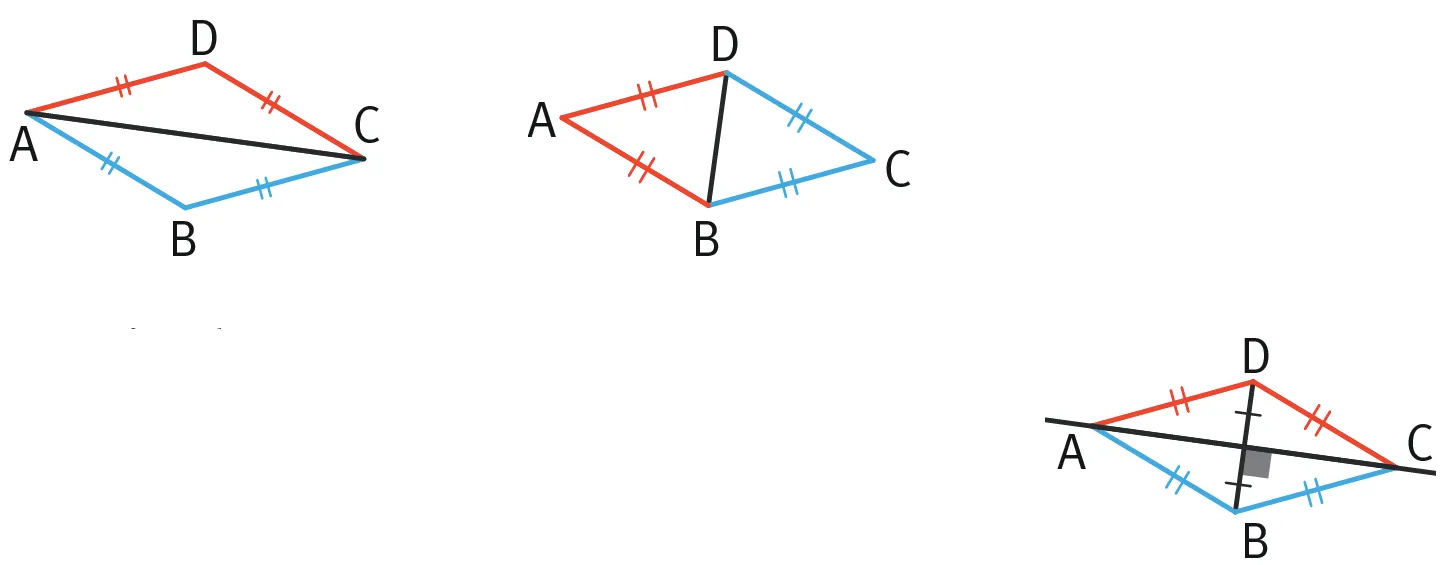
On peut voir plusieurs triangles isocèles dans un losange :
- Ces triangles ont un axe de symétrie en commun : la droite (AC).
- Grâce aux propriétés de la symétrie axiale, on sait que (AC) est la médiatrice de [BD]
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
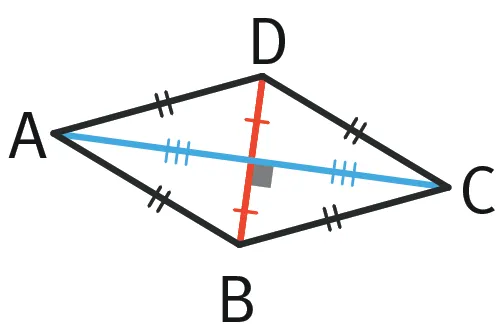
- Un losange ABCD possède deux diagonales : ce sont les segments [AC] et [BD].
- Les diagonales d'un losange se coupent en leur milieu et sont perpendiculaires.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
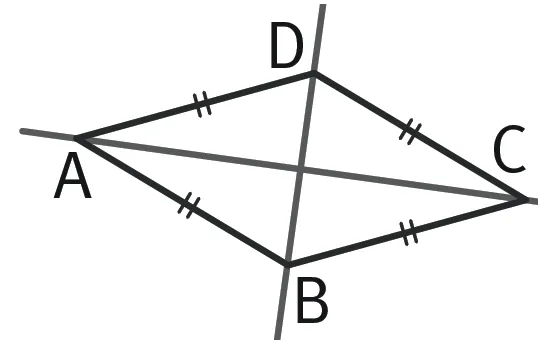
Un losange ABCD possède deux axes de symétrie : les droites (AC) et (BD).
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Remarque :
Dans un losange, après avoir tracé les diagonales, on peut voir quatre triangles rectangles. Ils ont les mêmes dimensions !
Dans un losange, après avoir tracé les diagonales, on peut voir quatre triangles rectangles. Ils ont les mêmes dimensions !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Remarque :
Un losange peut parfois posséder plus de deux axes de symétrie, c'est alors un carré avec quatre axes de symétrie, mais jamais moins !
Un losange peut parfois posséder plus de deux axes de symétrie, c'est alors un carré avec quatre axes de symétrie, mais jamais moins !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Étudier les angles d'un losange
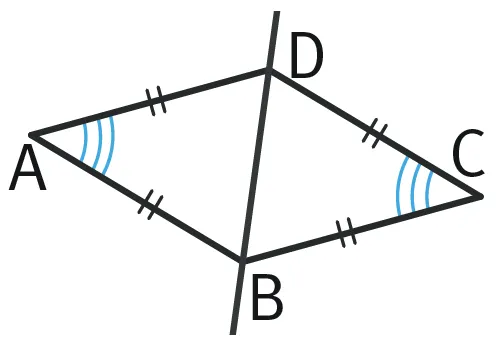
- Montrer que les angles et sont égaux.
- On sait que (BD) est un axe de symétrie : C est le symétrique de A par rapport à (BD).
- B et D sont situés sur l'axe de symétrie : B est le symétrique de B, D est le symétrique de D.
- Donc le symétrique de l'angle est l'angle .
- Or la symétrie conserve les angles.
- Donc les angles et sont égaux.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5 Angles
Le zoom est accessible dans la version Premium.
Montrer que .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
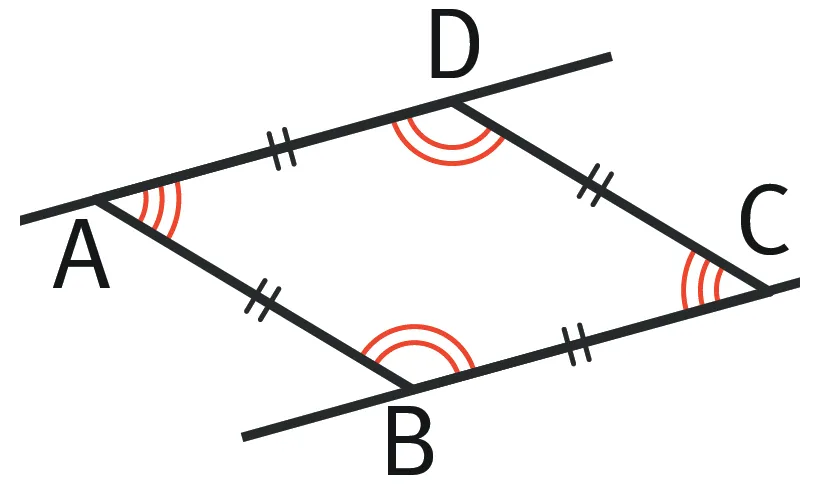
- Dans le losange ABCD, on a et .
- Dans un losange, les côtés opposés sont parallèles.
- (AD) // (BC) et (AB) // (DC).
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BRectangle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
a. Construire un triangle ABC, rectangle en A, tel que AB = 4 cm et AC = 3 cm.
b. Construire ensuite le triangle BCD, rectangle en D, tel que BD = 3 cm et CD = 4 cm.
c. Quelle figure obtient-on ?
d. Repérer à l'œil nu les axes de symétrie, combien sont-ils ?
e. Vérifier par pliage ou à l'aide du papier calque que les droites repérées sont bien des axes de symétrie.
f. Mesurer les angles et .
b. Construire ensuite le triangle BCD, rectangle en D, tel que BD = 3 cm et CD = 4 cm.
c. Quelle figure obtient-on ?
d. Repérer à l'œil nu les axes de symétrie, combien sont-ils ?
e. Vérifier par pliage ou à l'aide du papier calque que les droites repérées sont bien des axes de symétrie.
f. Mesurer les angles et .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
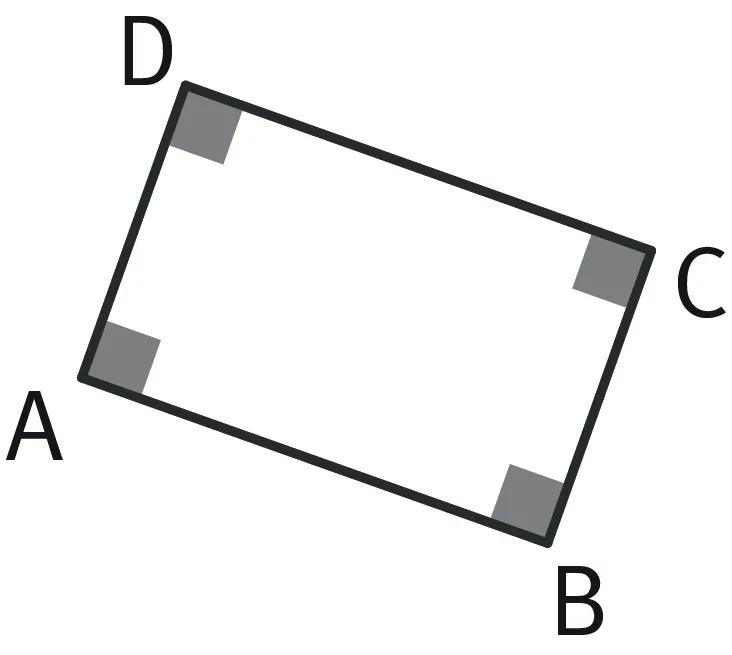
Définition : Un rectangle est un quadrilatère dont les quatre angles sont des angles droits.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple : Le rectangle ABCD.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Établir le parallélisme des côtés d'un rectangle
- Montrer que les droites (AD) et (BC) sont parallèles.
- La droite (AD) est perpendiculaire à la droite (DC) et la droite (BC) est perpendiculaire à la droite (DC).
- Or deux droites perpendiculaires à une même troisième droite sont parallèles.
- Ainsi (AD) est parallèle à (BC) : (AD) // (BC).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6 Parallèles
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
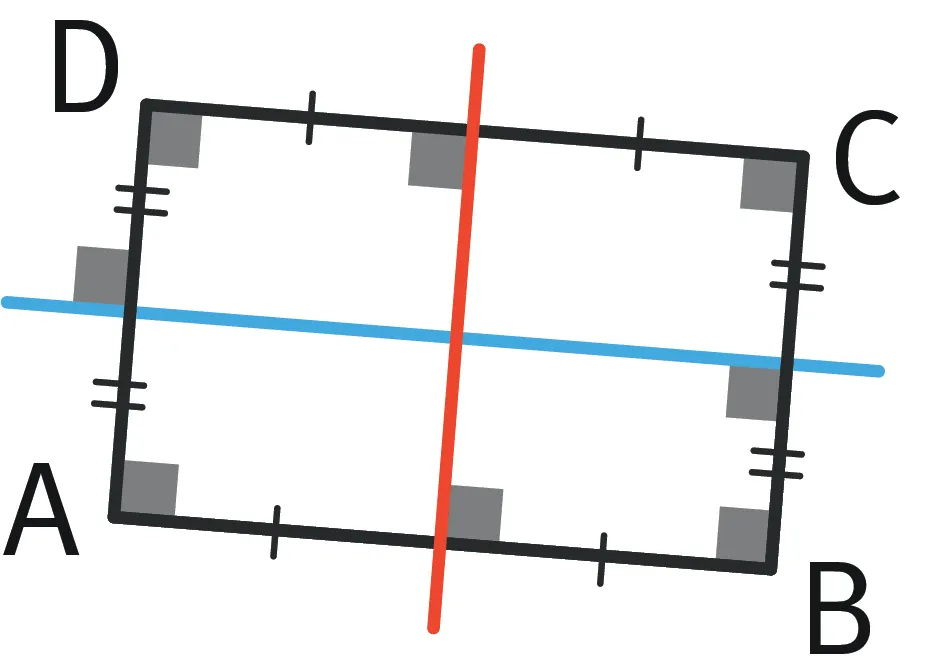
- Les côtés opposés d'un rectangle sont parallèles.
- Un rectangle possède deux axes de symétrie : ce sont les médiatrices de ses côtés.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Remarque :
Un rectangle peut parfois posséder plus d'axes de symétrie, c'est alors un carré avec quatre axes de symétrie, mais jamais moins.
Exemple : Les axes de symétrie du rectangle ABCD sont les droites rouge et bleue.
Un rectangle peut parfois posséder plus d'axes de symétrie, c'est alors un carré avec quatre axes de symétrie, mais jamais moins.
Exemple : Les axes de symétrie du rectangle ABCD sont les droites rouge et bleue.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
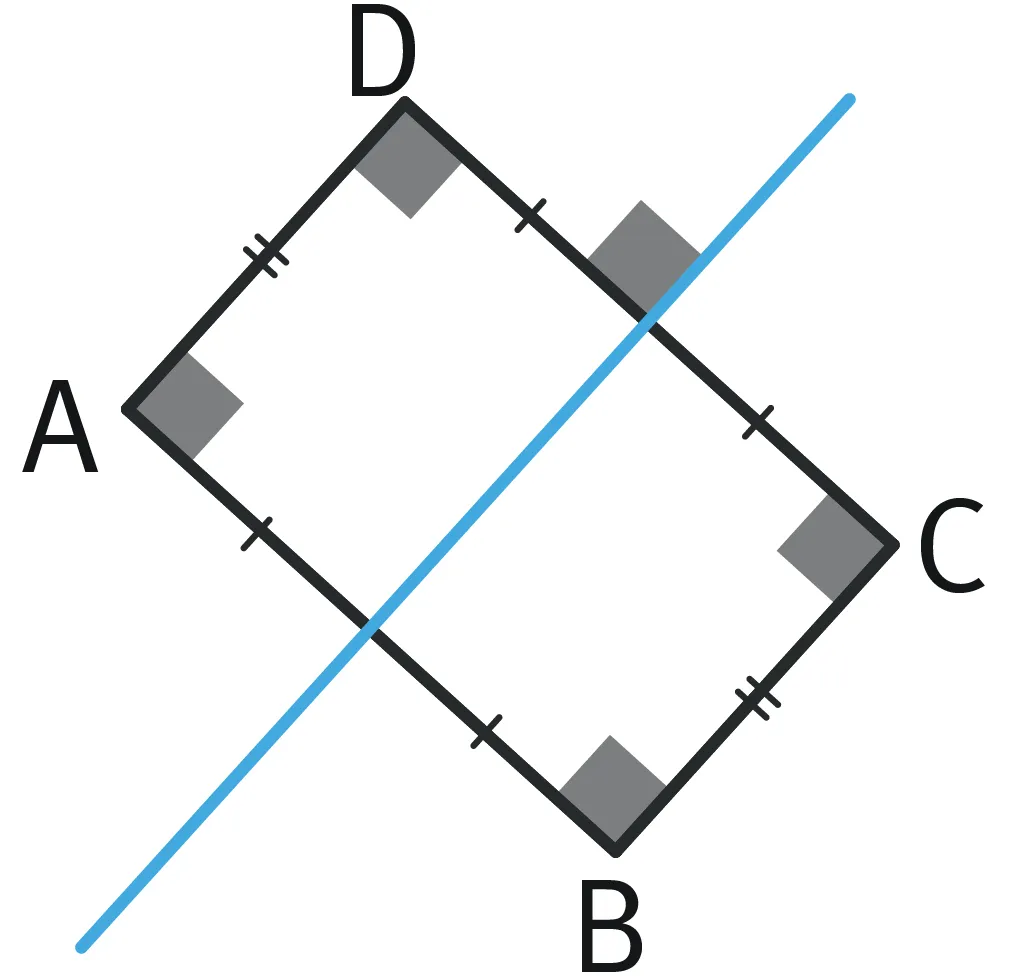
Refaire Étudier les longueurs des côtés d'un rectangle.
- Montrer que AD = BC.
- Dans la symétrie d'axe bleu, B est le symétrique de A et C est le symétrique de D.
- Donc le symétrique de [AD] est [BC].
- Or la symétrie conserve les distances : AD = BC.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7 Dans la figure ci-contre
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
Dans un rectangle, les côtés opposés sont de même longueur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
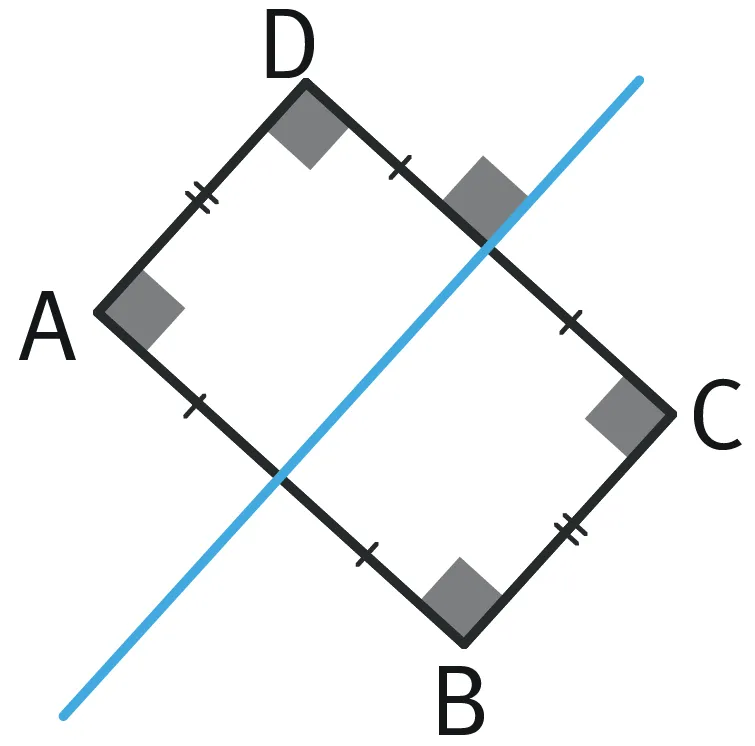
- Dans la symétrie d'axe bleu, B est le symétrique de A et D est le symétrique de C.
- Or la symétrie conserve les distances.
- Ainsi AC = BD.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
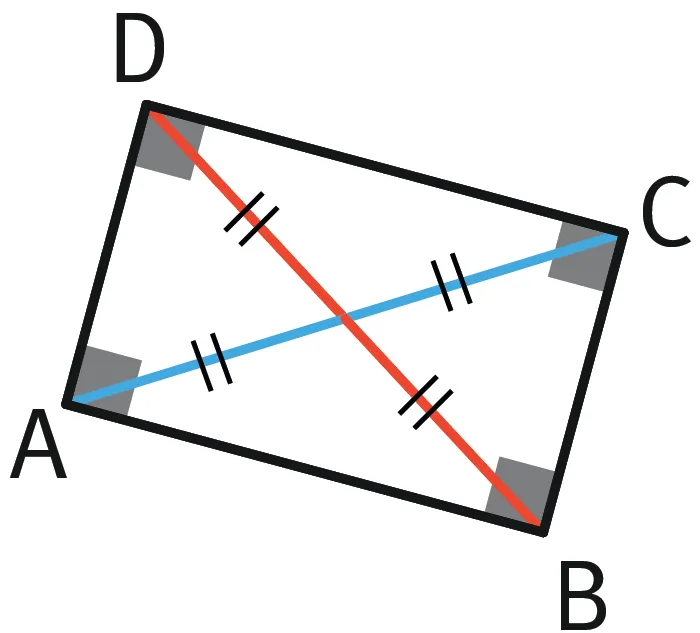
Retenir
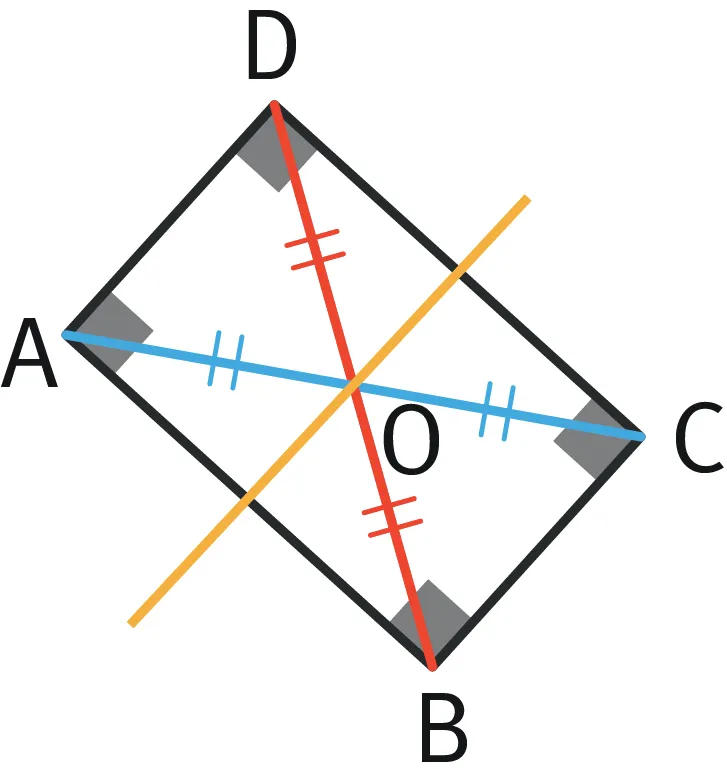
Dans un rectangle ABCD, les segments [BD] et [AC] sont appelés les diagonales. Elles sont de même longueur et se coupent en leur milieu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Remarque :
En général (sauf dans le cas d'un carré), les diagonales d'un rectangle ne sont pas des axes de symétrie.
En général (sauf dans le cas d'un carré), les diagonales d'un rectangle ne sont pas des axes de symétrie.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
Les diagonales et les axes de symétrie d'un rectangle sont tous sécants en un même point.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
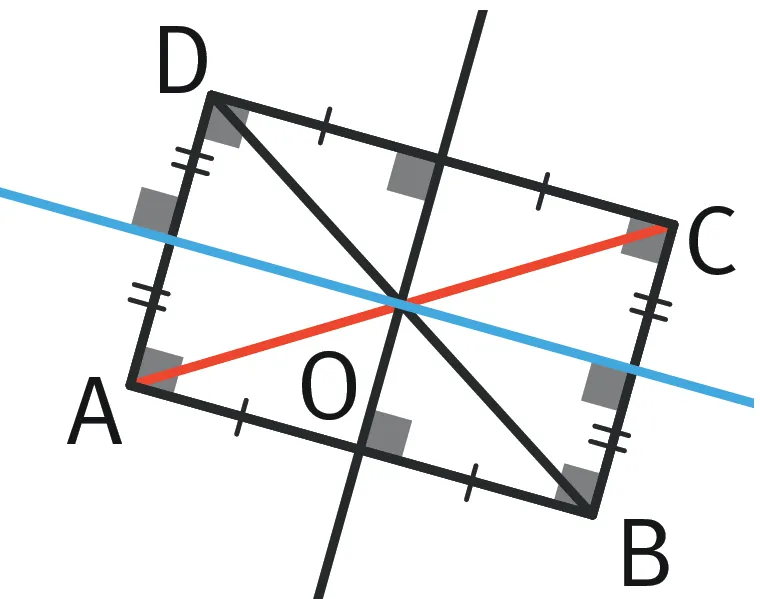
Exemple : O est le point d'intersection des diagonales [AC] et [BD] et des axes de symétrie (les droites rouge et bleue).
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Étudier les diagonales d'un rectangle
- Montrer que OD = OC.
- Dans la symétrie par rapport à la droite orange, O est le symétrique de O et C est le symétrique de D.
- Donc le symétrique de [OD] est [OC].
- Or la symétrie conserve les distances.
- Ainsi OD = OC.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 8 Dans la figure ci-contre
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CCarré
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
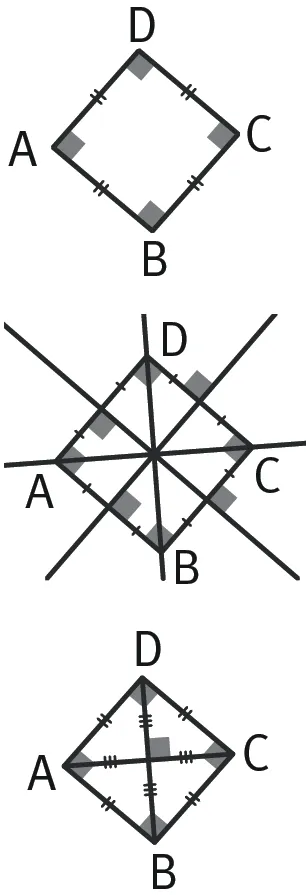
Retenir
- Un carré est à la fois un losange et un rectangle. Tout carré possède donc toutes les propriétés des losanges et des rectangles. Un carré est donc un quadrilatère qui possède :
- quatre angles droits ;
- quatre côtés de même longueur.
- Un carré possède toujours quatre axes de symétrie :
- les deux médiatrices de ses côtés ;
- ses deux diagonales.
- Les diagonales d'un carré sont perpendiculaires, de même longueur et se coupent en leur milieu.
- Les côtés opposés d'un carré sont parallèles.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
DParallélogramme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
Tracer sur une feuille deux droites sécantes et . Construire une droite parallèle à et une autre droite parallèle à . Quelle figure obtient-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
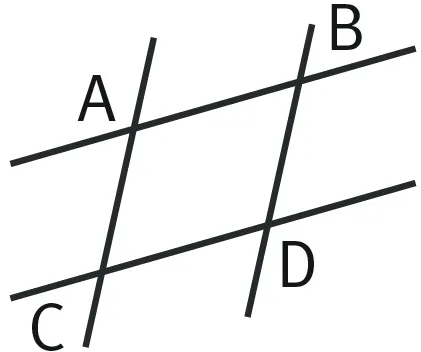
Refaire Sachant que (AB) // (CD), le quadrilatère suivant est-il un parallélogramme ?
- Les droites (AC) et (BC) sont parallèles.
- ABCD est donc bien un parallélogramme.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 9 Parallélogrammes
a.
b.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Sur les figures ci-dessus, les droites forment-elles des parallélogrammes ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarahUtilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.
