Mathématiques 6e
Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Mes Pages
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 11
Pas à pas
1. Propriétés des triangles usuels
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
a. Décalquer les figures suivantes et les recopier sur le cahier.




b. Coder chaque figure en utilisant les instruments de mesure (règle graduée et équerre).
c. Repérer à l'œil nu les axes de symétrie et les tracer pour chaque figure.
d. Regrouper ces figures dans plusieurs catégories, en fonction des observations précédentes. Des figures pourront éventuellement appartenir à plusieurs catégories.
e. Expliquer le choix des catégories. Les élèves de la classe ont-ils tous choisi les mêmes catégories ?
c. Repérer à l'œil nu les axes de symétrie et les tracer pour chaque figure.
d. Regrouper ces figures dans plusieurs catégories, en fonction des observations précédentes. Des figures pourront éventuellement appartenir à plusieurs catégories.
e. Expliquer le choix des catégories. Les élèves de la classe ont-ils tous choisi les mêmes catégories ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
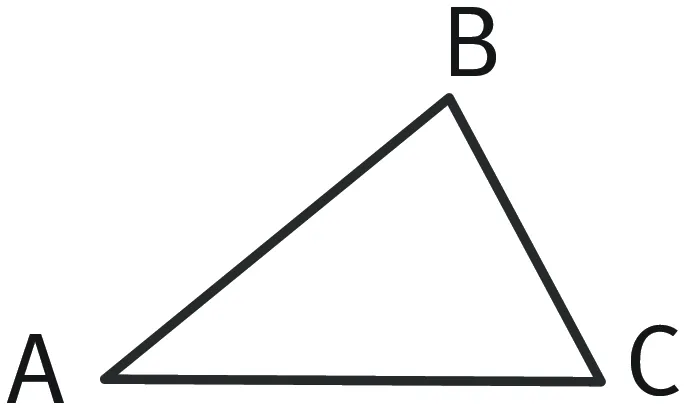
Un triangle est un polygone formé de trois points (les sommets) et de trois côtés. On le désigne souvent par ses sommets.
Remarque :
Un triangle a trois angles, \widehat{\text{BAC}}, \widehat{\text{CBA}} et \widehat{\text{ACB}}.
Remarque :
Un triangle a trois angles, \widehat{\text{BAC}}, \widehat{\text{CBA}} et \widehat{\text{ACB}}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
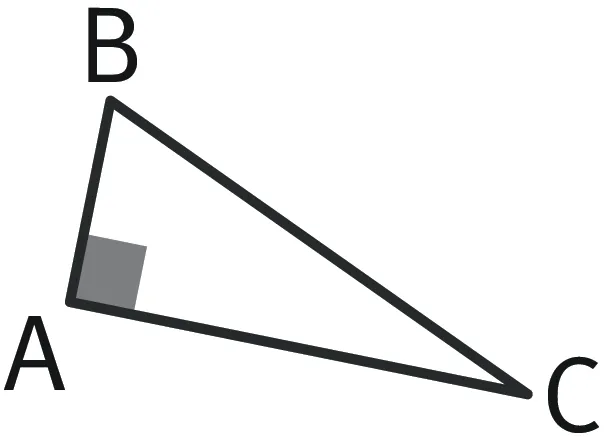
ATriangle rectangle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
- Un triangle rectangle est un triangle possédant un angle droit.
- On dit que le triangle ABC est rectangle en A. Cela permet de savoir où est l'angle droit !
Remarque :
Il ne peut y avoir qu'un seul angle droit dans un triangle.
Remarque :
Ce n'est pas parce qu'un triangle est rectangle qu'il a un (ou des) axes de symétrie.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
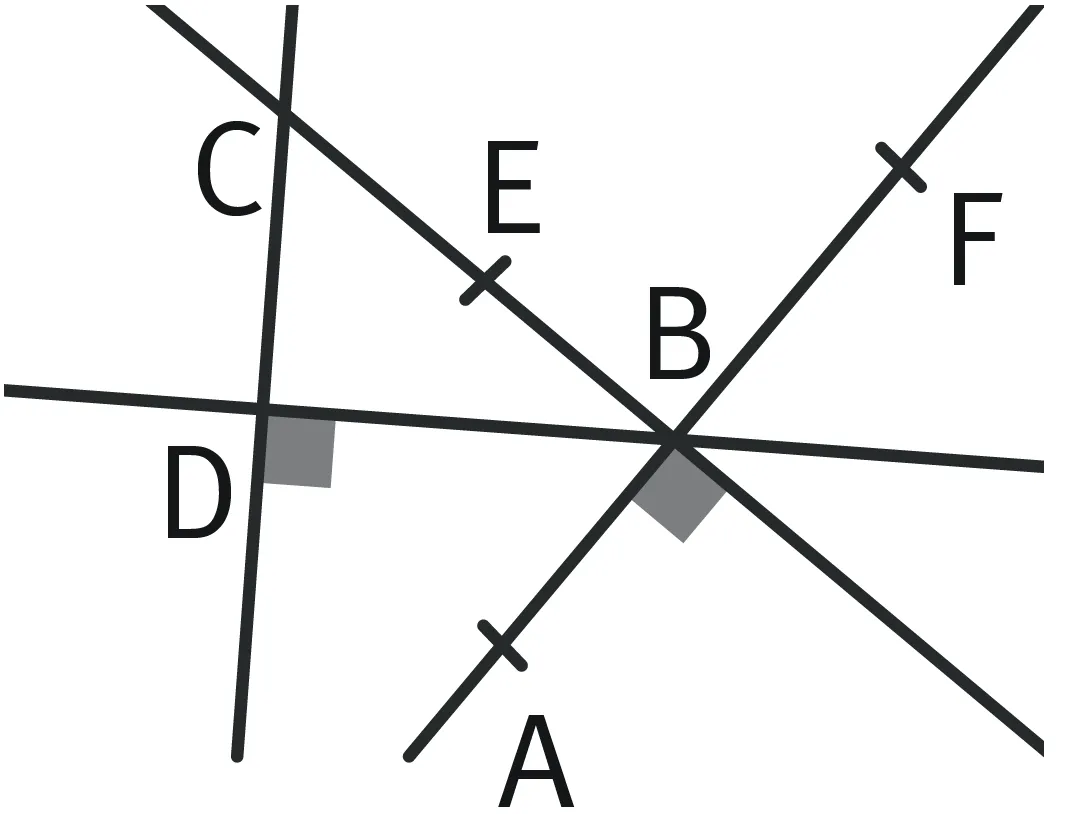
Refaire Repérer des triangles rectangles
Nommer tous les triangles rectangles que l'on peut construire avec les sommets A, B, C, D, E et F.
- On repère les angles droits : ils sont situés sur les points D et B.
- Pour le sommet D, on peut construire le triangle BCD, rectangle en D.
- Pour le sommet B, on peut construire :
- le triangle BCA, rectangle en B ;
- le triangle BEA, rectangle en B ;
- le triangle BCF, rectangle en B ;
- le triangle BEF, rectangle en B.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1Reproduire chaque figure

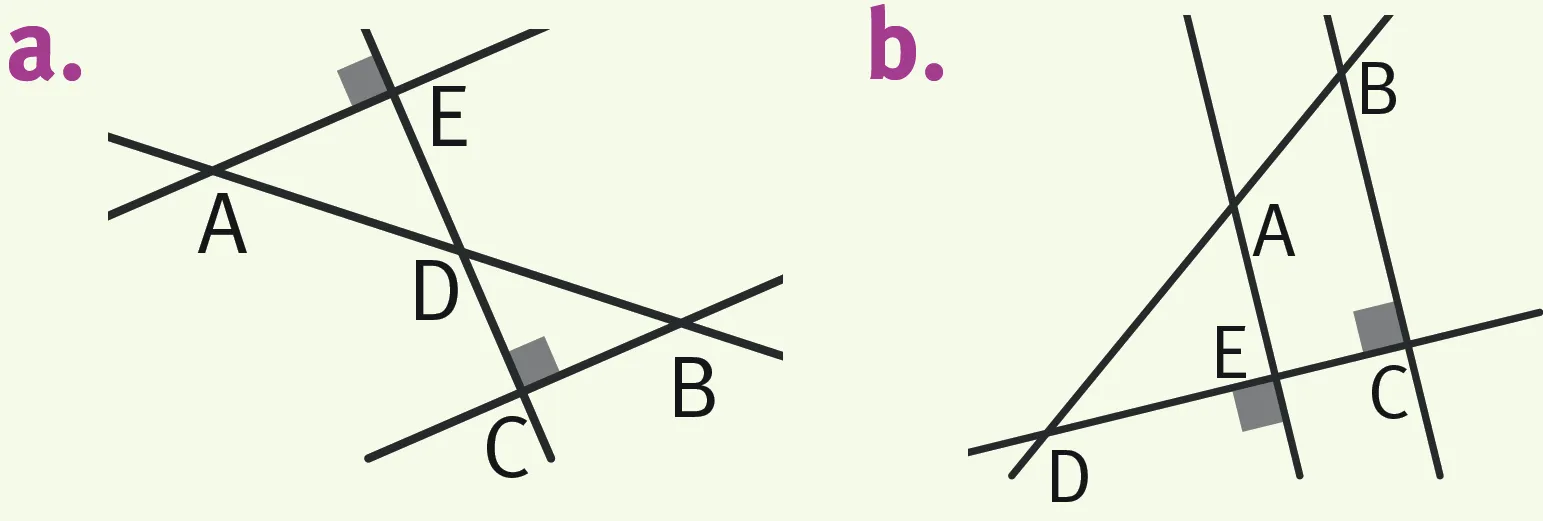
1. Nommer les triangles rectangles qui apparaissent dans la figure a.
2. Nommer les triangles rectangles qui apparaissent dans la figure b.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BTriangle isocèle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
a. En utilisant un logiciel de géométrie dynamique, construire un triangle ABC tel que AB = AC.
b. Tracer la médiatrice de [BC]. Que remarque-t-on ?
c. Afficher les mesures des angles \widehat{\text{ABC}} et \widehat{\text{ACB}}. Que remarque-t-on ?
d. Les propriétés remarquées sont-elles conservées quand on déforme le triangle ?
b. Tracer la médiatrice de [BC]. Que remarque-t-on ?
c. Afficher les mesures des angles \widehat{\text{ABC}} et \widehat{\text{ACB}}. Que remarque-t-on ?
d. Les propriétés remarquées sont-elles conservées quand on déforme le triangle ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
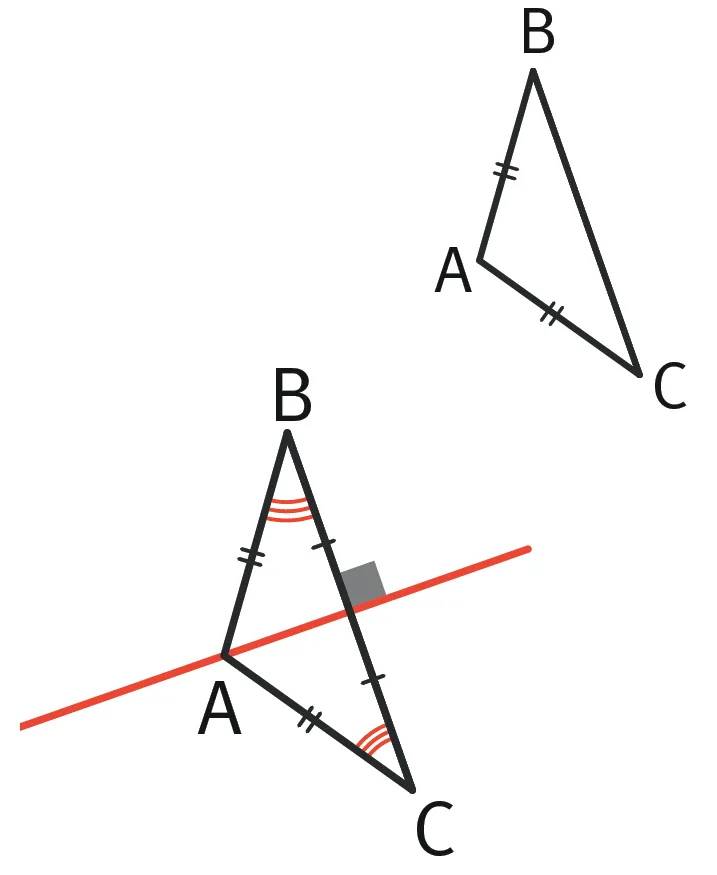
Retenir
- Définition : Un triangle isocèle est un triangle qui possède deux côtés de longueurs égales.
- On dit que le triangle ABC est isocèle en A. Cela veut dire que AB = AC !
- Propriété : Un triangle ABC isocèle en A possède un axe de symétrie : c'est la médiatrice de [BC].
Remarque :
Un triangle isocèle peut parfois posséder plus d'un axe de symétrie, dans ce cas, c'est un triangle équilatéral, mais jamais moins.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
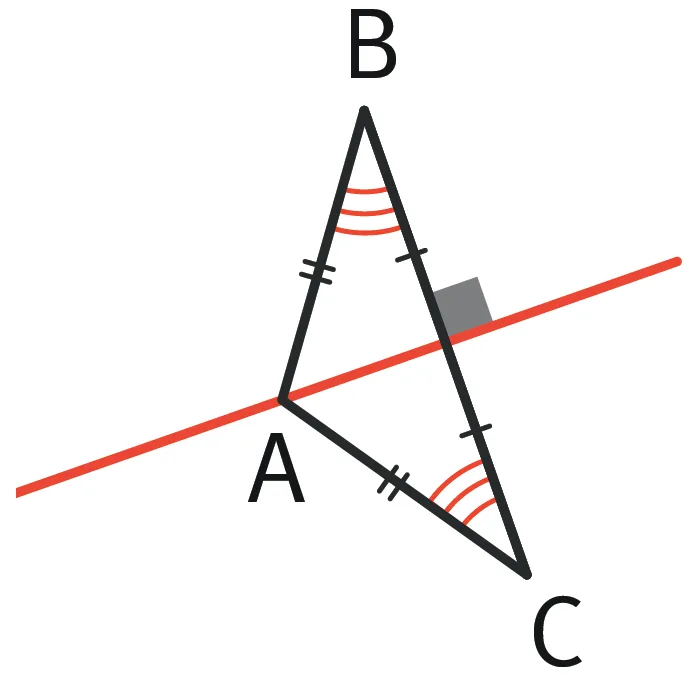
Retenir
- Dans la symétrie par rapport à la droite rouge, A est le symétrique de A et C est le symétrique de B.
- Donc l'angle \widehat{\text{BCA}} est le symétrique de l'angle \widehat{\text{ABC}}.
- On sait que la symétrie conserve les angles.
- On a donc par symétrie : \widehat{\text{ABC}} = \widehat{\text{BCA}}.
- Un triangle isocèle possède deux côtés égaux et deux angles égaux.
- Si un triangle possède deux angles égaux, alors il est isocèle !

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
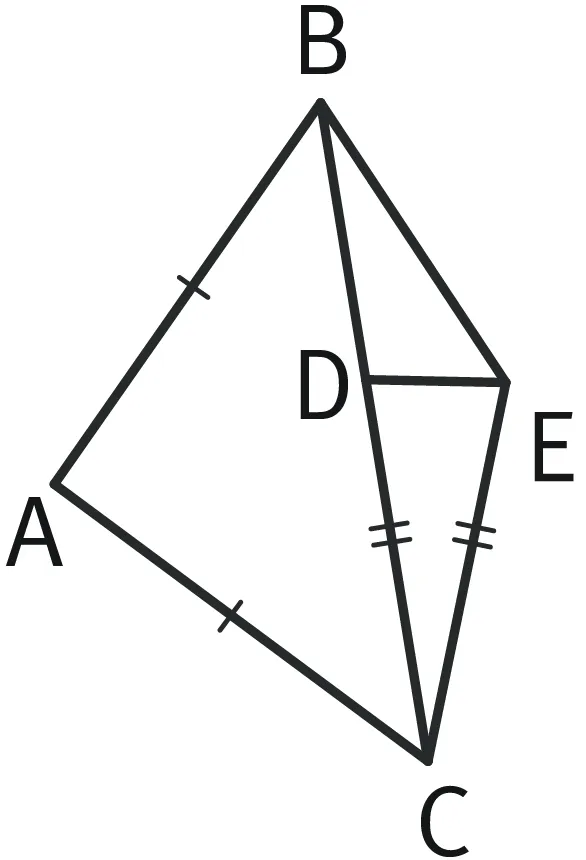
Refaire Repérer des triangles isocèles
Repérer les triangles isocèles dans cette figure et prouver que \widehat{\text{CDE}} = \widehat{\text{DEC}}.
Donc \widehat{\text{CDE}} = \widehat{\text{DEC}}.
- On repère les segments de même longueur : AB = AC et CD = CE.
- Donc ABC est isocèle en A et CDE est isocèle en C.
- Dans le triangle CDE (isocèle en C), les deux angles qui n'ont pas C comme sommet sont égaux.
Donc \widehat{\text{CDE}} = \widehat{\text{DEC}}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2Repérer les triangles isocèles dans cette figure

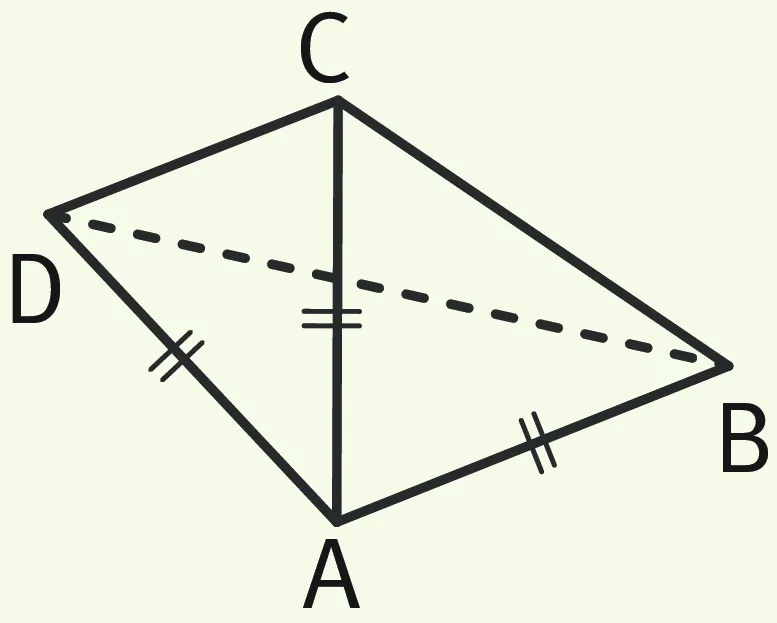
1. Montrer que \widehat{\text{ABD}} = \widehat{\text{BDA}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3Repérer les triangles isocèles dans cette figure

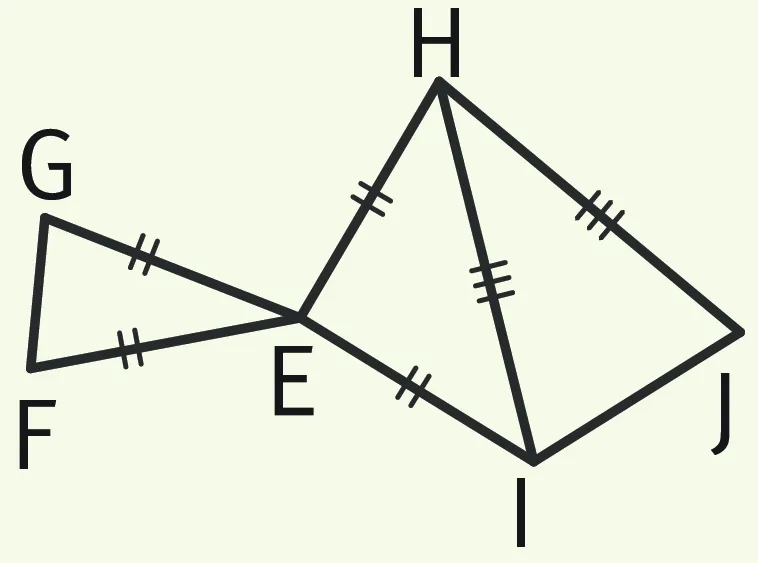
1. Montrer que \widehat{\text{EHI}} = \widehat{\text{HIE}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CTriangle équilatéral


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
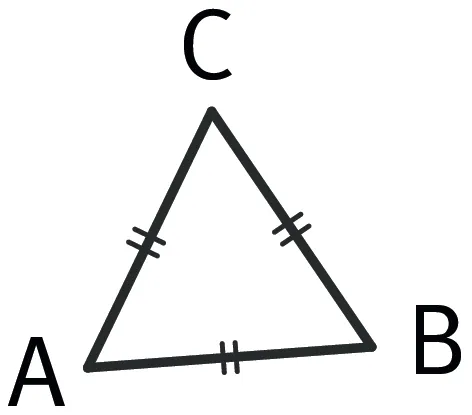
- Un triangle équilatéral est un triangle qui possède trois côtés de même longueur : il est isocèle en chacun de ses sommets.
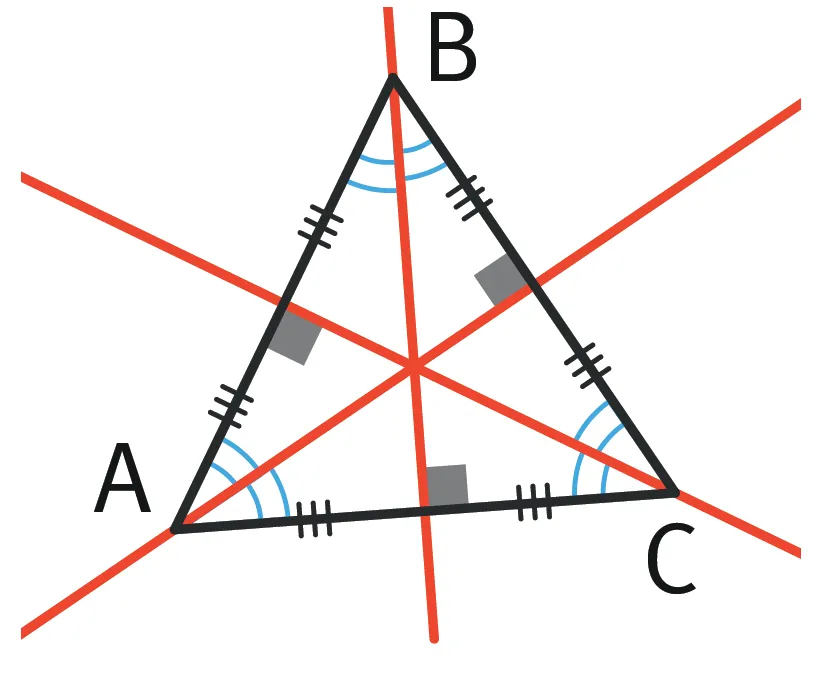
- Propriété : Un triangle équilatéral possède toujours trois axes de symétrie : ce sont les médiatrices de chaque côté.
- Dans ce triangle équilatéral ABC, les trois droites rouges sont les axes de symétrie du triangle.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
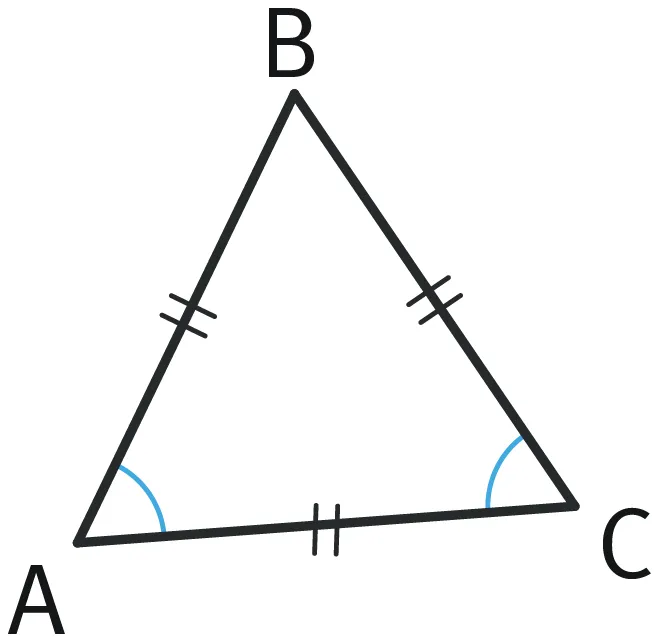
Refaire Étudier les angles d'un triangle équilatéral
Montrer que \widehat{\text{CAB}} = \widehat{\text{BCA}}.
Ainsi \widehat{\text{CAB}} = \widehat{\text{BCA}}.
- Le triangle ABC est isocèle en B.
- Dans un triangle isocèle en B, les deux angles dont le sommet n'est pas B sont égaux.
Ainsi \widehat{\text{CAB}} = \widehat{\text{BCA}}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4Angles

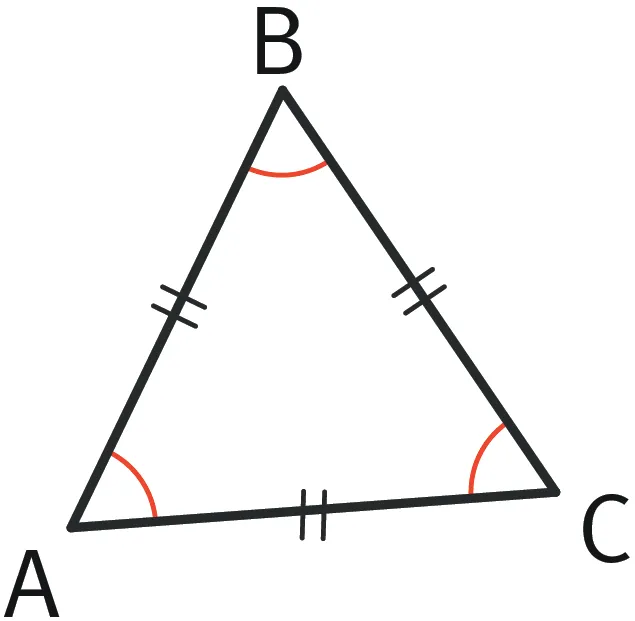
1. Montrer que \widehat{\text{ABC}} = \widehat{\text{BCA}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
Propriété : Les trois angles d'un triangle équilatéral ABC sont égaux.
- \widehat{\text{CAB}} = \widehat{\text{ABC}} = \widehat{\text{ACB}}


Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
