Nos classiques

Mathématiques Cycle 4

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Trigonométrie
Ouverturep. 389
Je découvre le chapitre
Introductionp. 390-391
J'apprends
Coursp. 392-393
Questions Flash / Je m'entraine
Exercicesp. 394-399
Problèmes résolus
Problèmesp. 400
Problèmes résolus
Problèmesp. 401
Je résous des problèmes
Exercicesp. 402-405
Exercices numériques
Exercicesp. 406
Maths autrement : La tête dans les étoiles
Travailler autrementp. 407
Je m'évalue
Exercicesp. 408
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Nos dossiers d'actualité
Dossier d'actualité
Chapitre 18
Exercices

Je résous des problèmes

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

44
Tour Eiffel

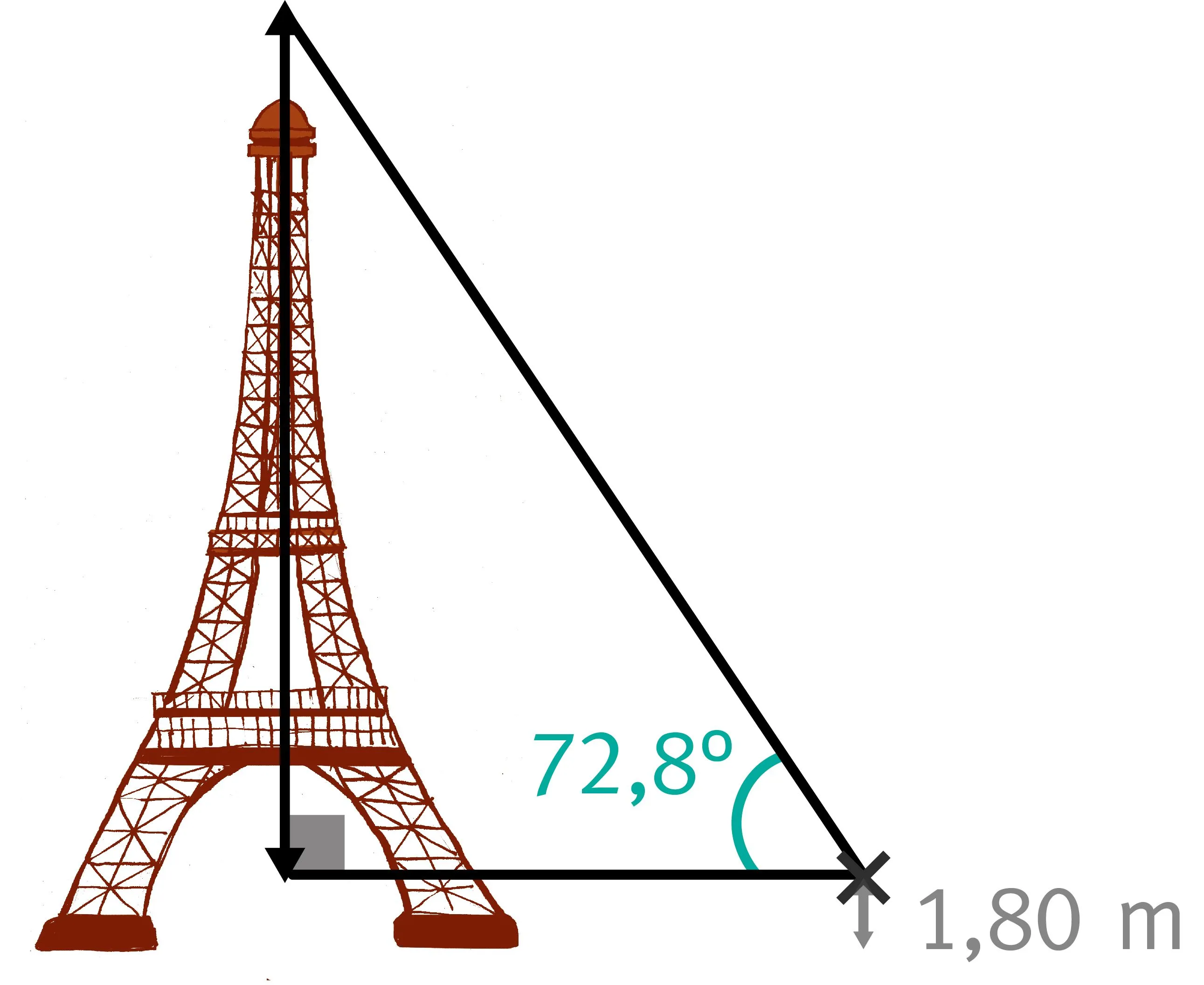
Placeholder pour Schéma illustrant le calcul de la hauteur de la Tour Eiffel : un triangle rectangle avec un angle de 72,8° et une distance de 1,80 m.Schéma illustrant le calcul de la hauteur de la Tour Eiffel : un triangle rectangle avec un angle de 72,8° et une distance de 1,80 m.
Un homme mesurant \text{1,80~m}, placé à \text{100~m} de la tour Eiffel, observe son point culminant avec un angle de \text{72,8}^{\circ}.

Calculez la hauteur de la tour Eiffel.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

45
Un escalier au bout d'une allée

Graphique lié d'un triangle et un escalier
Calculez la longueur \text{ES} de lʼescalier, ainsi que sa hauteur.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

46
La statue de la Liberté

Placeholder pour Dessin stylisé de la Statue de la Liberté, tenant une torche et une tablette. Symbole de liberté et démocratie.Dessin stylisé de la Statue de la Liberté, tenant une torche et une tablette. Symbole de liberté et démocratie.
Figure liée à l'exercice 46
1. Calculez une valeur approchée de la hauteur de la statue de la Liberté, sachant quʼelle correspond à la mesure \text{AE} sur le dessin suivant.
 2. La réplique de la statue de lʼile aux Cygnes à Paris en est une reproduction de rapport \dfrac{1}{4}. Quelle est sa hauteur ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

47
Tyrolienne

Placeholder pour Photographie d'une personne en tyrolienne au-dessus d'une forêt tropicale. Vêtements orange, casque rouge.Photographie d'une personne en tyrolienne au-dessus d'une forêt tropicale. Vêtements orange, casque rouge.
Une tyrolienne permet de se déplacer entre deux arbres. Au parc Aventure du Bugey, la tyrolienne mesure \text{58~m} et fait avec lʼhorizontale un angle de 8^{\circ}. On supposera que la corde est rectiligne.

De quelle distance, arrondie au \text{cm}, sont espacés les deux arbres ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

48
Un ascenseur à bateaux

Le plan incliné de Saint-Louis-Arzviller est un ascenseur à bateaux. Il permet de faire monter et descendre les bateaux le long dʼune rampe inclinée de \text{120~m}. Cette rampe fait un angle de \text{20}^{\circ} avec lʼhorizontale.
Placeholder pour Ascenseur à bateaux de Saint-Louis-Arzviller, structure moderne dans un paysage automnal. Canal calme au premier plan.Ascenseur à bateaux de Saint-Louis-Arzviller, structure moderne dans un paysage automnal. Canal calme au premier plan.
1. Modélisez le problème par une figure.

Cliquez pour accéder à une zone de dessin

2. Calculez le dénivelé (différence entre le point haut et le point bas) de la rampe.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

49
Installation d'une échelle

On pose une échelle de \text{5~m} contre le mur dʼune maison. Lʼéchelle atteint la base du toit à \text{3,50~m} du sol.

1. Quel est lʼangle dʼinclinaison de lʼéchelle par rapport au mur ?
2. À quelle distance du mur la base de lʼéchelle est-elle posée ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

50
Vers le Brevet (Amérique du Sud, 2012)

Deux bateaux sont au large dʼune ile et souhaitent la rejoindre pour y passer la nuit. On peut schématiser leurs positions par les points \text{A} et \text{B}. Ils constatent quʼils sont séparés de \text{800~m} et chacun voit lʼile sous un angle différent.
Figure d'un triangle ABI
1. Démontrez que le triangle est rectangle.
 2. Déterminez, au \text{m} près, la distance qui sépare chaque bateau de lʼile.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

51
Vers le Brevet (Amérique du Nord, 2011)

Figure ABCD
1. Calculez la valeur exacte de \text{BC}.
 2. Calculez lʼarrondi de \text{BD} au mm près.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

52
Pistes noires

Une pente de 70~\% signifie que lʼon perd ou que lʼon gagne \text{70~m} dʼaltitude lorsque lʼon parcourt \text{100~m} à lʼhorizontale. Laure descend une piste noire ayant une pente de 70~\%.

1. Calculez lʼangle dʼinclinaison de la piste.
 2. Calculez la distance réellement parcourue par Laure lorsquʼelle avance de \text{100~m} par rapport à lʼhorizontale.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

53
L'ombre d'Anna

Anna se tient debout au soleil et demande à Mohammed de mesurer son ombre : \text{2,70~m}, règle à lʼappui.

1. À 18 h, on estime que les rayons du soleil forment un angle de \text{30}^{\circ} par rapport au sol. Quelle taille fait Anna ?
 2. Quelle sera la taille de son ombre à midi le 21 juin lorsque les rayons du soleil formeront un angle de 70^{\circ} avec le sol ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

54
La largeur d'une rivière

Un croquis qui figure sur le cahier de M. Schmitt
M. Schmitt, géomètre, doit calculer la largeur dʼune rivière. Voici le croquis qui figure sur son carnet. \text{AB = 100~m} ; \widehat{\text{BAC}} \text{= 25} ^{\circ} ;  \widehat{\text{BAD}} \text{= 70} ^{\circ} ;  \widehat{\text{ABD}} \text{= 90} ^{\circ}.

1. Calculez les longueurs \text{BC} et \text{BD} en arrondissant au dixième.
 2. Déduisez-en la largeur de la rivière représentée par le segment \text{[CD]}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

55

\text{ABC} est un triangle rectangle en \text{B}. Démontrez que (\sin\widehat{\text{BAC}})^{2} + (\cos\widehat{\text{BAC}})^{2} = 1, quelle que soit la mesure des côtés du triangle \text{ABC}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

56

\text{ABC} est un triangle rectangle en \text{B}. Démontrez que \tan\widehat{\text{BAC}} = \sin\widehat{\text{BAC}}\div\cos\widehat{\text{BAC}} pour toute mesure dʼun angle aigu \widehat{\text{BAC}}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

57
Application

\text{ABC} est un triangle rectangle en \text{B}. En utilisant les exercices
55
et
56
, et sachant que \sin \widehat{\text{BAC}} \text{=} \text{0,8}, calculez \cos\widehat{\text{BAC}} et \tan\widehat{\text{BAC}}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

58
Savoir refaire

Quelle est la hauteur dʼune pyramide régulière dont la base est un carré de côté \text{50~m} et dont lʼangle dʼinclinaison est de \text{42} ^{\circ} ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

59
Pyramide de base carrée

\text{SABCD} est une pyramide régulière de base carrée de \text{7~cm} de côté. Lʼangle \widehat{\text{SAC}} mesure \text{51}^{\circ}.

1. Calculez la hauteur de la pyramide arrondie au \text{mm}.
 2. Déduisez-en son volume au \text{cm}^{3} près.
 3. Calculez la longueur des arêtes \text{[SA]}, \text{[SB], [SC], [SD]}.
 4. Tracez le triangle \text{SAB}. Quelle est sa nature ?

Cliquez pour accéder à une zone de dessin

5. Sur la face \text{SAB}, on appelle \text{H} le pied de la hauteur issue de \text{A} et relative à \text{[AB]}. Déterminez la longueur de \text{SH}.
 6. Calculez lʼaire totale de la surface de la pyramide.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

60
Les diagonales d'un parallélépipède rectangle

Graphique d'un parallélépipède rectangle ABCDHEFG
Dans le parallélépipède rectangle \text{ABCDHEFG}, \text{AB = 1~cm}, \text{AD = 1~cm} et \text{AE = 2~cm}.
I est le point dʼintersection des diagonales \text{(AG)} et (\text{C}\text{E}).

Calculez la mesure de l'angle \widehat{\text{EIA}}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

61
Vider un bac

Graphique d'un bac parallélépipédique
Un bac parallélépipédique de \text{12~cm} de hauteur, \text{20~cm} de longueur et \text{8~cm} de largeur est rempli aux deux tiers dʼeau.

Alice lʼincline sur la largeur pour le vider. Elle se demande à quel moment lʼeau va se déverser dans lʼévier. Quʼen pensez-vous ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

62
Rampe d'accès

On souhaite construire une rampe dʼaccès pour les personnes à mobilité réduite qui souhaitent accéder à lʼentrée du collège. Cette rampe mesure \text{10~m} et le seuil de la porte est situé à \text{50~cm} du sol.

1. Modélisez le problème par une figure.

Cliquez pour accéder à une zone de dessin

2. Calculez la mesure de lʼangle fait par la rampe (arrondie au degré).
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

63
Constructions

1. Tracez le triangle rectangle \text{ABC} rectangle en \text{B} tel que \text{AB = 4~cm} et \cos\widehat{\text{BAC}} \text{= 0,8}.

Cliquez pour accéder à une zone de dessin

2. Tracez un triangle \text{A'B'C'} semblable à ce triangle avec \text{A'B' = 8~cm}.

Cliquez pour accéder à une zone de dessin

3. Combien vaut \cos\widehat{\text{B}^{\prime}\text{A}^{\prime}\text{C}^{\prime}}  ?
4. Comparez \sin\widehat{\text{BAC}} et \sin\widehat{\text{B}^{\prime}\text{A}^{\prime}\text{C}^{\prime}}. Que remarquez-vous ?
 5. Pouvez-vous relier cela avec un théorème vu dans un précédent chapitre ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

64
Vers le Brevet (Amérique du Nord, 2013)

Le Pentagone est un bâtiment qui héberge le ministère de la Défense des États-Unis. Il a la forme dʼun pentagone régulier inscrit dans un cercle de rayon \text{OA = 238~m}. Il est représenté par le schéma suivant.
Graphique d'un pentagone régulier
1. Calculez la mesure de lʼangle \widehat{\text{AOB}}.
 2. La hauteur issue de \text{O} dans le triangle \text{AOB} coupe le côté \text{[AB]} au point \text{M}.
a. Justifiez que \text{(OM)} coupe \widehat{\text{AOB}} en deux angles égaux et est la médiatrice de \text{[AB]}.
 b. Prouver que \text{[AM]} mesure environ \text{140~m}.
 c. Déduisez-en une valeur approchée du périmètre du Pentagone.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

65
Tour de Pise

Le côté de la tour \text{[SE]} mesure \text{55,86~m}. On cherche à connaitre lʼangle dʼinclinaison α de la tour de Pise. Pour cela, on se place sous le sommet \text{S} de la tour, on recule de \text{50~m} et on regarde le sommet avec un angle de \text{48,1}^{\circ}.
Graphique de la tour de Pise
Calculez lʼangle dʼinclinaison de la tour.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

66
Jouer au billard

Le rectangle suivant représente une table de billard. Deux boules de billard \text{N} et \text{B} sont placées telles que : \text{CD = 70~cm} ; \text{NC = 15~cm} ; \text{BD = 25~cm}. Un joueur veut toucher la boule \text{N} avec la boule \text{B} en suivant le trajet \text{B}, puis \text{E}, puis \text{N}, \text{E} étant entre \text{C} et \text{D}, et tel que la mesure de lʼangle \widehat{\text{CEN}} est égale à celle de \widehat{\text{DEB}}. On pose \text{ED =} a.
Graphique d'un rectangle qui représente une table de billard
1. a. Donnez un encadrement de a.
 b. Exprimez \text{CE} en fonction de a.
2. Dans le triangle \text{BED}, exprimez \tan\widehat{\text{DEB}} en fonction de a.
 3. Dans le triangle \text{NEC}, exprimez \tan\widehat{\text{CEN}} en fonction de a.
 5. Écrivez une égalité liant les deux quotients trouvés aux questions a et b et écrivez lʼéquation qui en découle.
 6. Résolvez l'equation.
Coup de pouce
Lʼéquation à résoudre est 25(70-a)=15 a
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Exercice numérique

Roméo (point \text{R}) souhaite rejoindre, à l'aide d'une échelle de longueur 3{,}10 \text{m}, Juliette (point \text{J}) qui se trouve tout en haut d'une tour.
Figure d'un triangle
Roméo souhaite que l'angle formé par l'échelle et le sol soit de 46^{\circ}. Quelle doit être la longueur \text{TR} ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Exercice numérique

Roméo (point \text{R}) souhaite rejoindre, à l'aide d'une échelle de 3{,}10 \text{m}, Juliette (point \text{J}) qui se trouve tout en haut d'une tour.
Figure d'un triangle
L'angle formé entre le sol et l'échelle est de 35^{\circ}. Déterminer la hauteur à laquelle se trouve Juliette.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Tâche complexe
Pont suspendu

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

On veut construire un pont suspendu en corde et en bois entre les deux cotés dʼun ravin.

Combien de morceaux de bois faut-il ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 1
La situation

Armand et Théo se tiennent au bord du ravin, et regardent un rocher situé au bord, de l'autre côté. Ils sont séparés l'un de l'autre de \text{110,4 m}.
Graphique lié à l'exercice 1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 2
Caractéristiques du pont

Le pont est constitué de deux cordes tenant des morceaux de bois de \text{15~cm} de large, espacés de \text{20~cm} chacun, et de deux cordes pour se tenir.
Graphique lié à l'exercice 2
Attention
Un pont en corde n'est pas droit, sa longueur doit donc être 15 \% plus grande que la distance qu'il doit couvrir.
 

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.