Mathématiques 6e
Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Mes Pages
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 1
Pas à pas
2. Multiples et diviseurs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ANotion de diviseur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
a. Effectuer de tête les divisions entières de 2, 4, 6 et 8 par 2. Qu'observe-t-on ?
b. Poser la division euclidienne de 4 112 par 3. Qu'observe-t-on ? Et pour la division euclidienne de 4 112 par 2 ?
b. Poser la division euclidienne de 4 112 par 3. Qu'observe-t-on ? Et pour la division euclidienne de 4 112 par 2 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
Un entier b est un diviseur d'un autre entier a lorsque le reste de la division euclidienne de a par b vaut zéro. On dit aussi que a est un multiple de b ou que a est divisible par b.
Remarque :
Quand un nombre vaut zéro, on dit qu'il est nul.
Remarque :
Quand un nombre vaut zéro, on dit qu'il est nul.
Remarque :
Si b divise a, a est un multiple de b et il existe donc un entier q tel que a = b \times q. Par exemple, 3 divise 12 et 12 = 4 \times 3.
Remarques :
Si b divise a, a est un multiple de b et il existe donc un entier q tel que a = b \times q. Par exemple, 3 divise 12 et 12 = 4 \times 3.
Remarques :
- 0 est divisible par tous les nombres entiers : si n est un nombre entier, {0 = n \times 0}.
- 1 est divisible uniquement par 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Vérifier si un nombre est un diviseur d'un autre nombre
Le nombre 7 divise-t-il les nombres suivants ? 25 et 42.
- Posons la division euclidienne de 25 par 7.
- Elle donne un quotient de 3 et un reste de 4.
7 ne divise donc pas 25. - Posons la division euclidienne de 42 par 7.
- Elle donne un quotient de 6 et un reste de 0.
7 est donc un diviseur de 42 et 42 = 6 × 7.

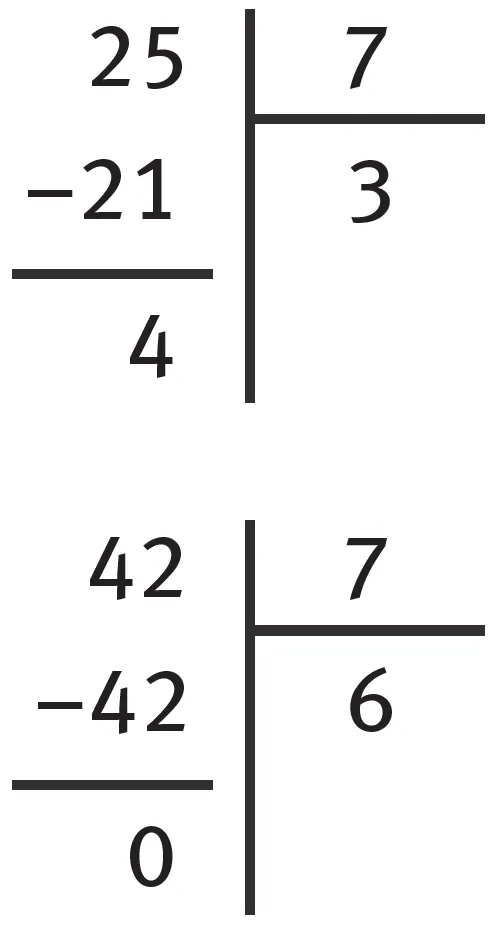
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BCritère de divisibilité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
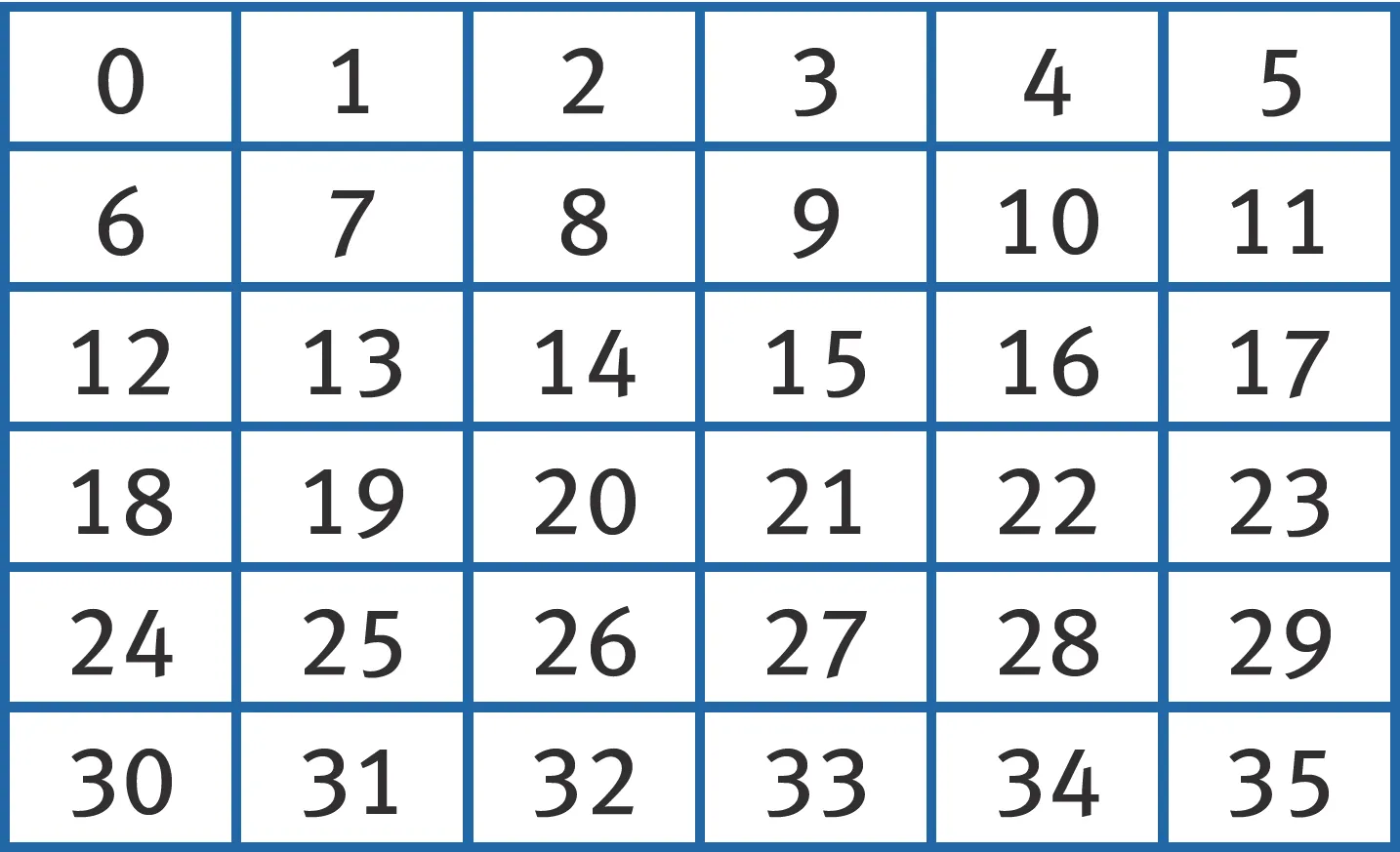
Dans le tableau suivant, entourer en bleu les multiples de 2, en rouge ceux de 5 et en vert ceux de 10.
Remarque :
Pour étudier la divisibilité de nombres simples, on peut effectuer la division entière et voir si le reste est nul. Pour des grands nombres, c'est plus compliqué ! On peut alors utiliser les critères suivants.
Remarque :
Pour étudier la divisibilité de nombres simples, on peut effectuer la division entière et voir si le reste est nul. Pour des grands nombres, c'est plus compliqué ! On peut alors utiliser les critères suivants.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
- Un nombre divisible par 2 est appelé nombre pair. Un nombre entier est divisible par 2 si son dernier chiffre est 0, 2, 4, 6 ou 8.
- 74 est divisible par 2 alors que 75 ne l'est pas.
- Un nombre entier est divisible par 5 si son dernier chiffre est 0 ou 5.
- 595 est divisible par 5 alors que 778 ne l'est pas.
- Un nombre entier est divisible par 10 si son dernier chiffre est 0.
- 450 est divisible par 10 alors que 7 758 ne l'est pas.
- Un nombre entier est divisible par 3 si la somme de ses chiffres est un multiple de 3.
- On additionne les chiffres de 612 : 6 + 1 + 2 = 9 = 3 \times 3.
9 est divisible par 3 alors 612 est aussi divisible par 3. - On additionne les chiffres de 599 : 5 + 9 + 9 = 23.
On veut maintenant savoir si 23 est divisible par 3. On additionne les chiffres de 23 : 2 + 3 = 5. Comme 5 n'est pas divisible par 3 alors 599 ne l'est pas non plus.
- Un nombre entier est divisible par 9 si la somme de ses chiffres est un multiple de 9.
- On additionne les chiffres de 513 : 5 + 1 + 3 = 9. Comme 9 est divisible par 9, 513 l'est aussi.
- On additionne les chiffres de 731 : 7 + 3 + 1 = 11. Comme 11 n'est pas divisible par 9, 731 ne l'est pas non plus.
- Un nombre entier est divisible par 4 si ses deux derniers chiffres forment un nombre divisible par 4.
- On prend les deux derniers chiffres de 1 479 568 qui sont 6 et 8. Si l'on effectue la division de 68 par 4, on obtient un reste nul : 1 479 568 est donc divisible par 4.
- On considère les deux derniers chiffres de 848 945. Si l'on effectue la division de 45 par 4, on obtient 45 = (4 \times 11) + 1. 848 945 n'est donc pas divisible par 4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Utiliser les critère de divisibilité
- Les nombres 42 et 43 sont-ils divisibles par 2 ?
- On regarde le dernier chiffre de ces deux nombres. Pour 42 c'est 2. Donc 42 est divisible par 2 (42 = 2 \times 21). Pour 43 c'est 3. Donc 43 n'est pas divisible par 2.
- Les nombres 39 et 40 sont-ils divisibles par 3 ?
- La somme des chiffres de 39 vaut 3 + 9 = 12. La somme des chiffres de 12 vaut 1 + 2 = 3. On sait donc que 12 est divisible par 3 et 39 l'est aussi (39 = 3 \times 13). La somme des chiffres de 40 est 4 + 0 = 4, qui n'est pas divisible par 3. Donc 40 n'est pas divisible par 3.
- Les nombres 2 196 et 2 198 sont-ils divisibles par 4 ?
- Les deux derniers chiffres de 2 196 et 2 198 forment 96 et 98. La division euclidienne de 96 par 4 donne un reste de 0 (en effet 96 = 4 \times 24) et celle de 98 par 4 donne un reste de 2 (on a 98 = 4 \times 24 + 2). Seul 2 196 est divisible par 4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4Les nombres suivants sont-ils des multiples de 2, 5, 10, 3, 9, ou 4 ?
1. 8
2. 45
3. 20
4. 8 754
5. 666
6. 8 280
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5Donner tous les diviseurs des nombres suivants
1. 8
2. 15
3. 22
4. 27
5. 17
6. 42
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
