Mathématiques 6e
Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Mes Pages
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 1
Pas à pas
1. Division entière
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADivision entière ou division décimale ?
Lorsque l'on effectue une division de nombres entiers, il faut savoir où s'arrêter.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Quand on effectue la division entière de 19 par 6, on garde des nombres entiers.
a. 19 est-il un multiple de 6 ?
b. En cours de sport, les 19 élèves d'une classe de 6e doivent se répartir en groupes de 3. Combien y aura-t-il de groupes ? Restera-t-il des élèves seuls ?
a. 19 est-il un multiple de 6 ?
b. En cours de sport, les 19 élèves d'une classe de 6e doivent se répartir en groupes de 3. Combien y aura-t-il de groupes ? Restera-t-il des élèves seuls ?

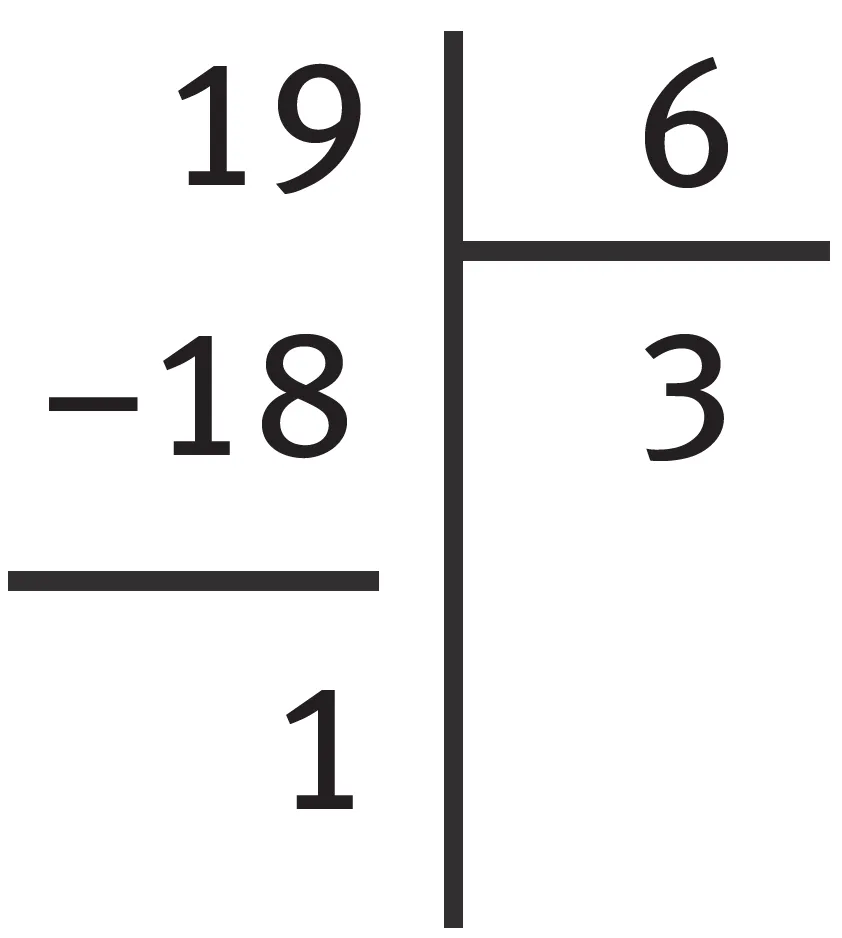
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On effectue la division de 19 par 6 en s'arrêtant aux centièmes.
a. Donner la valeur approchée de 19 ÷ 6 au centième près.
b. La grand-mère de Matthieu a fait 19 kg de confiture et veut les répartir équitablement entre ses 6 petits-enfants. Donner la masse de confiture que recevra chaque petit enfant, au gramme près.
a. Donner la valeur approchée de 19 ÷ 6 au centième près.
b. La grand-mère de Matthieu a fait 19 kg de confiture et veut les répartir équitablement entre ses 6 petits-enfants. Donner la masse de confiture que recevra chaque petit enfant, au gramme près.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BDivision entière
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
Une vendeuse de limonade veut remplir des bouteilles de 33 cl avec un fût de 75 l (soit 7 500 cl).
a. Peut-elle remplir 226 bouteilles ? 227 ? 228 ?
b. Quel est donc le nombre maximal de bouteilles qu'elle pourra servir ?
c. Combien de centilitres de limonade restera-t-il dans le fût ?
d. Quelle opération faut-il faire pour obtenir 7 500 à partir de 9 ? 227 ? 33 ?
a. Peut-elle remplir 226 bouteilles ? 227 ? 228 ?
b. Quel est donc le nombre maximal de bouteilles qu'elle pourra servir ?
c. Combien de centilitres de limonade restera-t-il dans le fût ?
d. Quelle opération faut-il faire pour obtenir 7 500 à partir de 9 ? 227 ? 33 ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir

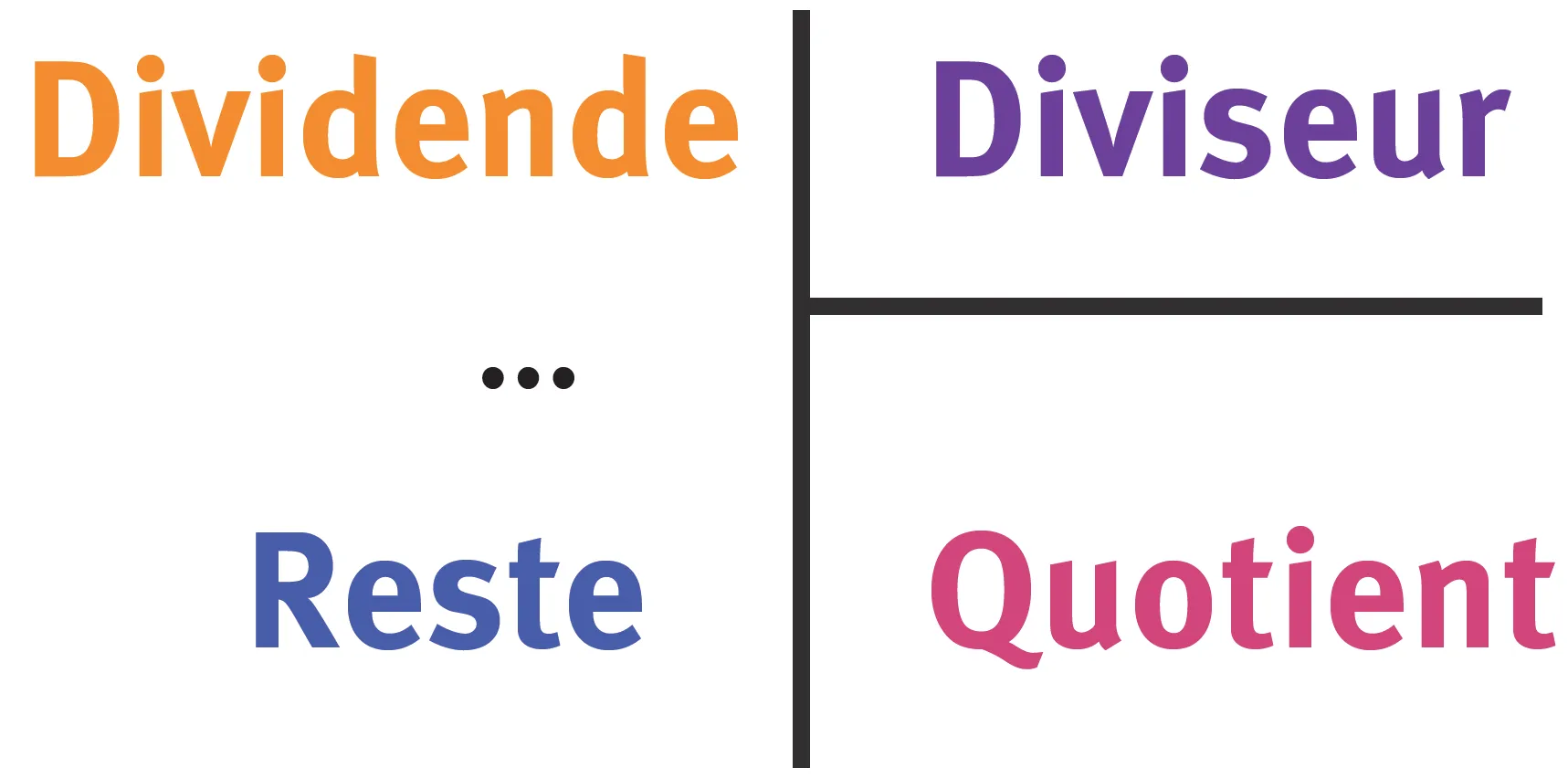
- Pour effectuer la division entière d'un nombre entier (le dividende) par un autre nombre entier (le diviseur), il faut trouver deux nombres entiers (le quotient entier et le reste entier) tels que :
- dividende = (quotient × diviseur) + reste et le reste est plus petit que le diviseur.
- Dans une division euclidienne, il n'y a pas de virgule !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple : La division entière de 7 500 par 33 donne un quotient de 227 et un reste de 9.
Remarque :
Le résultat d'une division entière est toujours constitué de deux nombres entiers : on dit que c'est un couple d'entiers. On ne peut l'appliquer qu'aux nombres entiers : on ne peut pas faire la division entière d'un nombre décimal par un entier !
Remarque :
On appelle aussi la division entière « division euclidienne ».
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Résoudre un problème faisant intervenir une division entière
« Le papa de Roman veut diviser une étagère mesurant 100 cm avec des petites cloisons d'épaisseur négligeable pour former des compartiments de 9 cm de large. Combien de compartiments peut-il faire rentrer ? Va-t-il rester de la place ? Si c'est le cas, combien ? »
- On veut savoir combien de fois faire rentrer 9 cm dans 100 cm. La réponse doit consister en deux nombres entiers : le nombre de compartiments et la place restante (en cm).
- Les données en jeu sont la taille de l'étagère (100 cm) et la taille d'une boite (9 cm).


- On est dans une situation de division entière : on veut effectuer la division entière de 100 par 9.
- On pose l'opération.
- Le quotient de la division entière de 100 par 9 est 11, le reste est 1.
- Le papa de Roman peut donc former 11 cloisons dans l'étagère. Il restera un espace de 1 cm sur l'étagère.
On choisit ici d'effectuer une division entière et non une division décimale car on attend un quotient entier : c'est le nombre de compartiments.

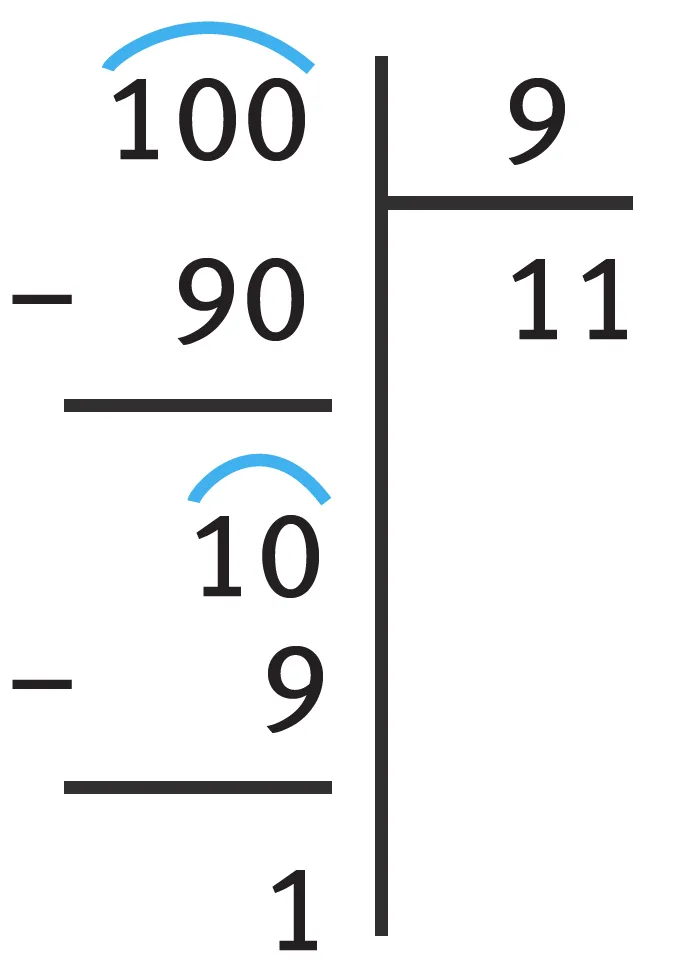
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1Pour chacune des divisions
Indiquer quel nombre est le dividende, le diviseur, le quotient et le reste. Donner ensuite l'écriture en ligne de la division.
| Dividende | Diviseur | Quotient | Reste | Division en ligne | |
|---|---|---|---|---|---|
| a. |
|
|
|
|
|
| b. |
|
|
|
|
|
| c. |
|
|
|
|
|
| d. |
|
|
|
|
|


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2Compléter le tableau
| Dividende | Diviseur | Quotient | Reste |
| 35 | 6 |
|
|
| 41 | 13 |
|
|
| 79 | 4 |
|
|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3Répondre aux questions suivantes
1. Pénélope a 35 bonbons et veut donner autant de ses bonbons à 8 de ses amis. Combien de bonbons peut-elle donner à chacun de ses amis ? Combien lui en reste-t-il pour elle ?
2. Le papa d'Irfane doit déménager 49 cartons. Sa voiture ne peut en contenir que 12 à la fois. Combien de trajets doit-il faire au minimum ? La voiture sera-t-elle pleine à chaque trajet ?
2. Le papa d'Irfane doit déménager 49 cartons. Sa voiture ne peut en contenir que 12 à la fois. Combien de trajets doit-il faire au minimum ? La voiture sera-t-elle pleine à chaque trajet ?


Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
