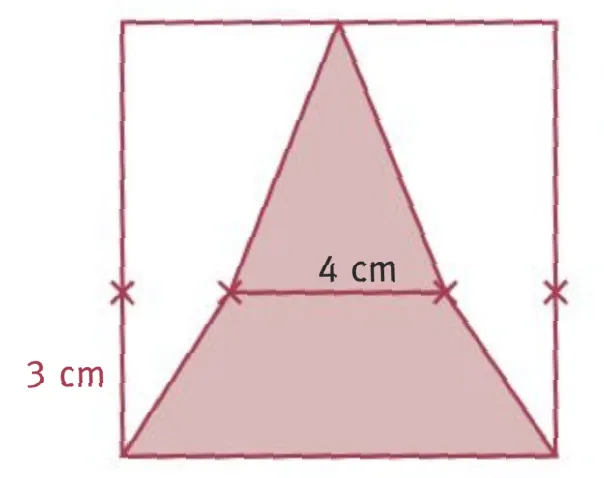
À lʼintérieur dʼun carré de côté 8 cm, on a dessiné une figure composée dʼun trapèze isocèle et dʼun triangle isocèle.

Quelle est lʼaire de ce polygone ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 1

Pour calculer lʼaire dʼune figure incluse dans une autre figure, il est possible de partir de lʼaire de la figure englobante et, ensuite de soustraire à cette aire celles des figures qui nʼappartiennent pas à la figure étudiée.

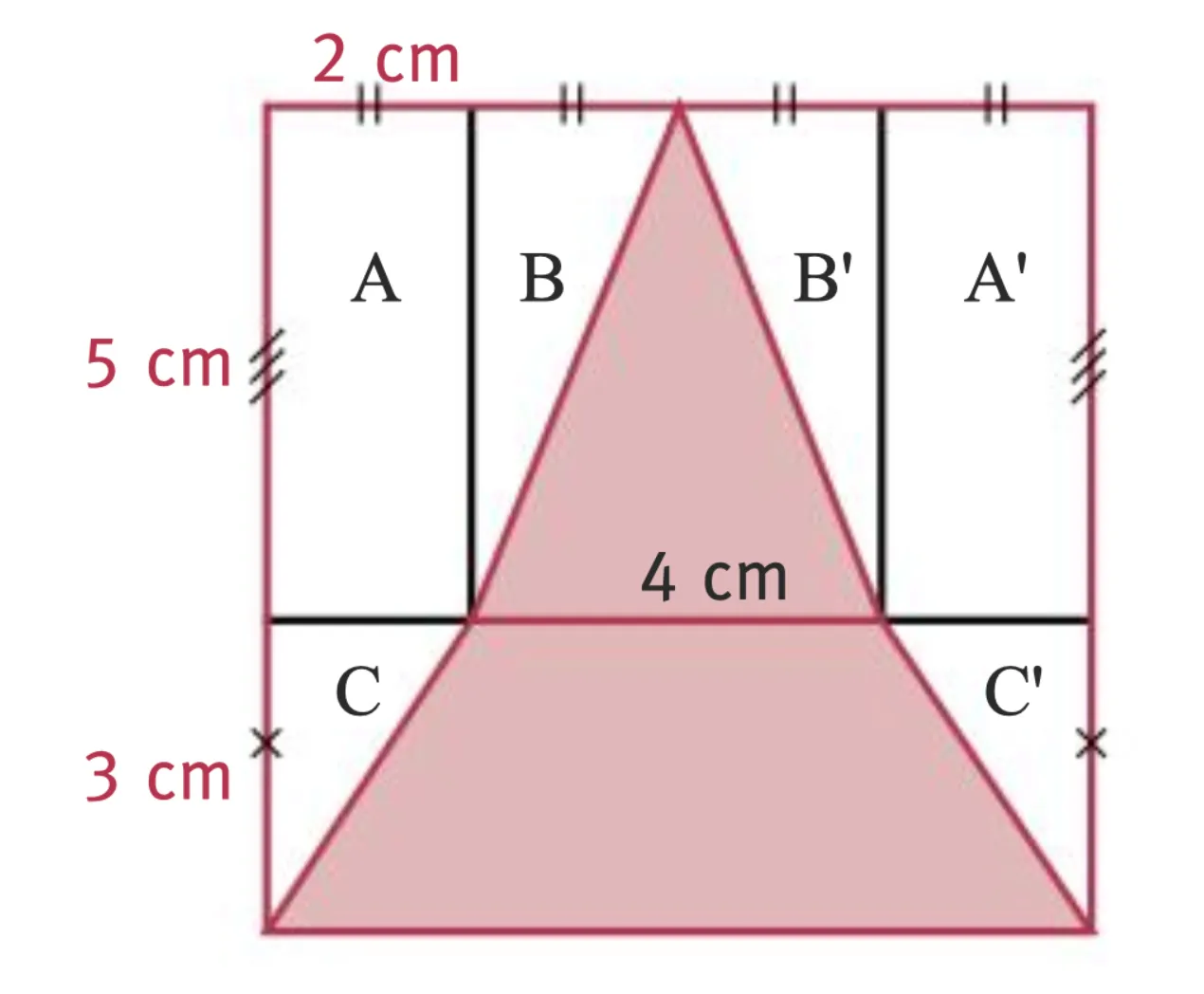
Corrigé 1

Schéma : triangle isocèle dans un carré, côtés mesurés (2, 3, 4, 5 cm).

Aire du carré en cm^2 : 8 \times 8 = 64
Les rectangles \text{A} et \text{A'} ont la même aire, en cm^2 : 2 \times 5 = 10
Les triangles rectangles \text{B} et \text{B'} ont la même aire, en cm^2 : 2 \times 5 \div 2 = 5
Les triangles rectangles \text{C} et \text{C'} ont la même aire, en cm^2 : 2 \times 3 \div 2 = 3
64 - 2 \times 10 - 2 \times 5 - 2 \times 3 = 28

Donc lʼaire de la figure est de 28 cm^2.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 2

Pour calculer lʼaire dʼune figure, il est possible de la diviser en figures dont on connait les formules dʼaires. On calcule alors les aires de chaque figure et on les additionne pour donner lʼaire de la figure cherchée.

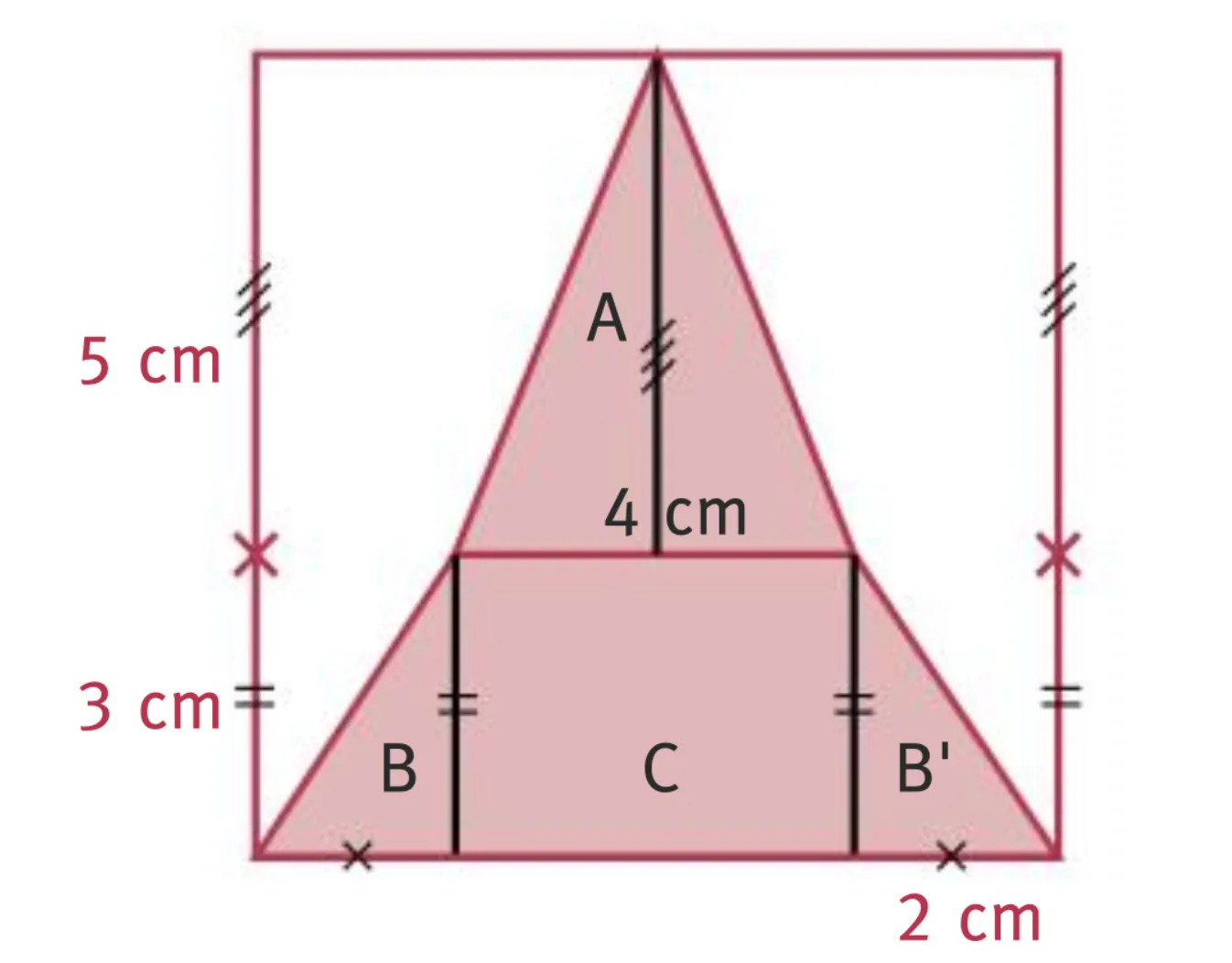
Corrigé 2

Schéma : triangle isocèle dans un carré, segments (A, B, B', C) mesurant 4, 3, 2 cm.

Aire du triangle \text{A} de hauteur 5 cm et de base 4 cm, en cm^2 :
5 \times 4 \div 2 = 10
Les triangles rectangles \text{B} et \text{B'} ont la même aire, en cm^2 :
2 \times 3 \div 2 = 3
Aire du rectangle \text{C}, en cm^2 :
4 \times 3 = 12
10 + 2 \times 3 + 12 = 28

Donc lʼaire de la figure est de 28 cm^2.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

45
Problème similaire
Triangles.

✔ Je structure mon raisonnement

Exprimez lʼaire de la partie verte, en fonction de d.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Mathématiques Cycle 4

Problèmes résolus

44 Calcul d'aire.

45 Problème similaireTriangles.

Une erreur sur la page ? Une idée à proposer ?

44
Calcul d'aire.

45
Problème similaire
Triangles.