Enseignement scientifique Terminale - 2024
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Sciences, climat et société
Ch. 1
L’atmosphère terrestre et la vie
Ch. 2
La complexité du système climatique
Ch. 3
Le climat du futur
Se préparer à l'évaluation - Thème 1
Le futur des énergies
Ch. 4
Deux siècles d’énergie électrique
Ch. 5
Conversion et transport de l’énergie électrique
Ch. 6
Énergie, développement et futur climatique
Se préparer à l'évaluation - Thème 2
Une histoire du vivant
Ch. 7
La biodiversité et son évolution
Ch. 8
L’évolution comme grille de lecture du monde
Ch. 9
L’évolution humaine
Ch. 10
Les modèles démographiques
Ch. 11
De l’informatique à l’intelligence artificielle
Se préparer à l'évaluation - Thème 3
Livret maths
Fiches méthode
Esprit critique et scientifique
Améliorer ses compétences
Fiches histoire
Annexes
Ch. 4
Activité 1 - documentaire
De l'induction à l'alternateur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Introduction
Une grande partie de la production mondiale d'électricité repose sur le phénomène d'induction électromagnétique mis en œuvre dans les alternateurs. Le barrage des Trois-Gorges en Chine est le barrage qui délivre la plus grande puissance électrique au monde grâce à cette technologie.
Problématique
Comment un alternateur génère-t-il de l'électricité ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Courant électrique
- Formes d'énergie
- Fréquence et période
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Documents
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Faraday et l'induction
Michael Faraday est un physicien qui a mis en évidence en
1831 le lien entre électricité, magnétisme et mouvement :
l'induction électromagnétique.
Ce phénomène apparaît lorsqu'un conducteur est en mouvement par rapport à un champ magnétique (produit par exemple par un aimant). Si cette variation est suffisamment importante, un courant électrique apparaît alors dans les conducteurs à proximité. On peut notamment l'observer en déplaçant un aimant à l'intérieur d'une bobine reliée à un dipôle électrique.
Ce phénomène apparaît lorsqu'un conducteur est en mouvement par rapport à un champ magnétique (produit par exemple par un aimant). Si cette variation est suffisamment importante, un courant électrique apparaît alors dans les conducteurs à proximité. On peut notamment l'observer en déplaçant un aimant à l'intérieur d'une bobine reliée à un dipôle électrique.

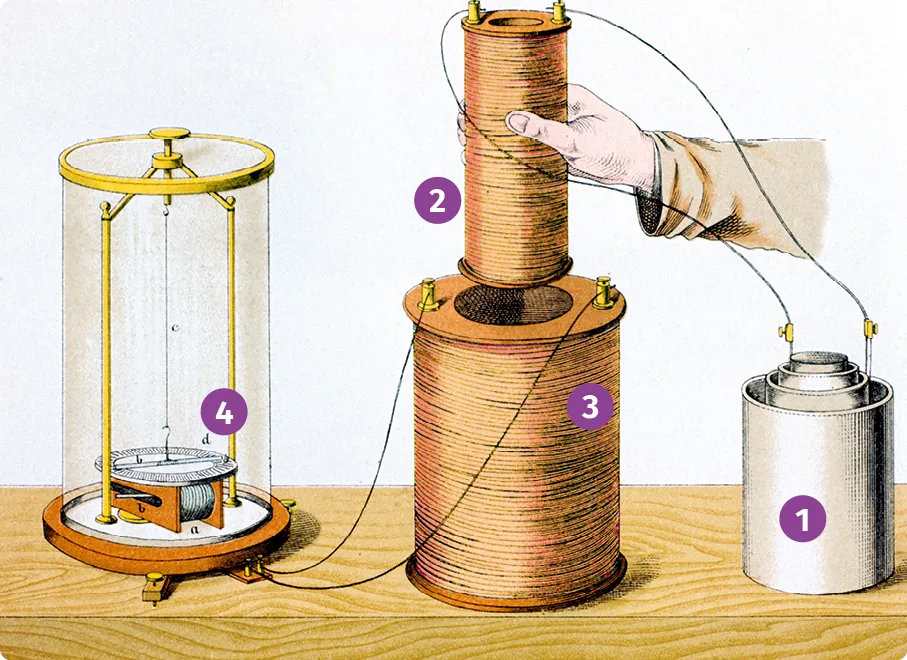
En revanche, si la bobine 2 était déplacée avec un mouvement périodique à l'intérieur de la bobine 3 , l'aiguille du galvanomètre 4 se mettait aussitôt à osciller, mettant en évidence qu'un courant électrique était apparu.
Ainsi, sans que les deux bobines ne soient en contact l'une et l'autre, le seul mouvement de la bobine 2 permettait d'induire un courant électrique alternatif dans la bobine 3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2 Fonctionnement d'un alternateur
Un alternateur est un dispositif de conversion d'énergie
reposant sur le phénomène d'induction électromagnétique.
Il est notamment utilisé dans les centrales pour produire de
l'électricité.
Pour cela, une turbine est mise en mouvement par l'écoulement d'un fluide, comme de la vapeur d'eau ou de l'eau liquide. Ce mouvement entraîne un rotor constitué d'aimants, ce qui génère un courant électrique par induction dans le stator, constitué d'un conducteur électrique. L'énergie mécanique du fluide est ainsi convertie en énergie électrique.
Pour cela, une turbine est mise en mouvement par l'écoulement d'un fluide, comme de la vapeur d'eau ou de l'eau liquide. Ce mouvement entraîne un rotor constitué d'aimants, ce qui génère un courant électrique par induction dans le stator, constitué d'un conducteur électrique. L'énergie mécanique du fluide est ainsi convertie en énergie électrique.
Schéma animé

Schéma statique

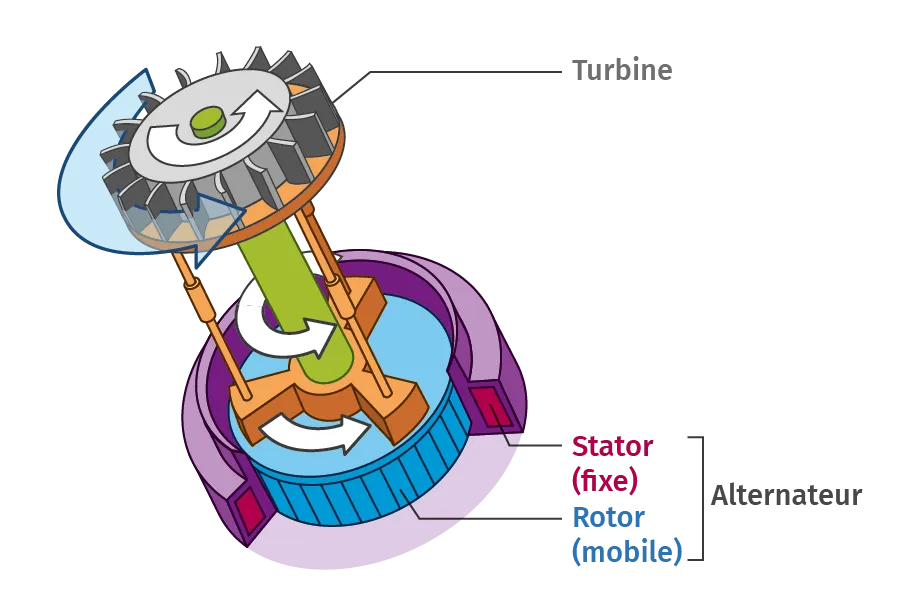
Schéma d'un alternateur couplé à une turbine
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rendez-vous pour simuler
le phénomène d'induction électromagnétique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3Rendement d'un alternateur
De manière générale, le rendement r d'un convertisseur est
le rapport entre la puissance utile Pu délivrée par celui-ci et
la puissance Pf qui lui est fournie. Dans le cas d'un alternateur, on a :
r=\frac{P_{\mathrm{u}}}{P_{\mathrm{f}}} \quad \left\lvert\, \begin{aligned}
& r: \text { rendement de conversion } \\
& P_{\mathrm{u}}: \text { puissance électrique induite dans le stator }(\mathrm{W}) \\
& P_{\mathrm{f}}: \text { puissance mécanique fournie à l'alternateur }(\mathrm{W})
\end{aligned}\right.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
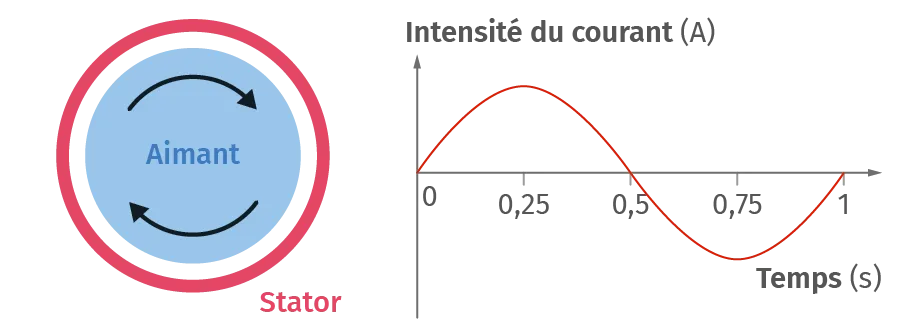
Doc. 4Obtention d'un courant
Lorsque le rotor est composé d'un seul aimant et qu'il fait
un tour en une seconde, le courant alternatif induit dans le
stator possède alors une fréquence de 1 Hz.

Lorsque le rotor est composé de deux aimants et qu'il fait un tour en une seconde, le courant induit dans le stator possède une fréquence de 2 Hz.

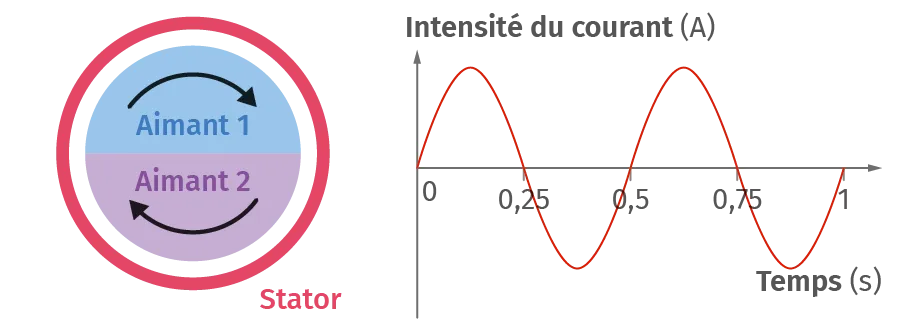


Lorsque le rotor est composé de deux aimants et qu'il fait un tour en une seconde, le courant induit dans le stator possède une fréquence de 2 Hz.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une animation pour visualiser l'effet du nombre d'aimants sur le courant.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 5Barrage des Trois-Gorges


Le barrage des Trois-Gorges en Chine est constitué de 34 alternateurs. Les rotors sont mis en mouvement par le passage de l'eau dans les turbines.
La puissance libérée par la chute de l'eau peut être estimée à l'aide de la relation :
P_{\text {chute }}=h \cdot D_\mathrm{~V} \cdot \rho \cdot g \left\lvert\, \begin{aligned}
& P_{\text {chute }} \text { : puissance mécanique associée } \\
& \text { à la chute de l'eau }(\mathrm{W}) \\
& h: \text { hauteur de la chute d'eau }(\mathrm{m}) \\
& D _\mathrm{~V}: \text { débit volumique }\left(\mathrm{m}^{3} \cdot \mathrm{s}^{-1}\right) \\
& \rho: \text { masse volumique de l'eau }\left(\mathrm{kg}^{-1} \cdot \mathrm{m}^{-3}\right) \\
& g: \text { intensité de pesanteur }\left(\mathrm{N} \cdot \mathrm{kg}^{-1}\right)
\end{aligned}\right.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Hauteur de chute : h = 80 m
- Puissance électrique délivrée par un alternateur du barrage des Trois-Gorges : Pu = 660 MW
- Rendement des alternateurs : r = 0,96
- Débit volumique de l'eau du barrage : DV = 34 000 m3·s-1
- Fréquence du courant électrique en Chine : f = 50 Hz
- Intensité de pesanteur : g = 9,81 N·kg-1
- Masse volumique de l'eau : \rho = 1,0 x 103 kg·m-3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Doc. 1 Identifier la condition à respecter pour qu'un champ magnétique puisse produire le phénomène d'induction électromagnétique.
2. Doc. 1 Préciser le type de courant électrique créé dans la bobine 3 lorsque l'on communique à l'aimant un mouvement de translation périodique comme dans l'expérience de Faraday.
3. Doc. 2 et Doc. 4 Qualifier le mouvement du rotor par rapport au stator permettant de produire le même type de courant électrique.
4. Doc. 5 Calculer la puissance Pchute résultant de la chute de l'eau au niveau du barrage des Trois-Gorges.
5. Doc. 3 Déterminer la puissance Pf fournie par la turbine à l'alternateur.
6. Doc. 5 Proposer une explication à la différence entre la puissance Pchute provenant de la chute de l'eau et la puissance Pf fournie par la turbine à l'alternateur.
7. Doc. 4 La fréquence f du courant induit est donnée par :
Sachant que la vitesse de rotation \omega des alternateurs
est de 0,8 tr·s-1, déduire les fréquences f possibles du courant électrique produit pour 20, 40, 80 et 100 aimants. Comparer ces fréquences à celle du courant du réseau électrique chinois.
f=N \cdot \omega \quad \left\lvert\, \begin{aligned}
& f: \text { fréquence du courant électrique } \\
& N: \text { nombre d'aimants du rotor } \\
& \omega: \text { vitesse de rotation du rotor }\left(\mathrm{tr} \cdot \mathrm{s}^{-1}\right)
\end{aligned}\right.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Courant électrique alternatif : courant électrique changeant de sens périodiquement.
Galvanomètre : appareil permettant de détecter et de mesurer le passage d'un courant électrique.
Induction électromagnétique : phénomène correspondant à l'apparition d'un courant électrique dans un conducteur en mouvement par rapport à un champ magnétique.
Galvanomètre : appareil permettant de détecter et de mesurer le passage d'un courant électrique.
Induction électromagnétique : phénomène correspondant à l'apparition d'un courant électrique dans un conducteur en mouvement par rapport à un champ magnétique.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
