Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 3
Applications
Suites numériques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer un terme de rang donné d'une suite géométrique définie par l'expression du terme de rang \bm{n}
1.
Identifier le premier terme et la raison q de la suite géométrique.
2. Déterminer le rang n du terme à calculer.
3. Calculer le terme de rang n donné :
- en appliquant la formule u_{n}=u_{0} \times q^{n} si le premier terme de la suite est u_0 ;
- en appliquant la formule u_{n}=u_{1} \times q^{n-1} si le premier terme de la suite est u_1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer le sens de variation d'une suite géométrique à l'aide de sa raison \bm{q \gt 0} et de son premier terme
Identifier le signe du premier terme de la suite géométrique ainsi que la valeur de sa raison q puis utiliser le tableau suivant.
| 0 \lt q \lt 1 | q=1 | q \gt 1 | |
|---|---|---|---|
| Premier terme \gt 0 | décroissante | constante | croissante |
| Premier terme \lt 0 | croissante | constante | décroissante |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer la somme des termes consécutifs d'une suite géométrique
1.
Identifier la valeur du premier terme et la raison q de la suite géométrique.
2. Déterminer le nombre de termes que l'on veut additionner.
3. Calculer la somme des termes consécutifs en appliquant la formule :
\mathrm{S}=\text { premier terme } \times \frac{1-q^{\text {nombre de termes }}}{1-q}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer un terme de rang donné d'une suite géométrique définie par récurrence
On considère la suite (u_n) définie par :
- son premier terme u_0 ou u_1 ;
- une relation de récurrence u_{n+1}=f\left(u_{n}\right) où f est une fonction.
1. Identifier la valeur du premier terme ainsi que la fonction f.
2. Appliquer la fonction sur la valeur du premier terme pour obtenir celle du deuxième terme.
3. Reproduire le point 2. jusqu'à obtenir la valeur du terme de rang voulu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Mise en pratique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCM
Une ou plusieurs bonnes réponses possibles.
1. Parmi les suites ci-dessus dont on donne les quatre premiers termes, déterminer celles pouvant être géométriques.
2. La suite géométrique (u_n) représentée graphiquement ci-dessous est :
Le zoom est accessible dans la version Premium.
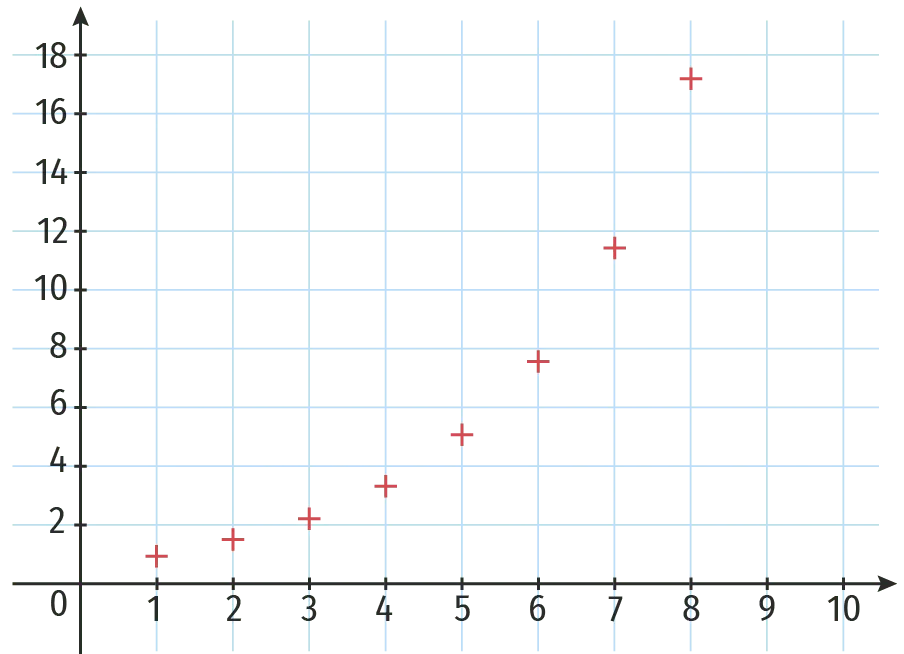
3. Les trois premiers termes d'une suite géométrique (u_n) définie par u_{1}=2 et q = 3 sont :
4. Soit (u_n) une suite géométrique définie par u_{0}=56 et de raison q = 0{,}2.
5. Soit (t_n) une suite géométrique de premier terme t_{1}=1{,}5 et de raison q = 2.
6. Soit (u_n) une suite géométrique de premier terme u_{1}=-10 et de deuxième terme u_{2}=-5.
La valeur de la raison de cette suite est :
4. Soit (u_n) une suite géométrique définie par u_{0}=56 et de raison q = 0{,}2.
5. Soit (t_n) une suite géométrique de premier terme t_{1}=1{,}5 et de raison q = 2.
6. Soit (u_n) une suite géométrique de premier terme u_{1}=-10 et de deuxième terme u_{2}=-5.
La valeur de la raison de cette suite est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème
Tom dépose 1 500 € sur un compte épargne pour pouvoir s'acheter une moto à 2 250 € dans neuf ans. Ce compte lui rapporte 4,5 % d'intérêts par an déposés directement sur le compte épargne.
On note u_n le montant disponible sur le compte la ne année.
On note u_n le montant disponible sur le compte la ne année.
Problématique
Tom pourra-t-il s'acheter la moto dans neuf ans ?
Le zoom est accessible dans la version Premium.
1.
Donner la valeur du premier terme u_1 et celle de la raison q.
2. Calculer, au centième près, les valeurs u_2 et u_3.
3. Exprimer u_n en fonction de n, pour tout entier naturel n non nul.
4. Calculer le montant disponible sur le compte la dixième année.
5. Répondre à la problématique.
2. Calculer, au centième près, les valeurs u_2 et u_3.
3. Exprimer u_n en fonction de n, pour tout entier naturel n non nul.
4. Calculer le montant disponible sur le compte la dixième année.
5. Répondre à la problématique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Réviser les notions de ce chapitre grâce à cette activité interactive.
Pour une utilisation optimale, réaliser l'activité en plein écran.
Genially
Pour une utilisation optimale, réaliser l'activité en plein écran.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah