Mathématiques 3e - 2021

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Annexes
Scratch
Dossier brevet
Rappels, Index, Compétences
Révisions Genially
Calcul littéral
Plan de travail
Chapitre 9
Outils numériques
Probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14[Rais.6]
Le but de ce jeu est de trouver, en un minimum de propositions, un nombre choisi au hasard par en suivant le procédé suivant.
- Scratch choisit un nombre aléatoire entre 1 et 100.
- Le joueur fait une première proposition.
- Scratch compare la proposition avec le nombre à trouver et indique si celui‑ci est inférieur ou supérieur à la proposition.
- Le joueur fait une seconde proposition et ainsi de suite.
- Quand le nombre est trouvé, le jeu s'arrête.
1. Écrire un algorithme répondant à ces critères.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15[Rais.6 - Ch.3]
Douze cafards fous organisent une course. Elle se déroule comme suit. Chaque cafard porte un numéro : tous sont différents et sont compris entre 1 et 12. Un parieur choisit un nombre au hasard compris entre 1 et 12. Le cafard qui porte le nombre choisi avance dʼun pas. Puis, le parieur recommence jusquʼà ce que lʼun des cafards passe la ligne dʼarrivée.


Retrouvez le fichier Scratch prêt à être complété.
1. a. Modifier le script afin que la course se déroule selon la règle établie par les cafards.
Le cafard qui porte comme numéro la somme des deux nombres choisis avance dʼun pas. Puis il recommence jusquʼà ce que lʼun des cafards passe la ligne dʼarrivée.
a.
Le cafard numéro 1 déclare forfait. Pourquoi ?
b.
Comment peut‑on désigner lʼévénement « Le cafard 1 gagne la course. » ?
c.
Modifier le script afin que la course se déroule selon la nouvelle règle.
d.
Les onze cafards restants ont‑ils la même chance de gagner ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16[Rep.8 - Rais.6]
Sur un tableur, la commande = ALEA.ENTRE.BORNES(1 ; n) permet de faire afficher un nombre entier aléatoire entre 1 et n. Cela permet de simuler une expérience à n issues : à chaque nombre entier correspond
une issue.
1.
Quelle formule peut‑on saisir pour simuler le lancer d'une pièce ?
2.
Quelle formule peut‑on saisir pour simuler le lancer d'un dé à six faces ?

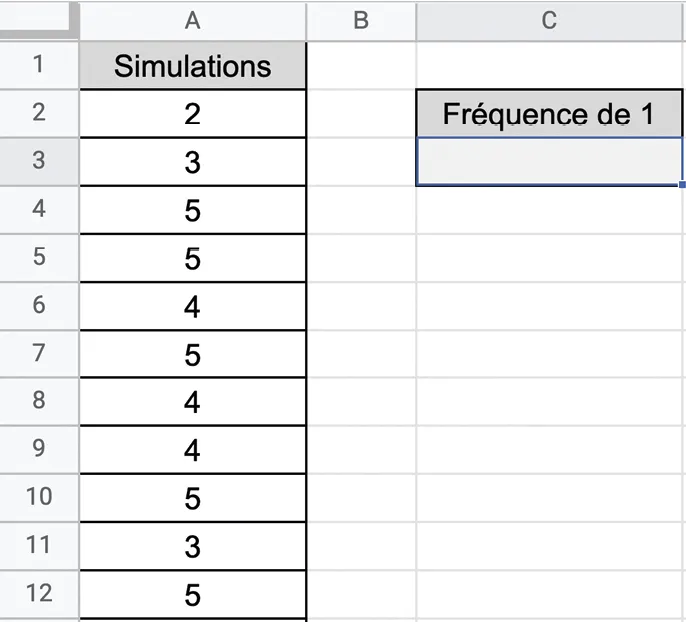
3. a.
Dans la feuille de calcul ci‑dessus, on a
utilisé la formule de la question 2. que l'on a
étirée de la cellule A2 à la cellule A31. À combien de lancers de dé cela correspond‑t‑il ?
b.
À l'aide de la commande = NB.SI(plage ; critère), donner la formule à saisir dans la cellule C3 pour déterminer la fréquence d'apparition du nombre 1 lors de tous ces lancers.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
