Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Annexes
Scratch
Dossier brevet
Rappels, Index, Compétences
Révisions Genially
Calcul littéral
Plan de travail
Chapitre 6
Exercices
Entraînement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Vérifier que les connaissances de base sont acquises.
Développer les connaissances.
Maîtriser les notions de manière approfondie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Fonctions linéaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
[Cal.4]
Déterminer le coefficient des fonctions linéaires dans chacun des cas suivants.
1. f(7)=63
2. g(-3)=51
2. g(-3)=51
3. h(5)=-11
4. k(-4{,}7)=-14{,}1
4. k(-4{,}7)=-14{,}1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
[Cal.4]
Déterminer le coefficient des fonctions linéaires dans chacun des cas suivants.
1. f\left(\frac{3}{4}\right)=1
2. g(2)=\frac{-7}{5}
2. g(2)=\frac{-7}{5}
3. 12,2 a pour antécédent 4 par h.
4. \frac{1}{3} a pour antécédent \frac{2}{9} par k.
4. \frac{1}{3} a pour antécédent \frac{2}{9} par k.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
[Cal.4 - Rais.5]
f est la fonction linéaire de coefficient -7. Dire si les affirmations suivantes sont vraies ou fausses. Justifier les réponses.
1. L'image de 3{,}4 par f est 23{,}8.
2. L'antécédent de -42 par f est 6.
2. L'antécédent de -42 par f est 6.
3. Le nombre x tel que f(x)=86{,}1 est -12{,}3.
4. f(\pi)=-21{,}98
4. f(\pi)=-21{,}98
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
Copie d'élève
[Rais.1 - Rais.5]
Le professeur de Pablo a demandé si le tableau de valeurs suivant peut être celui d'une fonction linéaire.
| \bm{x} | -5 | -3 | 1 | 2 | 7 |
| \bm{f(x)} | -7{,}5 | -4{,}5 | 1{,}5 | 3{,}5 | 10{,}5 |
Voici la réponse de Pablo.
f est linéaire si le tableau est un tableau de proportionnalité.
Comme -7{,}5 \div(-5)=1{,}5
-4{,}5 \div(-3)=1{,}5
1{,}5 \div 1 = 1{,}5 etc.
on a donc f(x)=1{,}5x.
f est une fonction linéaire.
Comme -7{,}5 \div(-5)=1{,}5
-4{,}5 \div(-3)=1{,}5
1{,}5 \div 1 = 1{,}5 etc.
on a donc f(x)=1{,}5x.
f est une fonction linéaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
[Rais.5 - Rep.3]
La droite (d) est la représentation graphique d'une fonction f.
Le zoom est accessible dans la version Premium.
1. Justifier l'affirmation : « La fonction f est une fonction linéaire. ».
2. a. Lire l'image de 4 par f.
b. Lire l'antécédent de 1 par f.
3. Donner l'expression de f(x).
b. Lire l'antécédent de 1 par f.
3. Donner l'expression de f(x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
[Rais.5 - Rep.3 - Cal.4]
La droite (d) est la représentation graphique d'une fonction f.
Le zoom est accessible dans la version Premium.
1. Quelle est la nature de la fonction f ? Justifier et donner son expression.
2. Déterminer par le calcul l'image de 5 par f.
3. Déterminer par le calcul l'antécédent de -4 par f.
3. Déterminer par le calcul l'antécédent de -4 par f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
[Rep.3]
Les droites (d_1), (d_2) et (d_3) représentent respectivement les fonctions f, g et h.Donner les expressions de f(x), g(x) et h(x).
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
[Rep.2 - Cal.4]
1. Dans un repère, tracer la courbe représentative de la fonction linéaire f: x \mapsto \frac{1}{4} x.
GeoGebra
2. Les points suivants appartiennent‑ils à cette courbe ? Justifier par le calcul.
a. \mathrm{A}(-8 \: ;-4)
b. \mathrm{B}(3 \: ; 1).
c. \mathrm{C}\left(\frac{4}{3} \: ; \frac{1}{3}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
[Rais.5 - Cal.2]
Les droites (d_1), (d_2), (d_3) et (d_4) représentent respectivement les fonctions f, g, h et k.
Le zoom est accessible dans la version Premium.
Les affirmations suivantes sont‑elles vraies ou fausses ? Justifier.
1. h(-3)=g(2)
2. f(2)\gt k(-1)
1. h(-3)=g(2)
2. f(2)\gt k(-1)
3. g(-4) \lt k(1)
4. f(1)=g(2)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
[Mod.3 - Rep.3 - Rep.2]
Le prix d'un litre d'essence est de 1,50 €.
1. On note f la fonction représentant le prix, en euro, de x litres d'essence. Quelle est la nature de cette fonction ? Justifier.
2.
1. On note f la fonction représentant le prix, en euro, de x litres d'essence. Quelle est la nature de cette fonction ? Justifier.
2.
a. Calculer f(5), f(25) et f(40).
b. Interpréter ces résultats dans le contexte de l'exercice.
3. a. Donner les coordonnées de trois points de la courbe représentative de la fonction f.
b. Dans un repère, tracer la courbe représentative de la fonction f.
4. Le prix d'un litre d'essence est passé à 1,30 €.
b. Dans un repère, tracer la courbe représentative de la fonction f.
GeoGebra
4. Le prix d'un litre d'essence est passé à 1,30 €.
a. Dans le même repère, représenter la courbe de la fonction g modélisant le nouveau prix.
b. Lire l'antécédent de 26 par g. Interpréter le résultat dans le contexte de l'exercice.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
[Ch.3 - Mod.8 - Rais.5 - Rep.2]
Voici trois programmes de calcul.
PROGRAMME A
\boxed{
\begin{array} { r|l }
1 & \text{Choisir un nombre} \\
2 & \text{Diviser par 10} \\
\end{array}
}
PROGRAMME B
\boxed{
\begin{array} { r|l }
1 & \text{Choisir un nombre} \\
2 & \text{Multiplier par 5} \\
3 & \text{Soustraire le nombre de départ} \\
\end{array}
}
PROGRAMME C
\boxed{
\begin{array} { r|l }
1 & \text{Choisir un nombre} \\
2 & \text{Ajouter 5} \\
3 & \text{Multiplier par 2} \\
4 & \text{Soustraire 10} \\
\end{array}
}
1. Pour un nombre x choisi, donner l'expression du nombre obtenu par chaque programme.
2. Abdel affirme : « Ces trois programmes correspondent à des fonctions linéaires. ». A‑t‑il raison ? Justifier.
3. Représenter ces trois fonctions dans un même repère.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
Inversé
[Ch.2 - Com.1]
On considère la fonction linéaire f: x \mapsto 3,5 x. Imaginer une situation de proportionnalité modélisée par cette fonction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
[Ch.2 - Mod.5 - Mod.3]
La vitesse moyenne d'un TER (Train express régional) est de 160 km/h. On désigne par f la fonction qui modélise la distance parcourue (en kilomètre) pour une durée t (en heure).
1. Quelle est la nature de cette fonction ? Donner son expression.
1. Quelle est la nature de cette fonction ? Donner son expression.
2. Calculer f(2) et f(0{,}5). Interpréter ces résultats.
3. Calculer l'antécédent de 200 par f. Interpréter ce résultat.
3. Calculer l'antécédent de 200 par f. Interpréter ce résultat.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Fonctions affines
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
[Rep.2 - Cal.4]
On considère la fonction affine définie par f(x)=-0{,}25 x+6.
1. Tracer la courbe représentative de la fonction f à l'aide de deux points.
1. Tracer la courbe représentative de la fonction f à l'aide de deux points.
GeoGebra
2. Lire l'antécédent de 7 par f.
3. Résoudre l'équation -0{,}25x + 6 = 7. Que remarque‑t‑on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
[Rep.2 - Cal.4]
1. Dans un repère, tracer la courbe représentative de la fonction affine f: x \mapsto 4 x-3.
2. Les points suivants appartiennent‑ils à cette courbe ? Justifier.
GeoGebra
2. Les points suivants appartiennent‑ils à cette courbe ? Justifier.
a. \mathrm{A}(5 \: ; 17)
b. \mathrm{B}(-2 \: ;-12)
b. \mathrm{B}(-2 \: ;-12)
c. \mathrm{C}\left(-\frac{1}{4} \: ;-2\right)
d. \mathrm{D}(0 \: ;-3)
d. \mathrm{D}(0 \: ;-3)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
[Rep.2 - Cal.4]
On considère les fonctions f: x \mapsto \frac{3}{5} x-5 et g: x \mapsto-x+3.
1. Dans un même repère, tracer :
a. la courbe représentative de f en calculant les coordonnées de deux points ;
b. la courbe représentative de g en s'aidant du coefficient directeur et de l'ordonnée à l'origine.
1. Dans un même repère, tracer :
a. la courbe représentative de f en calculant les coordonnées de deux points ;
GeoGebra
b. la courbe représentative de g en s'aidant du coefficient directeur et de l'ordonnée à l'origine.
2. a. Lire l'antécédent de -2 par f.
b. Lire l'antécédent de -2 par g.
b. Lire l'antécédent de -2 par g.
c. Que remarque‑t‑on ?
d. Retrouver ce résultat par le calcul.
d. Retrouver ce résultat par le calcul.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
Inversé
[Ch.2 - Com.1]
On considère la fonction affine f: x \mapsto 12 x + 40.
Imaginer une situation qui peut être modélisée par cette fonction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
[Cal.2]
Les droites (d_1), (d_2), (d_3) et (d_4) représentent des fonctions affines.
Le zoom est accessible dans la version Premium.
D'après l'allure des courbes représentatives, compléter le tableau en précisant le signe du coefficient directeur a et le signe de l'ordonnée à l'origine b.
| \bm{(d_1)} | \bm{(d_2)} | \bm{(d_3)} | \bm{(d_4)} | |
|---|---|---|---|---|
| Signe de \bm{a} | ||||
| Signe de \bm{b} |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
[Cal.2 - Cal.3]
Les droites (d_1), (d_2), (d_3), (d_4), (d_5) et (d_6) représentent des fonctions affines.
Le zoom est accessible dans la version Premium.
Citer la droite ayant :
1. le plus petit coefficient directeur ;
2. le plus grand coefficient directeur ;
1. le plus petit coefficient directeur ;
2. le plus grand coefficient directeur ;
3. le plus grand coefficient directeur strictement négatif ;
4. la plus petite ordonnée à l'origine ;
5. un coefficient directeur nul.
4. la plus petite ordonnée à l'origine ;
5. un coefficient directeur nul.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
[Mod.9 - Cal.4]
Dans une salle de sport, les frais d'inscription sont de 49 € et l'abonnement coûte 29,95 € par mois.
Julien décide de s'inscrire.
1. Combien paiera‑t‑il pour une durée de quatre mois ? Pour une durée d'un an ?
Julien décide de s'inscrire.
1. Combien paiera‑t‑il pour une durée de quatre mois ? Pour une durée d'un an ?
2. On note f la fonction qui modélise le prix à payer, en euro, pour x mois d'abonnement.
a. Donner l'expression de f(x).
b. Julien a payé 258,65 €. Quelle était la durée de son abonnement ?
a. Donner l'expression de f(x).
b. Julien a payé 258,65 €. Quelle était la durée de son abonnement ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
[Mod.9 - Cal.4]
Le zoom est accessible dans la version Premium.
Selon le modèle ISA (International Standard Atmosphere), l'atmosphère est divisée en différentes couches avec une distribution linéaire de la température.
Ainsi entre 0 et 11 km, le modèle définit une température de 15 °C au niveau de la mer et une baisse de 6,5 °C par kilomètre.
Ainsi entre 0 et 11 km, le modèle définit une température de 15 °C au niveau de la mer et une baisse de 6,5 °C par kilomètre.
1. On considère la fonction f qui modélise la température (en °C) en fonction de l'altitude x (en km). Donner l'expression de f(x) en fonction de x.
2. a. Calculer f(5) et interpréter le résultat.
b. Déterminer l'antécédent de -30,5 par f et interpréter le résultat.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
Démo
[Rais.3 - Ch.2]
On souhaite démontrer la propriété : « Si f est une fonction affine définie par {f(x)=a x+b} et si x_1 et x_2 sont deux nombres distincts, alors {a=\frac{f\left(x_{2}\right)-f\left(x_{1}\right)}{x_{2}-x_{1}}}. »
1. Donner l'expression def(x_1) et f(x_2).
1. Donner l'expression def(x_1) et f(x_2).
2. a. Démontrer que f\left(x_{2}\right)-f\left(x_{1}\right)=a x_{2}-a x_{1}.
b. Factoriser le second membre de l'égalité.
c. En déduire que a=\frac{f\left(x_{2}\right)-f\left(x_{1}\right)}{x_{2}-x_{1}} avec x_{1} \neq x_{2}.
b. Factoriser le second membre de l'égalité.
c. En déduire que a=\frac{f\left(x_{2}\right)-f\left(x_{1}\right)}{x_{2}-x_{1}} avec x_{1} \neq x_{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
Copie d'élève
[Ch.2 - Rais.5 - Com.4]
Soit (d) la droite de coefficient directeur a représentant la fonction affine f.
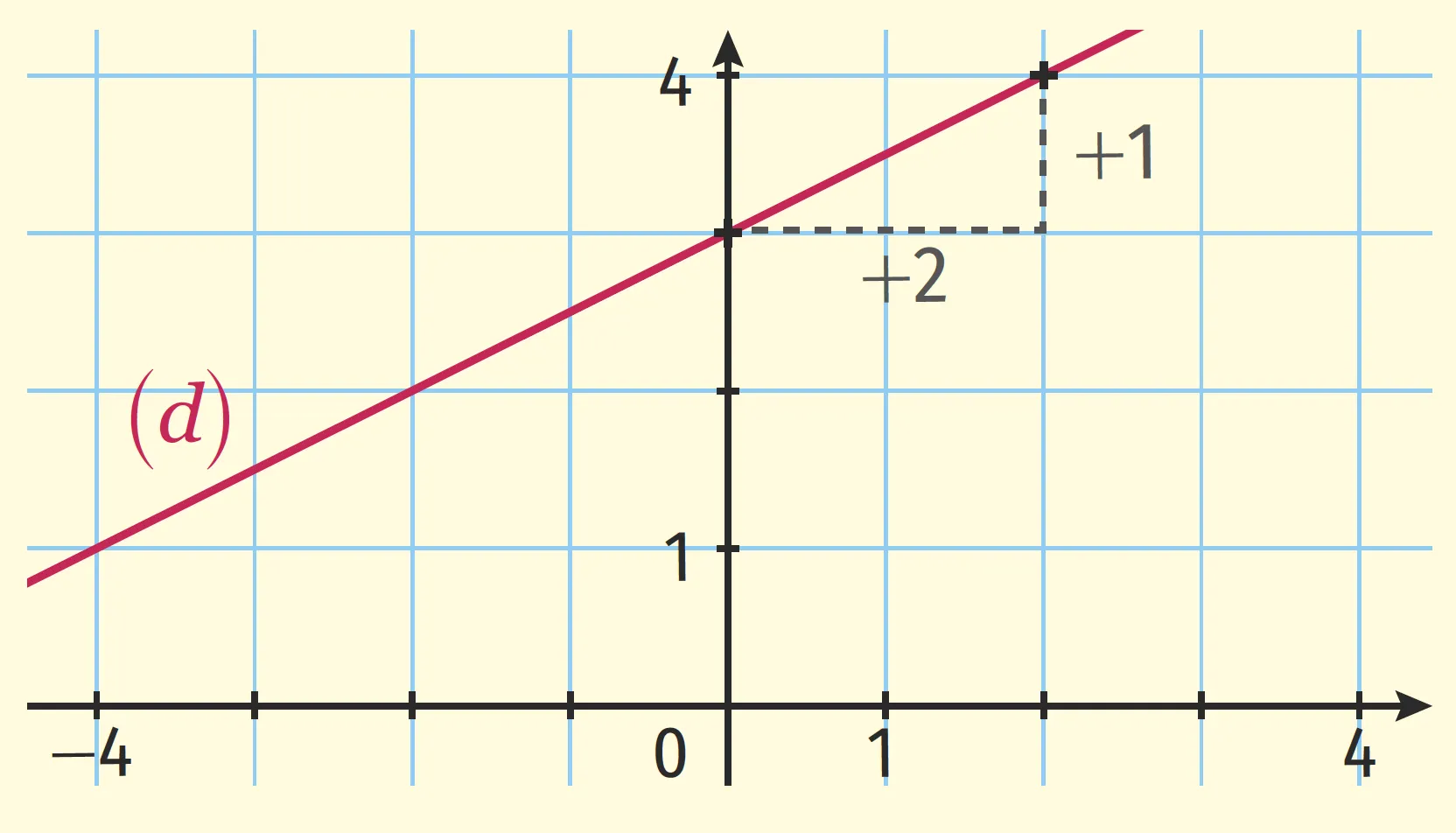
Le professeur de Clara a demandé de compléter, pour chaque graphique, la phrase : « Quand x augmente de ... alors f(x) ... de ... . Ainsi a = ... et a est ... . ».
Voici sa réponse.
Indiquer les erreurs commises par Clara puis proposer une correction.
Le professeur de Clara a demandé de compléter, pour chaque graphique, la phrase : « Quand x augmente de ... alors f(x) ... de ... . Ainsi a = ... et a est ... . ».
Voici sa réponse.
1. Quand x augmente de 2, alors f(x) augmente de 1. Ainsi a=1 et a est positif.
Le zoom est accessible dans la version Premium.
2. Quand x augmente de 1, alors f(x) diminue de 2. Ainsi a=2 et a est positif.
Le zoom est accessible dans la version Premium.
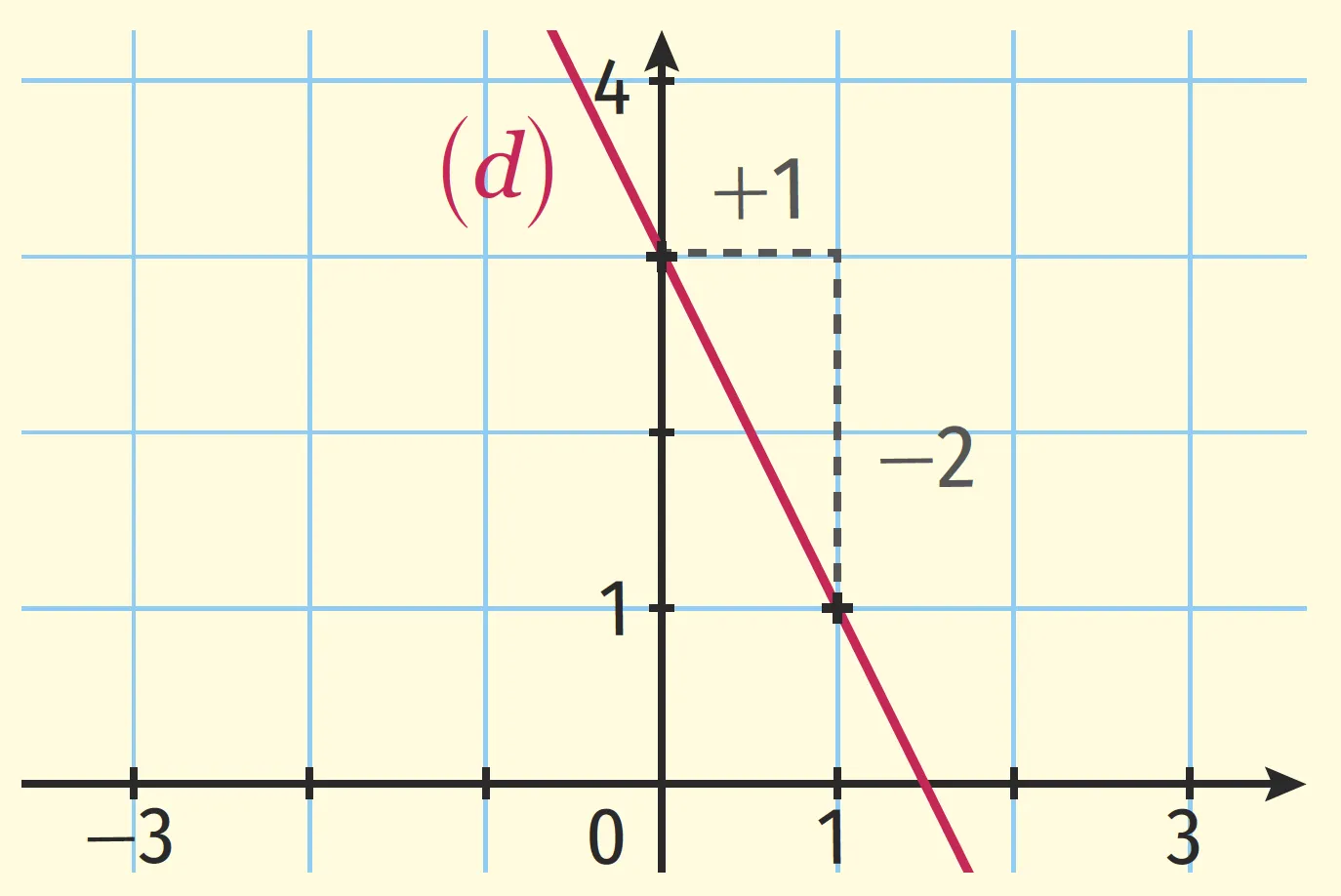
Indiquer les erreurs commises par Clara puis proposer une correction.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah