Mathématiques Terminale Bac Pro - Cahier

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 4
Activité B
Un peu de plomberie
Capacités : Déterminer la dérivée d'une fonction polynôme de degré inférieur ou égal à 3.
Dresser son tableau de variations et l᾽exploiter.
Déterminer ses éventuels extremums locaux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
M. Dupont fait des travaux dans sa cuisine et il souhaite déplacer son évier. La pose d'un évier de cuisine doit respecter les normes suivantes :
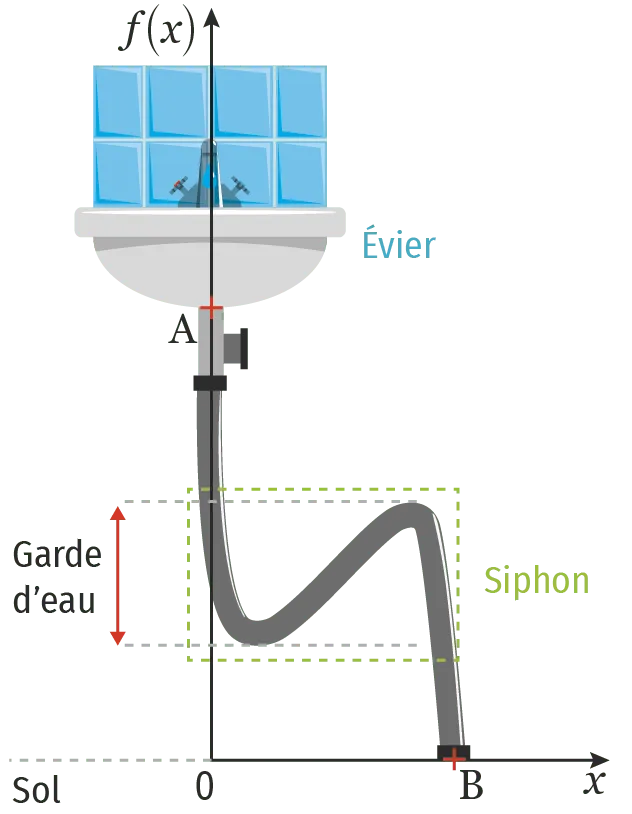
Un siphon est un dispositif de tuyauterie en forme de « S » incurvé et rempli d'eau propre utilisé dans les canalisations (un évier par exemple) pour empêcher les mauvaises odeurs de remonter et de se diffuser vers le ou les orifice(s) d᾽évacuation. La garde d'eau est la hauteur d'eau propre continuellement présente dans le siphon.
La forme du tuyau d'évacuation d'ea est modélisée par la fonction f définie sur [\:0 ; 8\:] par f(x)=-x^{3}+13,5 x^{2}-54 x+83 où x représente la distance, en centimètre, au sol et f(x) la hauteur, en centimètre, du tuyau.
- la hauteur de l'évier par rapport au sol doit être de 83 cm ;
- la garde d'eau doit être supérieure à 5 cm.
Un siphon est un dispositif de tuyauterie en forme de « S » incurvé et rempli d'eau propre utilisé dans les canalisations (un évier par exemple) pour empêcher les mauvaises odeurs de remonter et de se diffuser vers le ou les orifice(s) d᾽évacuation. La garde d'eau est la hauteur d'eau propre continuellement présente dans le siphon.
La forme du tuyau d'évacuation d'ea est modélisée par la fonction f définie sur [\:0 ; 8\:] par f(x)=-x^{3}+13,5 x^{2}-54 x+83 où x représente la distance, en centimètre, au sol et f(x) la hauteur, en centimètre, du tuyau.
Problématique
Problématique : Les normes ont-elles été respectées ?

Aide
L᾽origine du repère se situe au sol, sous l᾽évier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie A
Contrainte sur la hauteur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1S'approprier
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Valider
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie B
Contrainte sur le siphon
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Réaliser
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Valider
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Réaliser
Dresser le tableau de signe de f^{\prime}(x) sur l'intervalle [0\:; 8].
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Réaliser
Dresser le tableau de variations de la fonction f sur l'intervalle [0\:; 8].
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Valider
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Communiquer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une fonction polynôme de degré 3 est une fonction f définie sur pour laquelle il existe quatre nombres réels a, b, c et d, avec a non nul, tels que, pour tout réel x, f(x)=a x^{3}+b x^{2}+c x+d.
Sa fonction dérivée f' est définie sur \Reals par f^{\prime}(x)=.
Sa fonction dérivée f' est définie sur \Reals par f^{\prime}(x)=
Pour s᾽entraîner :
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
