Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d’équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Chapitre 2
Bilan
Puissances
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44QCM[Cal.1 - Com.1 - Cal.4]
Cocher la (ou les) bonne(s) réponse(s).
1. Le produit de 15 facteurs tous égaux à -4 se note :
2. 10^{4}+10^{2}=
3. La notation scientifique de 0,002~54 est :
4. Le préfixe associé à 10^{6} est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45[Com.1]
Cet exercice est un « mots mêlés ». Compléter les cases par le mot correspondant à l'aide des indices donnés.
| 1 | ||||||||||
| 2 | ||||||||||
| 3 | ||||||||||
| 4 | 5 | |||||||||
| 6 | ||||||||||
| 7 | ||||||||||
| 8 | 9 | |||||||||
| 10 | ||||||||||
1. Préfixe associé à 0,000~001.
2. Préfixe associé à 10^{1} \times 10^{2}.
3. Nom de n dans l'écriture a^{n}.
4. Élément qui constitue un produit.
5. Préfixe associé à 10^{-3}.
2. Préfixe associé à 10^{1} \times 10^{2}.
3. Nom de n dans l'écriture a^{n}.
4. Élément qui constitue un produit.
5. Préfixe associé à 10^{-3}.
6. Résultat d'une multiplication.
7. 1000 \mathrm{~kg}=1 \ldots \ldots.
8. Préfixe associé à 10^{6} .
9. Préfixe associé à 1~000~000~000.
10. Préfixe associé à \frac{10^{-3}}{10^{6}}.
7. 1000 \mathrm{~kg}=1 \ldots \ldots.
8. Préfixe associé à 10^{6} .
9. Préfixe associé à 1~000~000~000.
10. Préfixe associé à \frac{10^{-3}}{10^{6}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46[Cal.4]
Donner l'écriture décimale des nombres suivants.
1. 2^{3}+10^{3}=
2. 7^{2}-(-2)^{4}=
3. (5,3-3,8)^{2}=
4. 4^{3} \div(-2)^{4}=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47[Cal.3]
Donner l'écriture décimale des nombres suivants.
1. 10^{3} \times 10^{2}=
2. 10^{3} \div 10^{7}=
3. \left(10^{3}\right)^{2}=
4. 10^{3}+10^{2}=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48[Cal.5 - Ch.1 - Mod.1]
Amélie lance une chaîne de tweets un lundi à 8 h. Chaque personne qui reçoit ce tweet doit l'envoyer à son tour à quatre personnes l'heure suivante, et ainsi de suite. On suppose qu'une personne ne le reçoit qu'une et une seule fois et que chaque personne ayant reçu le tweet poursuit la chaîne.
1. Combien de personnes ont reçu le tweet lundi à midi ?
2. Combien de personnes ont reçu le tweet lundi à 20 h ?
3. À partir de quelle heure peut-on supposer qu'au moins un milliard de personnes ont reçu le tweet d'Amélie ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49[Cal.5 - Rais.6 - Mod.10]
On introduit une population de lapins dans un milieu dans lequel ils n'ont pas de prédateurs. Ils peuvent ainsi proliférer sans que leur progression ne soit freinée. On écrit le suivant.
Le zoom est accessible dans la version Premium.
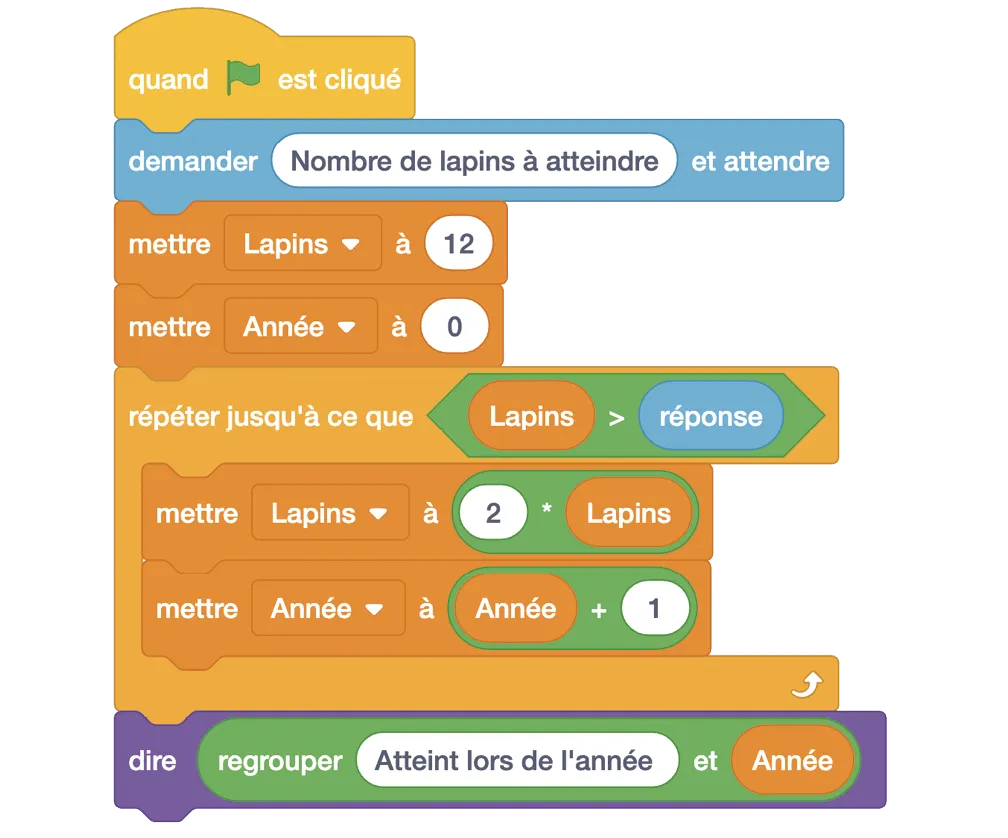
À l'aide de ce programme, déterminer les informations suivantes.
1. Le nombre initial de lapins :
2. La vitesse d'évolution de la population de lapins :
3. Le but de ce programme :
4. Le nombre de lapins au bout de 14 années :
1. Le nombre initial de lapins :
2. La vitesse d'évolution de la population de lapins :
3. Le but de ce programme :
4. Le nombre de lapins au bout de 14 années :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50[Cal.4 - Cal.1]
On considère les nombres \mathrm{A}=1,5 \times 10^{-3} et
\mathrm{B}=8,4 \times 10^{7}.
1. Donner l'écriture décimale de :
a. \text{A}+\text{B}=
b. \text{A} \times \text{B}=
b. \text{A} \times \text{B}=
2. Donner les notations scientifiques des résultats précédents.
a. \text{A}+\text{B}=
b. \text{A} \times \text{B}=
b. \text{A} \times \text{B}=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51[Mod.2 - Mod.1 - Cal.5 - Rais.5]
La force d'attraction gravitationnelle entre deux masses Masse 1 et Masse 2, en kg, est donnée, en newton (N), par la formule :\mathrm{F}=\frac{\mathrm{G} \times \text { Masse } 1 \times \text { Masse } 2}{\text { Distance }^{2}}
où Distance représente la distance entre les deux objets, en mètre, et \text{G} représente la constante gravitationnelle avec \mathrm{G}~\approx~6,67~\times~10^{-11}~\mathrm{~N}~\cdot~\mathrm{m}^{2} /~\mathrm{kg}^{2}.
On donne de plus les informations suivantes.
| Masse Soleil | Masse Terre | Masse Lune |
|---|---|---|
| 1,989 \times 10^{30} \mathrm{~kg} | 5,972 \times 10^{24} \mathrm{~kg} | 7,342 \times 10^{22} \mathrm{~kg} |
| Distance Soleil‑Terre | Distance Terre‑Lune |
|---|---|
| 149~500~000~000 \mathrm{~m} | 384~000~\mathrm{~km} |
1. Montrer que la force d'attraction gravitationnelle entre le Soleil et la Terre est d'environ 3,54 \times 10^{22} \mathrm{~N}.
2. Calculer la force d'attraction gravitationnelle entre la Terre et la Lune.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52[Cal.2 - Com.2]
On donne de plus les informations suivantes.
| Masse Uranus | Masse Mercure | Masse Saturne |
|---|---|---|
| 8,681 \times 10^{25} \mathrm{~kg} | 3,285 \times 10^{26} \mathrm{~g} | 5,683 \times 10^{20} \mathrm{~Gg} |
Comparer les masses d'Uranus, de Mercure et de Saturne.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Genially
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah