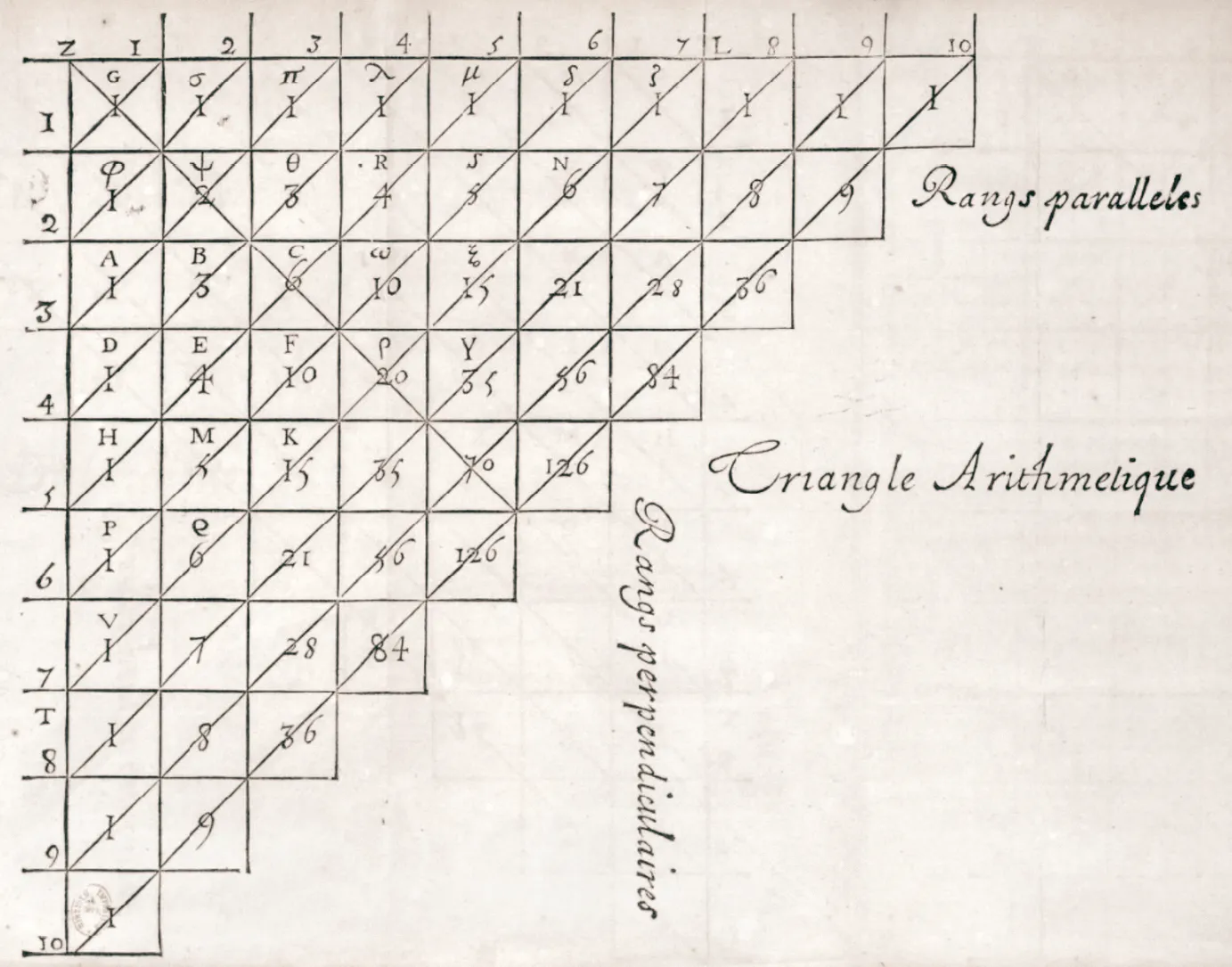
Le triangle de Pascal (1623-1662) est un tableau de nombres qui permet de déterminer, par une relation de récurrence, les coefficients binomiaux \left(\begin{array}{l} n \\ k \end{array}\right).
Le triangle est connu des mathématiciens bien avant Pascal (Perse au X^e siècle, Chine au XII^e siècle, etc.) mais Pascal est le premier à proposer, dans son Traité du triangle arithmétique publié en 1654, un ensemble de résultats le concernant. Pour les démontrer, il s'appuie sur le principe de raisonnement par récurrence.
On rappelle que l'on écrit de nos jours : \left(\begin{array}{l} n \\ k \end{array}\right)=\left(\begin{array}{l} n-1 \\ k-1 \end{array}\right)+\left(\begin{array}{c} n-1 \\ k \end{array}\right).

1

Quels sont les coefficients binomiaux présentés dans les cellules C et F du triangle de Pascal ?

Le programme ci-dessous rédigé en Python permet d'afficher le triangle de Pascal pour un nombre n de lignes demandé.

n = int(input("Nombre de rangs ?"))
l = []

for i in range(n) :
   l.append(1)
 print(l)
 
for k in range(2, n+1) :
   for i in range(1,n+1-k):
      l[i] = l[i-1]+l[i]
    del l[n+1 - k]
    print(l)

À quoi correspondent les variables n et k dans le tableau ?

3

Tester le programme pour différentes valeurs de n.
Comment retrouve-t-on le triangle donné en exemple par Pascal ?

4

Que permet d'afficher le code entre les lignes 4 et 6 ?

5

Examiner les lignes 8 à 12 : que représentent les indices \text{i} et k par comparaison avec le tableau de Pascal ?

6

À partir de cet algorithme, en construire un autre permettant de calculer \left(\begin{array}{l} n \\ k \end{array}\right).

Remarque

Python permet de travailler directement avec des variables de type matrice. Un autre algorithme les utilisant est présenté dans le

TP 2 du chapitre 1 page 43

.

En 1765, Euler établit un résultat de géométrie à propos de l'alignement du centre de gravité, de l'orthocentre et du centre circonscrit d'un triangle. Pour arriver à ses fins, Euler utilise des calculs de coordonnées. Sa démonstration tient sur vingt pages et est publiée dans un ouvrage du nom de Solution Facile à Certains Problèmes Très Difficiles ! La notion de vecteur n'existait pas...
Hermann Grassmann publie en 1844 son Die Lineale Ausdehnungslehre. Même si, sur le moment, cet ouvrage ne reçoit pas beaucoup d'échos, il a le mérite de proposer, pour la première fois, un algèbre d'ordre nouveau basé sur les vecteurs. Ce sera la naissance des espaces vectoriels. Les vecteurs existent de façon autonome et leurs résultats peuvent être appliqués à de nombreuses théories mathématiques, allant de la géométrie à l'informatique en passant par les polynômes. Malgré l'apparition d'une géométrie sans figure, de nombreuses démonstrations tiennent maintenant en quelques lignes.