3. Cercles et disques

a. Prendre plusieurs objets ayant une forme de tube (tube de colle, rouleau de scotch de déménagement, bouteille, etc.).
b. Poser chaque objet sur sa partie « ronde » et mesurer son diamètre. Mesurer ensuite son périmètre à l'aide d'une cordelette et d'une règle.
c. Peut-on prévoir le périmètre d'un disque de 10 cm de rayon ?

Le périmètre d'un cercle est proportionnel à son diamètre. Ainsi, si l'on multiplie par deux le diamètre, on multiplie par deux le périmètre.

Exemple : Le cercle noir a un diamètre quatre fois supérieur à celui du cercle violet. Son périmètre (« déroulé » en dessous) est aussi quatre fois supérieur à celui du cercle violet.

• La calculatrice en donne une valeur approchée plus précise grâce à la touche π !
 

Si un cercle a un diamètre de longueur D, alors il a un périmètre P de longueur \pi \times D. On a la formule :

• Périmètre = \pi \times  diamètre 
• P = \pi \times  D

Exemple : Un cercle de diamètre 2 cm a un périmètre mesurant 2 \times \pi cm. Une valeur approchée de \pi est 3,14. Son périmètre a donc une valeur approchée de 2 \times 3,14 cm = 6,28 cm.

On mesure souvent le rayon d'un cercle au lieu de son diamètre. Le diamètre est le double du rayon. Si un cercle a un rayon R, un diamètre D et  un périmètre P, on a donc les formules :

• Diamètre = 2 \times rayon 
• D = 2 \times R
• Périmètre = 2 \times \pi \times rayon 
• P = 2 \times \pi \times R

 Remarque : 
La formule P = \pi \times D donne une valeur exacte du périmètre. Ainsi un cercle de diamètre 7 cm a un périmètre mesurant exactement 7 \times \pi cm.

Exemple : Un cercle de rayon 3 cm a un périmètre mesurant exactement 2 \times 3 \times \pi cm = 6 \times \pi cm \approx 18\text{,}84 cm.

Mesurer le rayon et le diamètre du cercle. En déduire de deux manières différentes le périmètre de ce cercle.

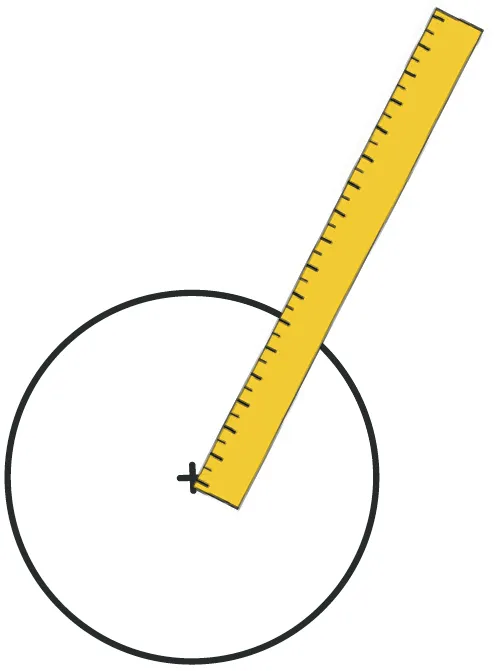
• Le rayon mesure 1 cm.
• Donc le périmètre mesure environ 2 \times 3,14 \times 1 cm = 6,28 \times 1 cm = 6,28 cm.
  • Le diamètre mesure 2 cm.
• Donc le périmètre mesure \pi \times 2 cm \approx 6,28 cm.

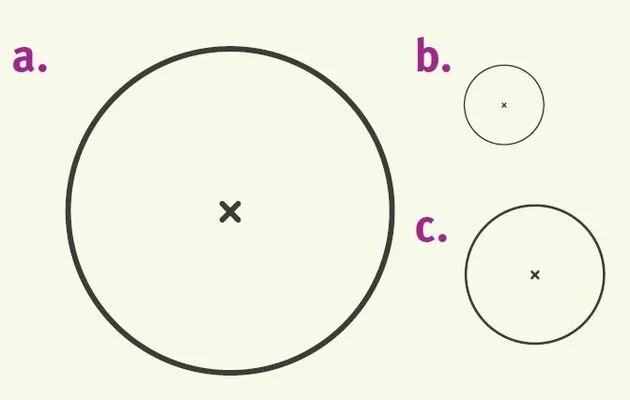
Donner une valeur approchée du périmètre.

a. Tracer un cercle de 8 cm de rayon.
b. Essayer de placer à l'intérieur de ce cercle deux cercles de 4 cm de rayon chacun, qui ne se chevauchent pas. Est-ce possible ?
c. L'aire d'un cercle est-elle donc proportionnelle au rayon du cercle ?


Ce disque fait 1 cm de rayon et les carreaux 1 mm de côté.

d. Ce disque fait 1 cm de rayon et les carreaux 1 mm de côté. Compter le nombre de carreaux qui sont entièrement dans le cercle, ainsi que le nombre de carreaux qui permet de recouvrir entièrement le cercle et son intérieur.
e. En déduire un encadrement de l'aire contenue dans le cercle, exprimé en cm^2.

• Un disque représente la surface qui est à l'intérieur d'un cercle.
  
  
  

  
  

  

  
  
• Pour obtenir l'aire d'un disque on multiplie son rayon par lui-même, puis par π.
• Si le rayon est noté R et l'aire A, on a la formule :
  • A = \pi \times R \times R
  • Aire = \pi \times rayon \times rayon

Exemple : L'aire d'un disque de rayon 3 cm vaut environ 3,14 \times 3 cm \times 3 cm = 3,14 \times 3 \times 3 cm^2 = 28,26 cm^2.

 Remarque : 
La formule A = \pi \times R \times R permet de donner une valeur exacte de l'aire. Ainsi, un cercle de rayon 4 cm a une aire mesurant exactement 16 \pi \times cm^2.

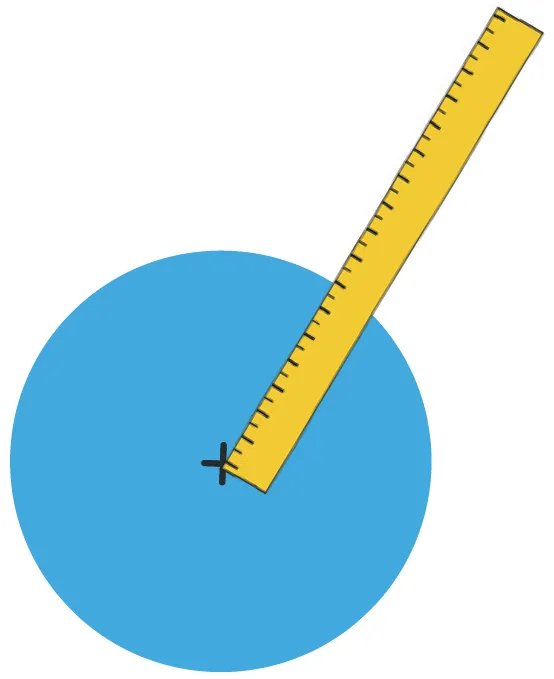
Donner une valeur approchée de l'aire de chaque disque.