Mathématiques 6e
Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Mes Pages
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 12
Exercices
Aire et périmètre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Échauffement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
Effectuer les changements d'unités.
1. 354 cm = m
2. 56 mm = cm
3. 9,41 hm = dam
4. 45,4 cm = m
5. 4,23 dm = hm
6. 477,53 m = km
1. 354 cm =
2. 56 mm =
3. 9,41 hm =
4. 45,4 cm =
5. 4,23 dm =
6. 477,53 m =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
Effectuer les changements d'unités.
1. 24,32 cm^2 = mm^2
2. 545,3 km^2 = hm^2
3. 441,74 m^2 = hm^2
4. 64 123 mm^2 = dm^2
5. 15 km^2 = m^2
1. 24,32 cm^2 =
2. 545,3 km^2 =
3. 441,74 m^2 =
4. 64 123 mm^2 =
5. 15 km^2 =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19


1. Comparer les périmètres des polygones de la figure a. sans les mesurer.

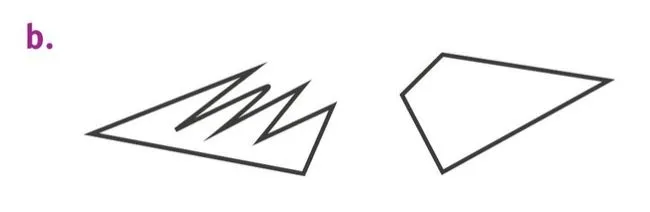
2. Comparer les périmètres des polygones de la figure b. sans les mesurer.

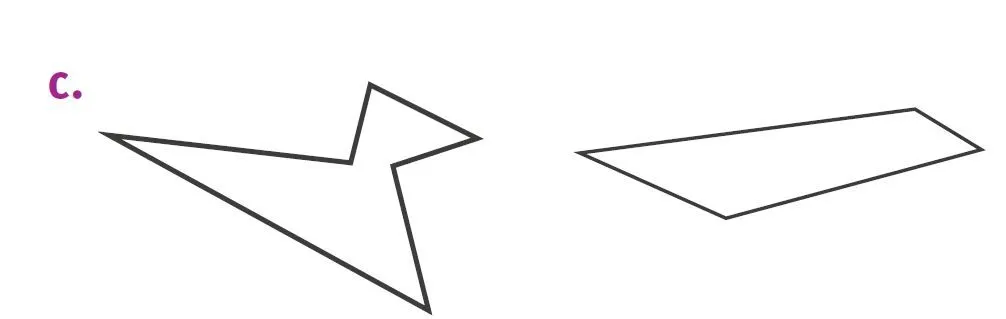
3. Comparer les périmètres des polygones de la figure c. sans les mesurer.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
Donner les périmètres.

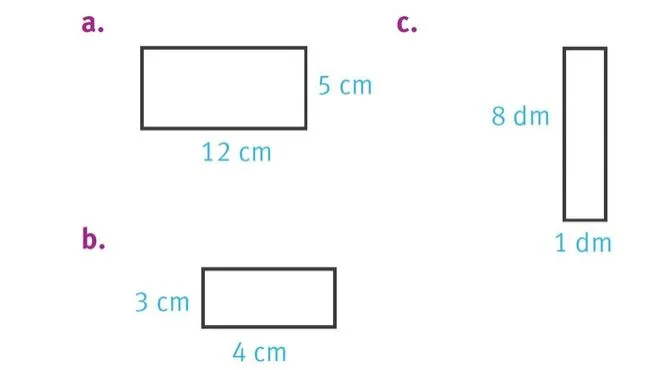
1. Du rectangle a.
2. Du rectangle b.
3. Du rectangle c.


1. Du rectangle a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
Donner le périmètre sans le mesurer.

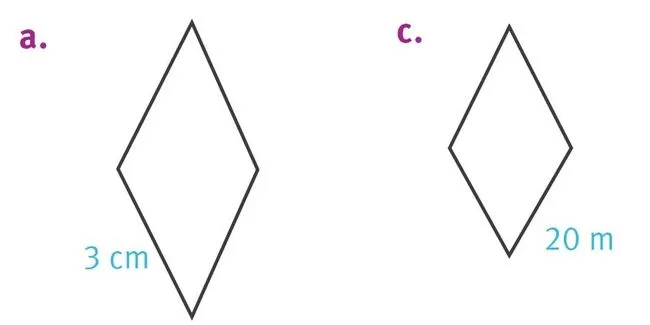

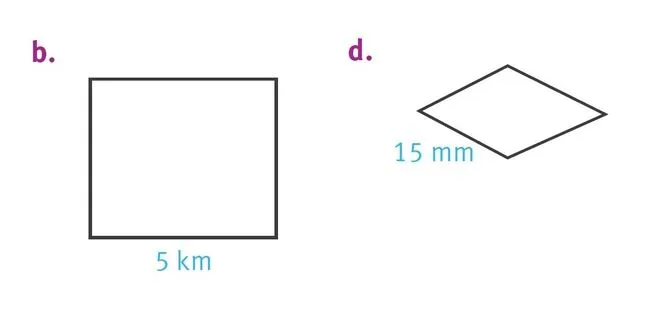
1. Du losange a.
2. Du rectangle b.
3. Du losange c.
4. Du losange d.




1. Du losange a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
Donner l'aire.

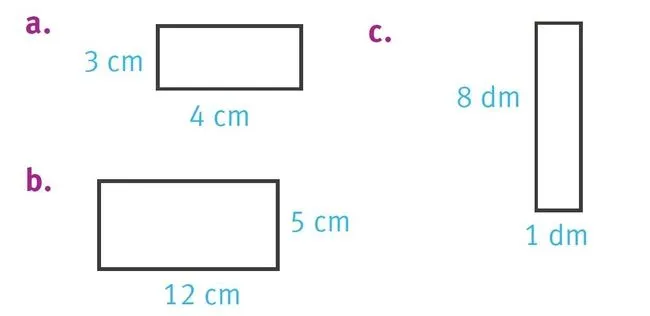
1. Du rectangle a.
2. Du rectangle b.
3. Du rectangle c.


1. Du rectangle a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Recopier chaque figure en s'aidant du quadrillage.

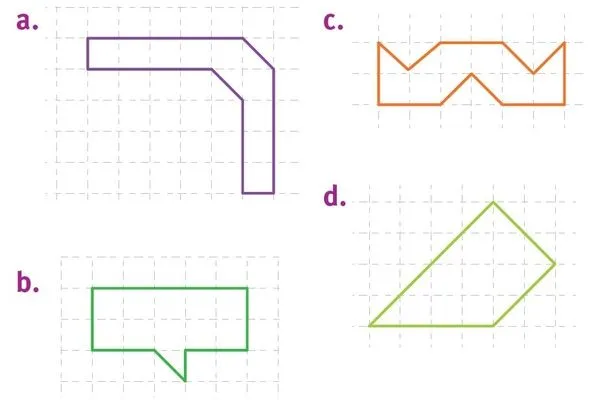


On prendra comme unité l'aire d'un demi carreau.
1. Donner l'aire de la figure a.
2. Donner l'aire de la figure b.
3. Donner l'aire de la figure c.
4. Donner l'aire de la figure d.
1. Donner l'aire de la figure a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Donner une valeur exacte du périmètre.

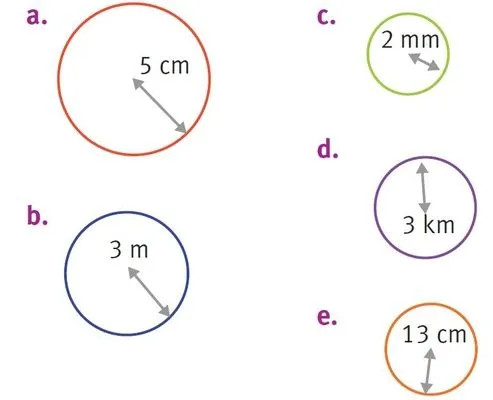
1. Du cercle a.
2. Du cercle b.
3. Du cercle c.
4. Du cercle d.
5. Du cercle e.


1. Du cercle a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Donner une valeur approchée du périmètre.


1. Du cercle a.
2. Du cercle b.
3. Du cercle c.
4. Du cercle d.
5. Du cercle e.


1. Du cercle a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Donner une valeur exacte de l'aire.


1. Du disque a.
2. Du disque b.
3. Du disque c.
4. Du disque d.
5. Du disque e.


1. Du disque a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Donner une valeur approchée de l'aire.


1. Du disque a.
2. Du disque b.
3. Du disque c.
4. Du disque d.
5. Du disque e.


1. Du disque a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
Donner les aires des triangles rectangles suivants.

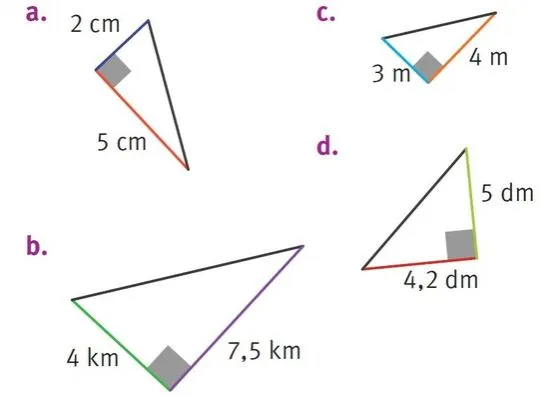
1. Y en a-t-il qui sont égales ?


1. Y en a-t-il qui sont égales ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Entraînement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
Pour chaque figure, mesurer son aire et son périmètre en s'aidant du quadrillage. On prendra comme unité de longueur le côté d'un carreau, et comme unité d'aire un carreau.

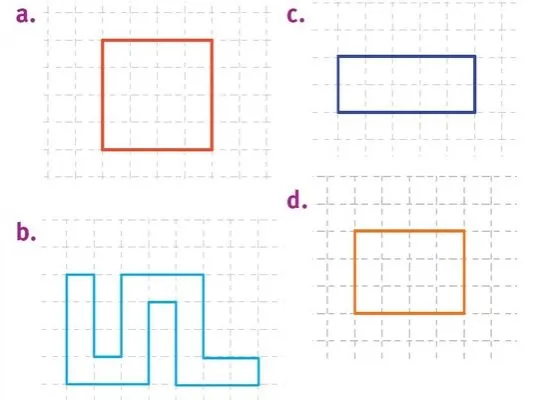


1. Figure a.
2. Figure b.
3. Figure c.
4. Figure d.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
Effectuer les calculs suivants, en faisant bien attention aux unités.
1. 2,3 m + 42,3 cm
2. 45,3 cm + 15 mm
3. 42,3 dm + 18 cm
4. 42,3 km + 321 dam
5. 42,3 cm + 42,3 mm
1. 2,3 m + 42,3 cm
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31
Calculer l'aire.

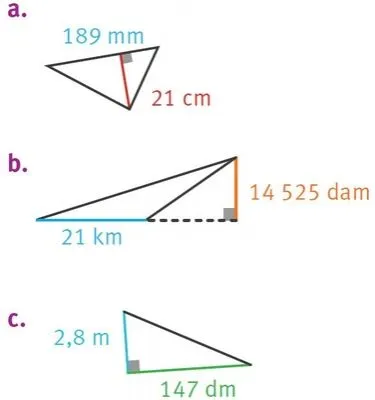
1. Dans les triangles précédents.


1. Dans les triangles précédents.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
Calculer le périmètre et l'aire.

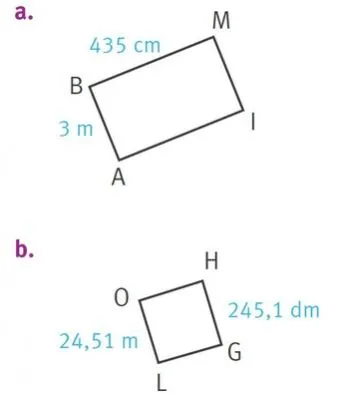

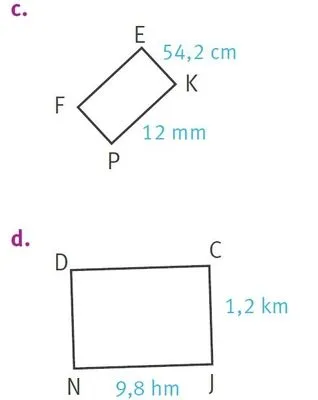
1. Du rectangle a.
2. Du rectangle b.
3. Du rectangle c.
4. Du rectangle d.




1. Du rectangle a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
Comparer les périmètres et les aires de ces figures.
- Un carré de côté 39 cm ;
- un rectangle de longueur 430 mm et de largeur 345 mm ;
- un cercle de rayon 2,47 dm.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
Effectuer les calculs suivants, en faisant bien attention aux unités.
1. 5,2 km \times 342 m.
2. 4,12 cm \times 23 mm.
3. 457 dm \times 12 m.
4. 45,2 dam \times 3,21 hm.
1. 5,2 km \times 342 m.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
Donner le périmètre des polygones suivants.

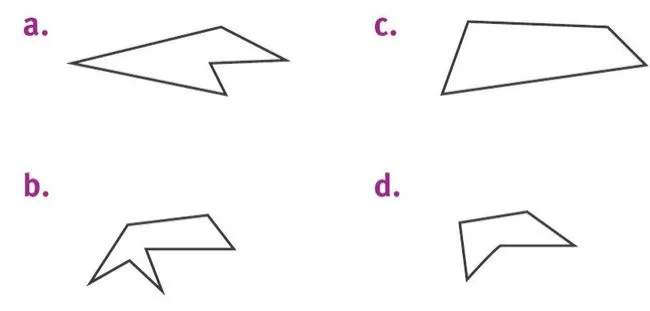
1. En utilisant les instruments de mesure.


1. En utilisant les instruments de mesure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
Donner l'aire des triangles rectangles suivants.

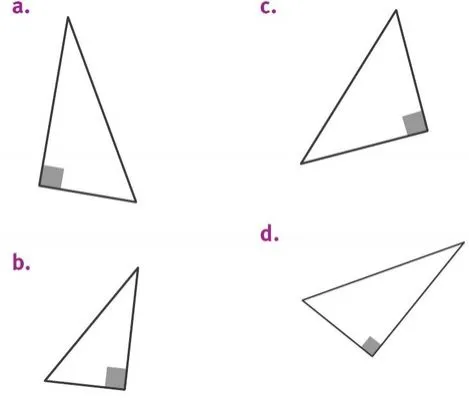
1. En utilisant les instruments de mesure.


1. En utilisant les instruments de mesure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37
Donner l'aire des triangles suivants.

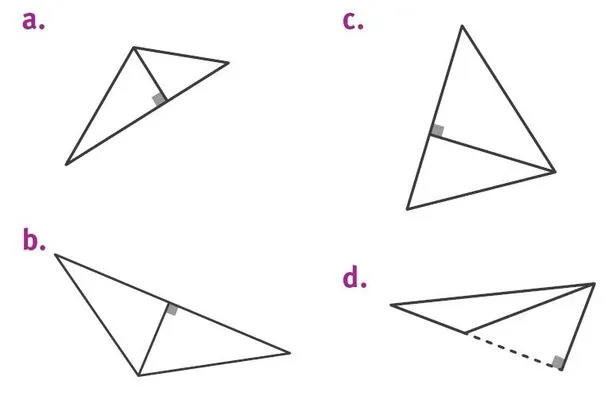
1. En utilisant les instruments de mesure.


1. En utilisant les instruments de mesure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
Julie s'occupe du potager suivants, composé de portions rectangulaires.

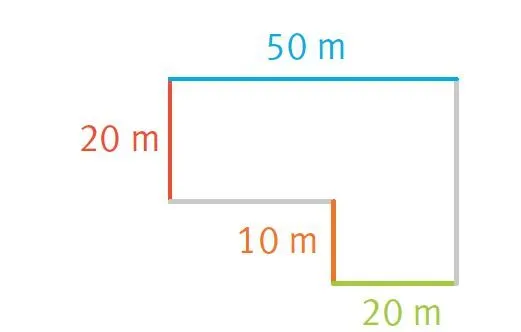
1. Quelle est l'aire de ce potager ?
2. Julie répand sur son potager 2 litres de purin d'ortie par mètre carré. Quel volume de purin va-t-elle utiliser ?


1. Quelle est l'aire de ce potager ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
Donner une valeur approchée au millimètre près.

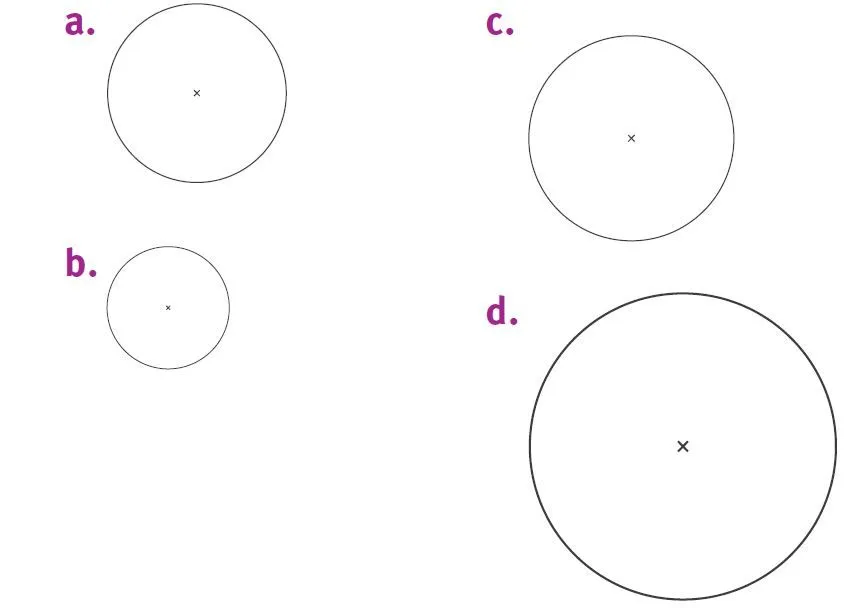 1. Du périmètre de ces cercles.
1. Du périmètre de ces cercles.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
Donner une valeur approchée au centième carré près.

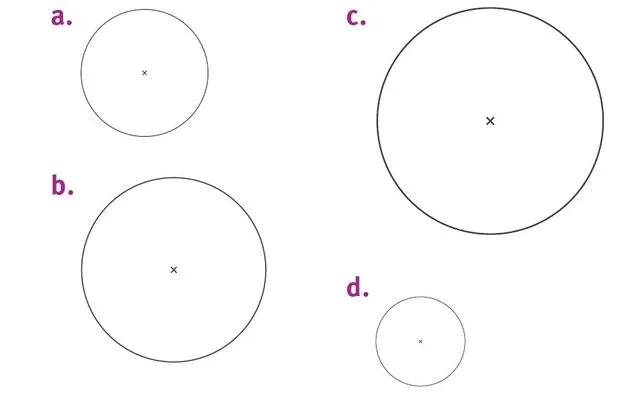 1. De l'aire des disques précédents.
1. De l'aire des disques précédents.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
Vrai ou faux ?
Justifier la réponse.
1. Si deux rectangles ont la même aire, ils ont le même périmètre.
2. Si deux rectangles ont le même périmètre, ils ont la même aire.
3. Si deux carré ont le même périmètre, ils ont la même aire.
1. Si deux rectangles ont la même aire, ils ont le même périmètre.
2. Si deux rectangles ont le même périmètre, ils ont la même aire.
3. Si deux carré ont le même périmètre, ils ont la même aire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
Reproduire la figure suivante.

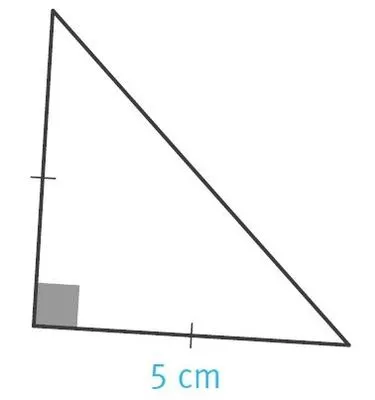
1. Calculer son aire.


1. Calculer son aire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
Construire deux rectangles ayant une aire de 12 cm^2...
1. ... de dimensions en cm entières différentes.
1. ... de dimensions en cm entières différentes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44

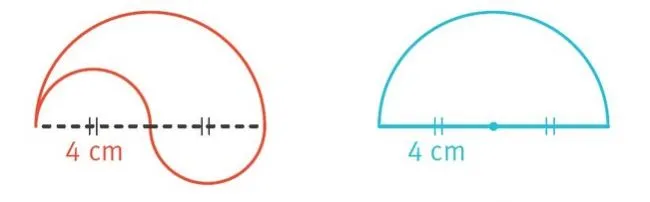
1. Calculer le périmètre et l'aire de la figure rouge.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
Reproduire la figure suivante.

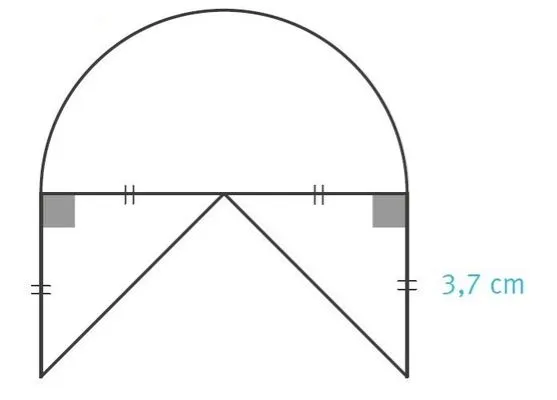
1. Calculer son aire.


1. Calculer son aire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46Histoire et mythologie.


1. Effectuer une recherche sur la manière dont la reine Didon a acquis le terrain sur lequel elle fonda Carthage, selon la légende.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47Isopérimétrie.
1. Compléter le tableau suivant dans un tableur. On pourra aussi le compléter avec des données issues des autres figures de ce manuel ou des figures de la vie courante.
2. Pour chaque ligne, comparer les cases situées dans les deux dernières colonnes. Que remarque-t-on ?
| Figure (dimensions en cm) | Périmètre : P | Aire : A | 4 \times \pi \times A | P \times P |
|---|---|---|---|---|
| Carré de côté de longueur 2 |
|
|
|
|
| Rectangle de dimension 3 et 4 |
|
|
|
|
|
Triangle rectangle dont les côtés adjacents à l'angle droit mesurent 3 et 4 ; le troisième côté mesure 5 |
|
|
|
|
| Cercle de rayon 1 |
|
|
|
|
2. Pour chaque ligne, comparer les cases situées dans les deux dernières colonnes. Que remarque-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
Calculer l'aire et le périmètre d'une feuille A4. Pour chacune des propositions, dire si elle est possible.
1. On peut tracer une figure de 4 m de périmètre sur une feuille A4.
2. On peut tracer une figure de 4 m^2 d'aire sur une feuille A4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
Une seule des deux propositions de l'exercice précédent est vraie.
1. Réaliser la construction proposée.
1. Réaliser la construction proposée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
Question : calculer l'aire et le périmètre de ce triangle rectangle.

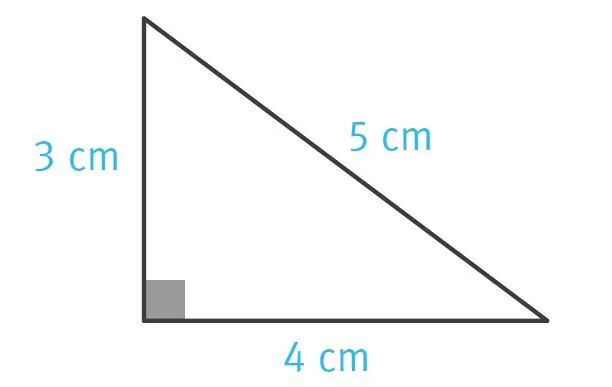

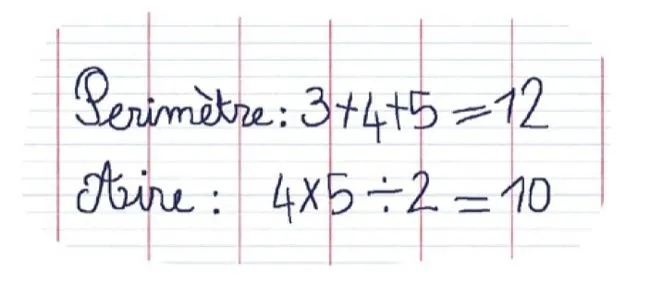
1. La réponse à cet exercice est-elle correcte ? Si ce n'est pas le cas, la corriger.



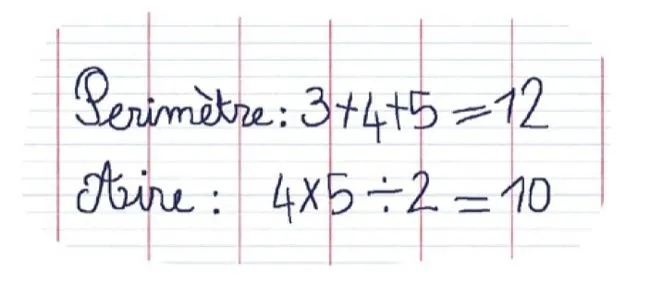
1. La réponse à cet exercice est-elle correcte ? Si ce n'est pas le cas, la corriger.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compétition
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
La ville de Washington (États-Unis d'Amérique) avait à ses débuts la forme d'un carré de 10 milles de côté.
1. Rechercher et exprimer la longueur d'un mille en km.
2. Exprimer la surface d'un mille carré en km^2.
3. En déduire deux manières différentes de trouver l'aire originelle de Washington en km^2.
1. Rechercher et exprimer la longueur d'un mille en km.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
Construire un triangle PUG, tel que PU = 7 cm, UG = 6 cm et GP = 8 cm. Effectuer une construction supplémentaire afin de pouvoir calculer son aire.
1. Quelle est-elle ?
1. Quelle est-elle ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53

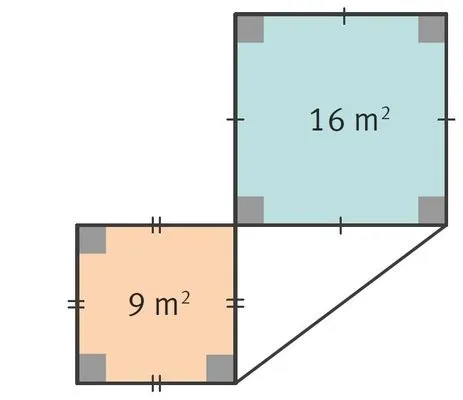
1. Donner l'aire du triangle rectangle précédent sans utiliser d'instrument de mesure !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54Aire du losange.
1. Construire un losange CLAF, tel que FL = 8 cm et CA = 12 cm.
2. Trouver une manière de calculer l'aire du losange CLAF. Justifier la démarche.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55Igor l'agriculteur et ses champs.


1. Calculer le périmètre et l'aire d'un carré de 2 m de côté, puis d'un carré de 4 m de côté.
2. Igor possède deux champs de forme carrée. Le second a des côtés deux fois plus grands que le premier, et a coûté deux fois plus cher. Comparer les prix au m^2 de ces deux champs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
Utiliser la calculatrice pour résoudre cet exercice. La Terre est située en moyenne à 149 597 887 km du Soleil. On suppose que la Terre décrit un cercle autour du soleil. On considère ici qu'un an correspond à un tour.
1. Donner une valeur approchée au km de la distance qu'elle parcourt autour du Soleil en un tour.
2. La Terre parcourt en fait 924 375 700 km environ en un tour autour du Soleil. Est-ce loin du résultat précédent ?
3. Effectuer une recherche sur l'orbite terrestre pour expliquer ce résultat.
1. Donner une valeur approchée au km de la distance qu'elle parcourt autour du Soleil en un tour.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
Au niveau de l'équateur, la Terre a un rayon de 6 378,137 km.
1. À l'aide d'une calculatrice, déterminer la longueur de l'équateur.
1. À l'aide d'une calculatrice, déterminer la longueur de l'équateur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
Une corde fait juste la bonne longueur pour former un cercle de 1 m de rayon.
1. Quelle longueur de corde faut-il rajouter environ pour pouvoir former un cercle de 2 m de rayon ?
2. La corde fait maintenant un cercle de 100 m de rayon. Quelle longueur de corde faut-il rajouter pour pouvoir former un cercle de 101 m de rayon ?
3. On suppose maintenant que la corde est suffisamment longue pour faire le tour de la Terre au niveau de l'équateur. À votre avis, quelle longueur de corde faut-il rajouter pour qu'on puisse la soulever à 1 mètre de hauteur de partout en même temps ? Pourquoi ?
1. Quelle longueur de corde faut-il rajouter environ pour pouvoir former un cercle de 2 m de rayon ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
Voici un schéma représentant le drapeau suisse, qui est de forme carrée.

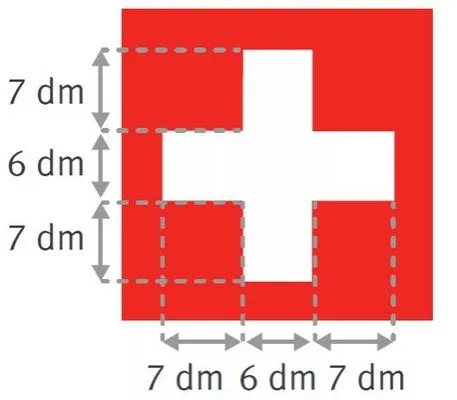
1. Quel est le périmètre de la croix blanche ?
2. Le périmètre du drapeau est 1,5 fois plus grand que le périmètre de la croix. Quelle est l'aire de ce drapeau ?


1. Quel est le périmètre de la croix blanche ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
Ces deux cercles ont le même centre.




1. Expliquer comment faire pour calculer l'aire verte située entre les deux cercles. Justifier la démarche.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Socle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCM
1. 1 dm =
2. 10 m^2 =
3. Pour obtenir le périmètre d'un carré, on :
4. Le périmètre de ce rectangle vaut :

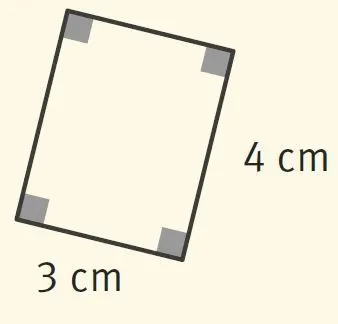
2. 10 m^2 =
3. Pour obtenir le périmètre d'un carré, on :
4. Le périmètre de ce rectangle vaut :


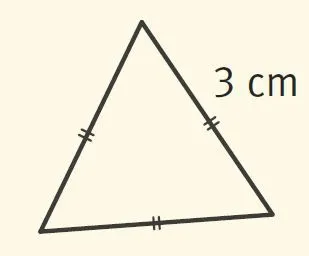
5. Le périmètre de ce triangle vaut :

6. Pour obtenir l'aire d'un rectangle, on :
7. L'aire de ce rectangle vaut :


8. L'aire d'un disque de rayon 1 m vaut :


7. L'aire de ce rectangle vaut :


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Tâche complexe
Clothilde veut clôturer son jardin. Son voisin Robert lui propose d'échanger des parcelles afin qu'elle paie moins cher sa clôture. Que peut-on leur conseiller ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Autour des maths
L'aire et le périmètre d'une figure peuvent avoir des comportements surprenants, surtout dans une fractale ! Le flocon de Koch est une des fractales les plus simples à appréhender, via une construction approchée fondée sur des triangles équilatéraux.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
