Mathématiques Cycle 4
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 5
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35Foot au parc ou au stade ?
✔ Je combine de façon appropriée le calcul mental, posé et instrumenté
✔ Je mène à bien un calcul littéral
Julia organise un foot avec des amis. Elle hésite entre :
✔ Je mène à bien un calcul littéral
Julia organise un foot avec des amis. Elle hésite entre :
- Aller au parc. Il faut alors compter 1,50 € de tickets de métro par personne et 14 € pour faire entrer tout le groupe dans le parc.
- Aller au stade. Il faut alors payer 3 € de tickets de bus par personne, mais une aide de 10 € est apportée par le club.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Le plus rapide est de modéliser la situation avec une inéquation, puis de résoudre lʼinéquation.
Corrigé 1
x correspond au nombre de participants. Les expressions suivantes donnent le prix de la sortie pour chaque solution :
1\text{,}5x + 14 \lt 3x - 10
1\text{,}5x - 1\text{,}5x + 14 + 10 \lt 3x -1\text{,}5x - 10 + 10
14+10\lt3 x-1,5 x
24\lt1,5 x
16\lt x
Nous avons donc la relation 1,5x + 14 \lt 3x-10 si 16 \lt x. Cela signifie qu'aller au parc (1,5x + 14) est moins cher qu'aller au stade (3x-10) s'il y a strictement plus de 16 participants.
- Aller dans un parc coute 14 € en plus des 1,50 € de tickets de métro par personne. Le cout total est donc donné par lʼexpression 1\text{,}5x + 14.
- Aller dans un stade coute 3 € de tickets de bus par personne, mais 10 € seront offerts par le club. Le cout total est donc donné par lʼexpression 3x - 10.
1\text{,}5x + 14 \lt 3x - 10
1\text{,}5x - 1\text{,}5x + 14 + 10 \lt 3x -1\text{,}5x - 10 + 10
14+10\lt3 x-1,5 x
24\lt1,5 x
16\lt x
Nous avons donc la relation 1,5x + 14 \lt 3x-10 si 16 \lt x. Cela signifie qu'aller au parc (1,5x + 14) est moins cher qu'aller au stade (3x-10) s'il y a strictement plus de 16 participants.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
À lʼaide dʼun tableur, il est très facile de calculer le cout de chaque solution, puis de les comparer à lʼaide dʼun graphique.
Corrigé 2
Nous avons vu dans le corrigé 1 que le cout de chaque solution peut être modélisé de la façon suivante, avec x le nombre de participants :

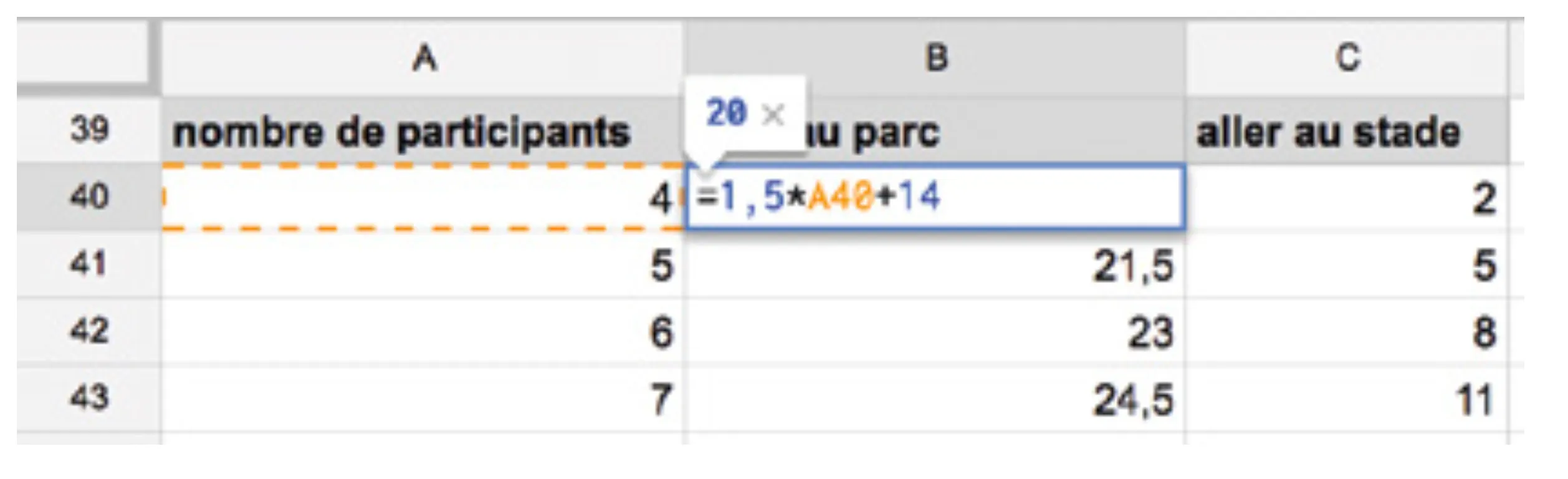
Créons un graphique avec toutes les valeurs obtenues.

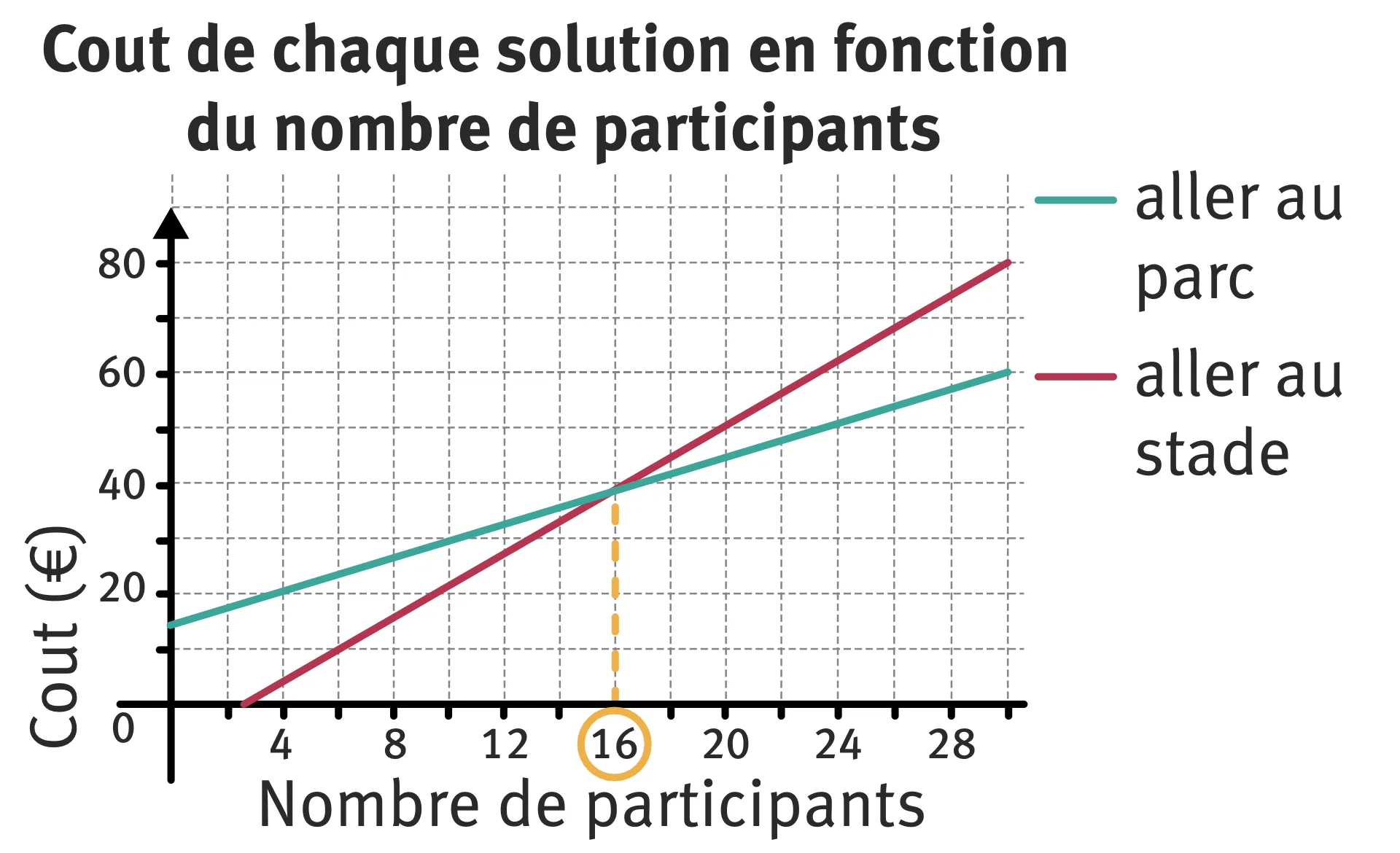
La courbe bleue croise la rouge au point dʼabscisse 16, puis passe en dessous. Il est donc moins cher dʼaller au parc dès que plus de 16 participants sont présents.
- Cout dʼaller au parc : 1\text{,}5x + 14.
- Cout dʼaller au stade : 3x - 10.


Créons un graphique avec toutes les valeurs obtenues.


La courbe bleue croise la rouge au point dʼabscisse 16, puis passe en dessous. Il est donc moins cher dʼaller au parc dès que plus de 16 participants sont présents.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème similaireVoir p. 118 : Locations de films.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
