Dans une piscine, il y a deux bassins. On décide de vider le premier bassin. À lʼorigine, il contient 600 m³ dʼeau. Il se vide 9 m³ dʼeau par minute. Le deuxième bassin, lui, était vide et on choisit de le remplir. Il reçoit 3 m³ dʼeau par minute.

Après combien de minutes y a-t-il la même quantité dʼeau dans les deux bassins ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

37
Résultats en mathématiques.

Noé a eu deux notes en mathématiques. Entre les deux, il a progressé de 3 points et sa moyenne est de 14.

1. n est sa note de mathématiques la plus basse. Comment peut-on alors écrire en fonction de n sa deuxième note ?

2. Exprimez la moyenne de Noé en fonction de n. Quelle égalité obtient-on alors ?

3. Calculez la note la plus faible de Noé puis sa meilleure note.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

38
Le ruban de Maud.

Maud a un ruban de 10 cm de longueur. Elle donne à chacun de ses trois amis un bout de longueur x.

1. Exprimez la longueur restante de ruban en fonction de x.

2. Après avoir partagé, il lui reste 4 cm de ruban. Quelle longueur a-t-elle donnée à chacun de ses amis ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

39
Rangement.

Dorothée décide de ranger lʼensemble de ses DVD sur des étagères. Après avoir rempli 4 étagères complètement, il lui reste 3 DVD dans les mains.

Sachant que Dorothée possède 51 DVD et quʼelle a mis exactement le même nombre de DVD sur chaque étagère, calculez le nombre de DVD posés sur chacune des étagères.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

40
Distribution de biscuits.

Illustration d'un biscuit en forme de bonhomme

Le zoom est accessible dans la version Premium.

Fred a un paquet de biscuits qui en contient 36. Il en partage un certain nombre avec ses frères.

1. Il donne le même nombre de biscuits à chacun de ses trois frères. Exprimez à lʼaide dʼune expression littérale combien de biscuits il lui reste.

2. Quel nombre de biscuits faut-il donner à chacun de ses frères pour quʼil lui reste autant de biscuits quʼil en a distribués ?

3. Quel nombre de biscuits doit-il donner à chacun de ses frères sʼil veut partager équitablement entre eux quatre ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

41
Rangement de livres.

David décide de ranger lʼensemble de ses livres dans des cartons. Après avoir rempli 6 cartons complètement, il lui reste 4 livres dans les mains.

1. Sachant que David possède 226 livres et que chaque carton peut contenir exactement le même nombre de livres, calculez le nombre de livres que David a rangé dans chacun des cartons.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

42
Entreprise de transport.

Lʼentreprise Transportation possède 35 véhicules : des camions et des camionnettes.

1. Sachant que lʼentreprise a 1,5 fois plus de camionnettes que de camions, calculez le nombre de camions et le nombre de camionnettes que possède lʼentreprise.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

43
Deux bougies.

La première bougie a une hauteur de 20 cm. Quand on lʼallume, elle diminue de 2,35 cm par heure. La deuxième bougie a une hauteur de 10 cm. Quand on lʼallume, elle diminue de 0,75 cm par heure.

1. On allume les deux bougies en même temps. Après combien dʼheures auront-elles exactement la même hauteur ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

44
Aller à l'université.

Les étudiants de lʼuniversité Lagrange sont nombreux le matin à venir en moto ou en voiture. Sur le parking de lʼuniversité, on compte tous les matins 41 voitures et 290 roues. On note m le nombre de motos garées sur le parking de lʼuniversité.

1. Combien y a-t-il de motos sur le parking de lʼuniversité ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

45
Savoir refaire
La course.

Le lapin accorde une avance de 200 m au hérisson. La vitesse moyenne du lapin est de 13 m/s, celle du hérisson est de 5 m/s.

1. Combien de temps faut-il au lapin pour rattraper le hérisson ?

2. Qui sera en tête au bout de 300 m ? Au bout de 400 m ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

46
Gérer son épargne.

Catherine a une épargne de 412 € et, chaque mois, elle met 12 € de côté. Naomi a épargné 316 € et, chaque mois, elle met 20 € de côté.

1. Après combien de mois les deux filles ont-elles les mêmes économies ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

47
Le porte-monnaie de Floriane.

Floriane a 40 € dans son portefeuille : en tout, 2 billets et 12 pièces.

Coup de pouce

Testez les différentes combinaisons possibles. Floriane peut-elle avoir deux billets de 20 € ? Un billet de 10 € et un de 20 € ? Un billet de 20 € et un de 5 € ? Deux de 10 € ? Un de 5 € et un de 10 € ? Deux de 5 € ?

1. Sachant quʼelle nʼa que des pièces de 1 et 2 €, quels billets a-t-elle ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

48
Valentine dit à sa petite sœur :

« Si tu multiplies par 3 ton âge et que tu lui retranches 4, tu obtiens le double de lʼâge que tu auras dans 2 ans. »

1. Quel est lʼâge de la petite sœur de Valentine ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

49
Naufrage

30 naufragés sont sauvés par un bateau qui passe. Sans les naufragés, les réserves dʼeau sur le bateau auraient été suffisantes pour 60 jours. Avec les naufragés, il nʼy a de lʼeau que pour 50 jours. On note A les réserves dʼeau en litres, p le nombre de passagers quʼil y avait sur le bateau avant lʼarrivée des naufragés et c la consommation dʼeau quotidienne dʼeau par personne.

1. Expliquez pourquoi on a lʼégalité A = 60 \times p \times c.

2. Expliquez pourquoi on a lʼégalité A = 50 \times (30 + p) \times c.

3. Posez une équation.

4. Combien de personnes y avait-il initialement sur le bateau ? (Notez que, de manière logique, on a c > 0.)

5. Quelles sont les réserves dʼeau sur le bateau le jour où les naufragés sont sauvés si un passager consomme 40 L dʼeau par jour ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

50
Camille, 15 ans, souhaite connaitre l'âge de sa grand-mère.

Illustration d'une grand-mère assise dans un fauteuil bleu

Le zoom est accessible dans la version Premium.

Cette dernière aime les énigmes mathématiques. Elle lui répond alors : « Si tu multiplies par 3 mon âge et que tu lui retranches 10 fois le tien, tu obtiens exactement le nombre de bougies que jʼai soufflé à mon dernier anniversaire, cʼest-à-dire mon âge actuel ! ».

1. En posant a lʼâge de la grand-mère de Camille, aidez-la à le calculer.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

51
Le rectangle de Marianne

Copie de Marianne, on y distingue un rectangle, suivit de plusieurs formules et d'une phrase écrite : (x + 3x) × 2 = 100; 7x = 100; x = 100 ÷ 7; x environ = 14,3; La longueur du rectangle est de 14,3 cm environ.

Le zoom est accessible dans la version Premium.

Marianne veut former un rectangle trois fois plus long que large avec un lacet de 100 cm. Elle se demande quelle longueur choisir.

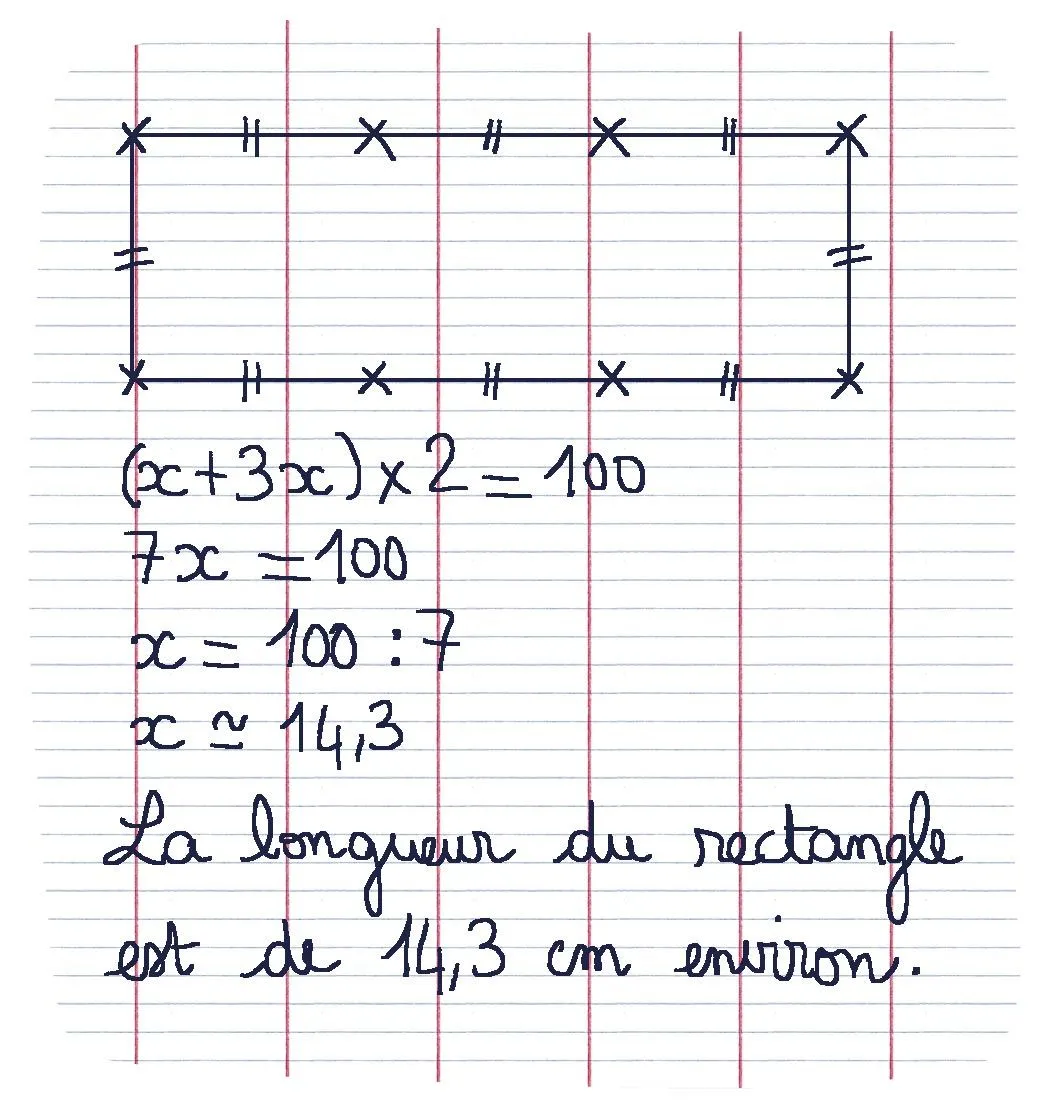
1. Le calcul de Marianne est-il correct ? Dans le cas contraire, corrigez-le.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

52
Joachim et ses gobelets.

Joachim a acheté un paquet de 30 gobelets empilés. Un gobelet mesure 12 cm de haut. Lʼensemble du paquet mesure 32,3 cm de haut.

1. Faites le schéma dʼun empilement de 5 gobelets et introduisez une inconnue.

2. Calculez la longueur dʼun paquet de gobelets du même type contenant 50 gobelets.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

53
Savoir refaire
Boite à bijoux.

Le zoom est accessible dans la version Premium.

Emma veut fabriquer une boite à bijoux de forme rectangulaire, deux fois plus longue que large. Elle voudrait avoir un grand compartiment de largeur 10 cm et 7 cases carrées.

1. Quelles dimensions faut-il choisir pour la boite ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

54
La boite du pêcheur.

Le zoom est accessible dans la version Premium.

Un pêcheur souhaite fabriquer une boite respectant les contraintes suivantes : elle doit être carrée et contenir, sur deux rangées, 14 petites cases carrées identiques pour ranger les plombs. Un schéma montre ce qui lui plairait, vu du dessus.

1. Déterminez les dimensions manquantes de la boite pour quʼil puisse la réaliser.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

55
Achat de DVD.

André a reçu un bon de 50 € pour acheter des DVD par internet. Les frais dʼenvoi sont de 8,50 € et chaque DVD coute 6,99 €.

1. Combien de DVD peut-il acheter ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

56
Une belle armoire.

Le zoom est accessible dans la version Premium.

Dans lʼarmoire suivante, tous les tiroirs sont de la même hauteur.

1. Quelle est la hauteur totale de lʼarmoire ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

57
Un bel héritage !

Suite au décès du roi, les trois princes du royaume se partagent un héritage de 8 000 couronnes. Le testament précise toutefois que lʼainé des trois princes doit recevoir 1 000 couronnes de plus que le deuxième et que le deuxième doit recevoir 500 couronnes de plus que le dernier.

1. De quelle somme hérite chacun des princes ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

58
Savoir refaire
Un prince amasse un trésor de guerre de 1 500 pièces d'or.

Généreux, il décide de donner le même nombre de pièces à chacun de ses 87 sujets.

1. Combien de pièces peut-il distribuer à chacun de ses sujets, sachant quʼil veut en garder au minimum 300 ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

59
Le poulailler de Robert.

Le zoom est accessible dans la version Premium.

Robert élève des poules et des coqs. Il sait quʼil possède 6 coqs mais voudrait connaitre le nombre exact de poules quʼil a. Pour cela, il sʼintéresse au nombre dʼœufs quʼil vient de récupérer auprès de ses poules. Il sait que :

un quart de ses poules ne peut pas pondre d'œufs ;
un quart en pond un tous les matins ;
un quart en pond deux ;
le dernier quart en pond trois tous les jours.

Il compte ses œufs du jour et en trouve 48.

Coup de pouce

Notez x le nombre total de poules.
Combien y a-t-il de poules qui ne pondent pas dʼœufs en fonction de x~?

1. Combien Robert possède-t-il de poules ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

60
Partage de bonbons.

Timothée veut partager de façon équitable 24 bonbons entre ses amis et lui-même.

1. Exprimez le nombre de bonbons par personne, à lʼaide dʼune expression littérale, en fonction du nombre dʼamis.

2. Pour quels nombres dʼamis est-il possible de partager de façon équitable ?

3. Chacun obtient 3 bonbons. Combien sont-ils au total ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

61
Exercice : À l'aide d'une feuille carrée.

On découpe une feuille carrée horizontalement et verticalement et on obtient quatre rectangles. La somme de leurs périmètres est de 50 cm.

Coup de pouce

Faites un dessin puis écrivez la formule des périmètres.

Le zoom est accessible dans la version Premium.

1. Déterminez la longueur du côté du carré initial.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

62
Inéquations et problèmes.

1. Résolvez lʼinéquation suivante : 21 +~2x \geq~50.

2. Gabrielle a 21 livres dans sa bibliothèque. Pour la garnir un peu, elle décide de sʼacheter 2 livres tous les mois. Dans combien de temps Gabrielle aura-t-elle plus de 50 livres sur ses étagères ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

63
Périmètre et aire.

Le zoom est accessible dans la version Premium.

Le périmètre du rectangle ci-contre est de 21 cm.

1. Quelle valeur peut-on rechercher ? Quelle inconnue peut-on poser ?

2. Exprimez le périmètre en fonction de cette inconnue.

3. Quelle est la valeur de lʼinconnue que vous avez posée ?

4. Calculez lʼaire du rectangle.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

64
Inéquations et problèmes.

1. Résolvez lʼinéquation suivante : 45 - 3x \leq 5

2. Caroline hérite de son grand-père de 45 bouteilles de vin grand cru. Malheureusement, elle ne peut garder chez elle que 5 bouteilles maximum, faute de place. Elle décide alors dʼen distribuer 3 à chacun de ses amis jusquʼà ce quʼil lui reste moins de 5 bouteilles. À combien dʼamis va-t-elle offrir des bouteilles de vin ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

65
François va faire de l'escalade.

Le zoom est accessible dans la version Premium.

Il grimpe de x mètres toutes les minutes. Au bout de 10 minutes, il accélère : il grimpe alors de x + 0\text{,}20 mètres toutes les minutes. 10 minutes plus tard, un peu fatigué, il fait une pause pendant 2 minutes. Puis il change à nouveau de cadence : il monte alors x mètres toutes les 30 secondes. En une demi-heure, il a parcouru 20 mètres.

Coup de pouce

Raisonnez par étapes :

Exprimez en fonction de x la distance parcourue les 10 premières minutes. Faites de même pour les 10 minutes suivantes.
Pendant combien de temps a-t-il monté à la vitesse de x mètres toutes les 30 secondes ? Combien de mètres parcourt-il alors par minutes ?
Combien de mètres a-t-il parcourus en fonction de x ?

1. Combien de mètres a-t-il gravis pendant les 10 premières minutes ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

66
Consommation d'une voiture.

La voiture A à moteur diesel coute 14 000 € à lʼachat mais ne consomme que 0,12 € dʼessence au kilomètre. En revanche, la voiture B à essence ne coute que 9 000 € à lʼachat mais consomme 0,15 € dʼessence sans plomb au kilomètre.

1. Déterminez à partir de combien de kilomètres parcourus lʼachat de la voiture A est plus avantageux.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

67
Location de films.

Deux sites proposent des formules différentes pour regarder des films en ligne. Le premier site, Movie-Lover, propose de ne payer que 1,40 € par film vu, à condition dʼavoir payé 15 € dʼabonnement. Son concurrent, Watch-a-Movie, ne fait pas payer dʼabonnement, mais cela coute 3,20 € par film.

1. Combien de films faut-il regarder par an au minimum pour quʼil soit plus rentable dʼaller sur Film-Lover plutôt que sur Watch-a-Movie ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

68
Savoir refaire
Abonnement au cinéma.

Un cinéma propose deux formules annuelles dʼabonnement : la formule Alpha et la formule Bêta. Si un client choisit la formule Alpha, il paie initialement une cotisation de 30 € et paiera par la suite chacune de ses places de cinéma 4 €.
La formule Bêta, en revanche, propose une cotisation initiale de 50 € mais un cout de 3 € par place.

On note n le nombre de places de cinéma achetées par le client au cours de lʼannée.
1. Exprimez, en fonction de n, le cout à lʼannée avec la formule Alpha.

2. Exprimez, en fonction de n, le cout à lʼannée avec la formule Bêta.

3. À partir de combien de places achetées dans lʼannée la formule Bêta se révèle-t-elle la plus intéressante ?

4. Peut-on réaliser une économie de 50 % grâce à la formule Bêta ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

69
Argent de poche.

La maman de Noa propose à sa fille trois manières différentes de lui donner de lʼargent de poche.

Si Noa choisit la première formule, elle reçoit chaque mois la somme fixe de 12 €.
Si Noa choisit la deuxième formule, elle reçoit 5 € dʼargent de poche fixe, plus 2 € pour chaque note au-dessus de 15/20 quʼelle obtient au collège.
Si Noa choisit la troisième formule, elle reçoit 3 € pour chaque note au-dessus de‑15/20.

1. Combien de notes au-dessus de 15/20 doit-elle avoir pour que la troisième formule proposée par sa maman soit la plus intéressante ?

2. Combien dʼargent de poche recevra-t-elle alors ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

70
Location de camionnettes.

Une société de location de camionnettes propose la grille de tarifs suivante :

Camionnette	Forfait	Prix par km parcouru
Type A	50 €	1 €
Type B	60 €	0,50 €
Type C	70 €	0,75 €

1. Pour quelle distance en kilomètres le prix de location dʼune camionnette de type A est-il supérieur à celui dʼune location dʼune camionnette de type B mais inférieur à celui dʼune location dʼune camionnette de type C ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

71
Contrat avec un réparateur informatique.

Un réparateur informatique et une grande entreprise décident de signer un contrat pour travailler ensemble durant un an. Le réparateur propose à lʼentreprise deux options.

Avec lʼoption 1, chaque réparation dʼordinateur sera facturée 80 €.
Avec lʼoption 2, chaque réparation sera facturée 50 € mais lʼentreprise sʼengage à verser initialement au réparateur un « forfait » de 3 000 €.

1. Calculez les prix que doit payer lʼentreprise si 250 de ses ordinateurs tombent en panne au cours de lʼannée pour chacune des options.

2. On note n le nombre dʼordinateurs tombés en panne au cours de lʼannée. Exprimez le prix payé dans chacune des options sous la forme dʼexpressions littérales.

3. Si le budget réparation de lʼentreprise est de 4 000 €, combien de pannes peut avoir au maximum lʼentreprise au cours de lʼannée pour chaque option ?

4. Pour quel nombre de pannes dans lʼannée est-il équivalent pour lʼentreprise de choisir lʼoption n°1 ou lʼoption n°2 ?

5. À quelles conditions lʼoption n°2 est-elle préférable pour lʼentreprise ?

6. Entrez ces informations dans un document tableur et, par lecture graphique, retrouvez les résultats des trois questions précédentes.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

72
Château d'eau.

Un château dʼeau a la forme dʼun cône renversé sur un cylindre comme indiqué sur le schéma suivant.

Figure géométrique représentant le château d'eau

Le zoom est accessible dans la version Premium.

On considère que la situation hydrométrique est critique lorsque le château dʼeau est rempli à moins de 60 % de sa capacité totale. Déterminez la hauteur dʼeau h correspondant à ce seuil critique.

Coup de pouce

Calculez les volumes du cône et du cylindre.

Calculez le volume du château dʼeau. Attention à ne pas compter deux fois le même volume !

Calculez le volume correspondant au volume limite.

Quelle part du cylindre est-ce ? Quelle part du cône ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

73
Inéquations et géométrie.

Le zoom est accessible dans la version Premium.

1. Calculez lʼaire du carré ci-contre. Exprimez lʼaire A du triangle rouge en fonction de celle de x.

Coup de pouce

Exprimez dʼabord lʼaire du triangle rouge en fonction de lʼaire du carré et des aires dʼautres triangles.

2. Pour quelles valeurs de x lʼaire A du triangle rouge est-elle inférieure ou égale au quart de lʼaire du carré noir ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

74
Livret jeune.

Côme a placé sur un Livret Jeune un capital de 450 € qui lui rapporte 4 % dʼintérêts tous les ans. Les intérêts ne sont pas capitalisés, cʼest-à-dire quʼil reçoit chaque année la même somme en intérêts.

1. Calculez le nombre de mois que doit attendre Côme pour que son capital placé soit supérieur à 500 €.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Tâche complexe
Consommations électriques.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

La famille de Patrick a une télévision 32 pouces, deux ordinateurs portables, un PC puissant et des appareils éléctroménagers.Sur une période de 6 mois, elle paye 88 € pour la consommation électrique de l'ensemble.

1. Combien dʼappareils éléctroménagers ont-ils ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 1
Cout de la consommation énergétique.

Le cout (C) de la consommation énergétique est : C = Co × P.
Avec Co la consommation en watts \text{(W)} et P le prix en euros pour un watt.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 2
Consommation annuelle.

TV 32 pouces : 120 \text{W}
TV 42 pouces : 145 \text{W}
TV 50 pouces : 190 \text{W}
PC puissant : 300 \text{W}
PC moyen : 120 \text{W}
Ordinateur portable : 50 \text{W}
Appareils éléctroménagers : 30 \text{W}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 3
Cout de la consommation annuelle.

Le zoom est accessible dans la version Premium.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Je résous des problèmes

36Une piscine à deux bassins.

37Résultats en mathématiques.

38Le ruban de Maud.

39Rangement.

40Distribution de biscuits.

41Rangement de livres.

42Entreprise de transport.

43Deux bougies.

44Aller à l'université.

45Savoir refaireLa course.

46Gérer son épargne.

47Le porte-monnaie de Floriane.

48Valentine dit à sa petite sœur :

49Naufrage

50Camille, 15 ans, souhaite connaitre l'âge de sa grand-mère.

51Le rectangle de Marianne

52Joachim et ses gobelets.

53Savoir refaireBoite à bijoux.

54La boite du pêcheur.

55Achat de DVD.

56Une belle armoire.

57Un bel héritage !

58Savoir refaireUn prince amasse un trésor de guerre de 1 500 pièces d'or.

59Le poulailler de Robert.

60Partage de bonbons.

61Exercice : À l'aide d'une feuille carrée.

62Inéquations et problèmes.

63Périmètre et aire.

64Inéquations et problèmes.

65François va faire de l'escalade.

66Consommation d'une voiture.

67Location de films.

68Savoir refaireAbonnement au cinéma.

69Argent de poche.

70Location de camionnettes.

71Contrat avec un réparateur informatique.

72Château d'eau.

73Inéquations et géométrie.

74Livret jeune.

Tâche complexeConsommations électriques.

Énoncé

Doc. 1Cout de la consommation énergétique.

Doc. 2Consommation annuelle.

Doc. 3Cout de la consommation annuelle.

Une erreur sur la page ? Une idée à proposer ?

Nous préparons votre pageNous vous offrons 5 essais

36
Une piscine à deux bassins.

37
Résultats en mathématiques.

38
Le ruban de Maud.

39
Rangement.

40
Distribution de biscuits.

41
Rangement de livres.

42
Entreprise de transport.

43
Deux bougies.

44
Aller à l'université.

45
Savoir refaire
La course.

46
Gérer son épargne.

47
Le porte-monnaie de Floriane.

48
Valentine dit à sa petite sœur :

49
Naufrage

50
Camille, 15 ans, souhaite connaitre l'âge de sa grand-mère.

51
Le rectangle de Marianne

52
Joachim et ses gobelets.

53
Savoir refaire
Boite à bijoux.

54
La boite du pêcheur.

55
Achat de DVD.

56
Une belle armoire.

57
Un bel héritage !

58
Savoir refaire
Un prince amasse un trésor de guerre de 1 500 pièces d'or.

59
Le poulailler de Robert.

60
Partage de bonbons.

61
Exercice : À l'aide d'une feuille carrée.

62
Inéquations et problèmes.

63
Périmètre et aire.

64
Inéquations et problèmes.

65
François va faire de l'escalade.

66
Consommation d'une voiture.

67
Location de films.

68
Savoir refaire
Abonnement au cinéma.

69
Argent de poche.

70
Location de camionnettes.

71
Contrat avec un réparateur informatique.

72
Château d'eau.

73
Inéquations et géométrie.

74
Livret jeune.

Tâche complexe
Consommations électriques.

Doc. 1
Cout de la consommation énergétique.

Doc. 2
Consommation annuelle.

Doc. 3
Cout de la consommation annuelle.