Mathématiques Cycle 4
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 15
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22 Alison et son aquarium.
✔ J'envisage plusieurs méthodes de résolution
✔ Je structure mon raisonnement

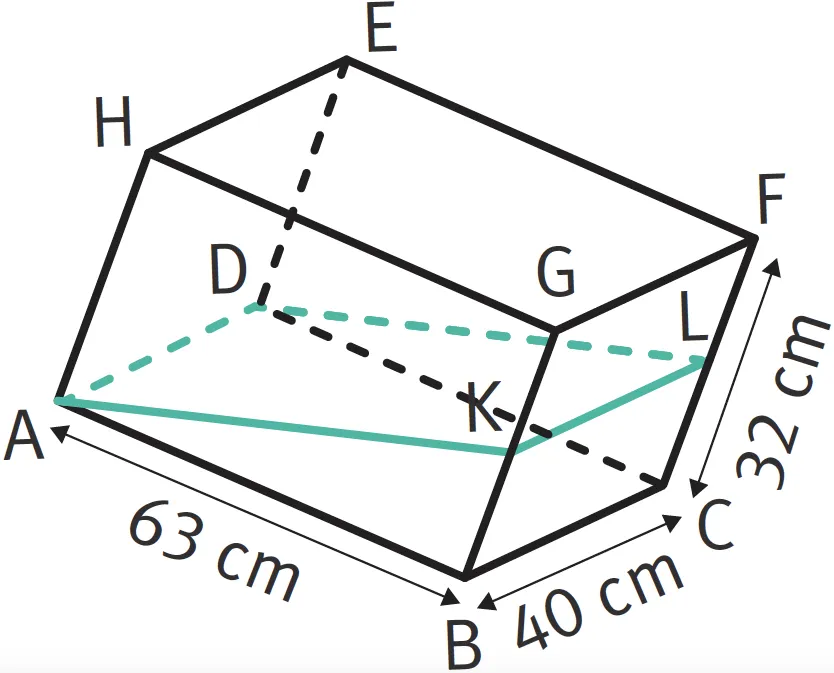 BG = 2BK et CF = 2CL
BG = 2BK et CF = 2CL
(AD) // (KL).
✔ Je structure mon raisonnement


(AD) // (KL).
Alison commence à remplir son aquarium. Elle sʼarrête au milieu du remplissage et lʼobserve. Curieuse, elle se demande quelle est lʼaire de la surface de lʼeau.
Pouvez-vous la trouver pour elle ?
Aide
De manière générale, lorsquʼun schéma avec beaucoup dʼinformations vous est présenté, il est important que vous le redessiniez au brouillon pour vous lʼapproprier et vous assurer que vous avez bien vu toute les informations importantes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Pour calculer lʼaire dʼune figure, la solution la plus rapide est de déterminer si cʼest une figure particulière et de trouver alors les dimensions nécessaires pour en calculer lʼaire.
Corrigé 1
- (KL) est parallèle à (AD) donc à (BC). Donc (KL) est perpendiculaire à (BG). Or la section dʼun pavé droit par un plan qui coupe perpendiculairement une de ses faces est un rectangle. Donc ADLK est un rectangle.
- On sait que AD est une largeur de lʼaquarium donc AD = 40 cm.
- Il nous reste à calculer la longueur AK. Puisque lʼaquarium est un pavé droit, le triangle ABK est rectangle en B. On sait que AB = 63 cm et
BK =\div{1}{2} BG = 32 \div 2 = 16.
Grâce au théorème de Pythagore, on peut écrire :
AK = \sqrt{\text{AB}^2 + \text{BK}^2}
AK = \sqrt{63^2 + 16^2} = \sqrt{4\:225} =65
AK mesure donc 65 cm. - Pour calculer lʼaire de ADLK, il nous faut donc multiplier la longueur du rectangle par sa largeur, soit :
\text{AK} \times \text{KL} = 40 \times 65 = 2\:600
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Une solution (plus longue) permet cependant de mieux se représenter la situation : en traçant lʼaquarium à lʼaide dʼun logiciel de géométrie dynamique.
Corrigé 2
Pour plus de facilité, on représente le pavé droit sur un schéma.
Il faut :
Or, comme toutes les unités sont exprimées en centimètre, on peut en déduire que la superficie de la surface de lʼeau dans lʼaquarium vaut 2 600 cm^2.
Il faut :
- Créer les points A, B, C, D, E, F, G, H, K et L avec les bonnes coordonnées ;
- Créer un pavé droit de base ABCD et de hauteur H ;
- Créer un polygone ADLK ;
- Faire afficher à un logiciel de géométrie dynamique la valeur de lʼaire de ADLK.
Or, comme toutes les unités sont exprimées en centimètre, on peut en déduire que la superficie de la surface de lʼeau dans lʼaquarium vaut 2 600 cm^2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème similaireVoir p. 340 : Coupe d'un pavé droit
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
