Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 8
J'apprends
Statistiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ALes termes de la statistique
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Les études statistiques
Définitions
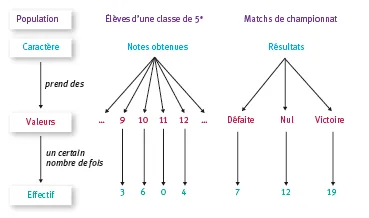
Une enquête statistique se fonde sur lʼobservation dʼune certaine population. Par exemple, les élèves dʼune classe de 5e.
Elle étudie la répartition dʼun caractère au sein de cette population : âge, taille, couleur des cheveux...
Ce caractère peut prendre plusieurs valeurs : une valeur numérique (12 ans, 1,60 m…) ou non (brun...).
Le nombre de fois quʼune valeur est citée constitue son effectif. La somme de tous les effectifs donne lʼeffectif total. Il doit être égal au nombre dʼindividus qui composent la population.
Elle étudie la répartition dʼun caractère au sein de cette population : âge, taille, couleur des cheveux...
Ce caractère peut prendre plusieurs valeurs : une valeur numérique (12 ans, 1,60 m…) ou non (brun...).
Le nombre de fois quʼune valeur est citée constitue son effectif. La somme de tous les effectifs donne lʼeffectif total. Il doit être égal au nombre dʼindividus qui composent la population.
Le zoom est accessible dans la version Premium.
Exercices n° p. 174-175.
J'applique
Consigne :Paul fait une étude statistique sur la couleur de cheveux des élèves de sa classe.
Il compte 17 bruns, 6 blonds et 2 roux.
Quels sont la population, le caractère, les valeurs, les effectifs et lʼeffectif total de cette série ?
Correction :
| Population | les élèves de la classe | ||
| Caractère étudié | la couleur des cheveux | ||
| Valeurs | brun | blond | roux |
| Effectifs | 17 | 6 | 2 |
| Effectif total | 17 + 6 + 2 = 25 | ||
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Classes et fréquences
Définition
Lorsquʼil y a un grand nombre de valeurs possibles pour le caractère de lʼétude statistique, on peut les regrouper en classes. Les classes regroupent plusieurs valeurs. Deux classes ne peuvent pas contenir la même valeur ; on dit donc quʼelles sont disjointes.
Exercices n° p. 175.
J'applique
Consigne : Aïcha veut étudier la taille des 102 élèves présents dans son collège. A-t-elle intérêt à utiliser des classes ?
Correction :
Oui, car elle risque dʼavoir trop de valeurs différentes pour pouvoir les comparer efficacement. Elle peut, par exemple, créer quatre classes :
- Les élèves qui font moins d'1,40 m ;
- Les élèves qui font entre 1,40 m et 1,499 m ;
- Les élèves qui font entre 1,50 m et 1,599 m ;
- Les élèves qui font plus d'1,60 m.
Définition
La fréquence dʼune valeur (ou dʼune classe de valeurs) est la proportion que représente son effectif par rapport à lʼeffectif total. Cʼest un nombre compris entre 0 et 1.
Cette fréquence peut être exprimée en pourcentage, en multipliant le résultat par 100.
\text{Fréquence} = \dfrac{\text{effectif}}{\text{total effectif}}
Cette fréquence peut être exprimée en pourcentage, en multipliant le résultat par 100.
Exercices n° p. 176.
J'applique
Consigne :
Dans la classe de Paul, qui étudiait la couleur des cheveux de ses camarades de classe, quelle était la fréquence de cheveux bruns ?
Correction :
Il y a 17 bruns dans la classe de Paul pour un effectif total de 25 élèves.
\dfrac{17}{25} = 0\text{,}68 = 68 %
Il y a 68 % de bruns dans la classe de Paul.
Remarque : La somme de toutes les fréquences sous forme de pourcentages dʼune étude statistique doit être égale à 100 %.
Aide
Si on a donné des valeurs approchées des fréquences, quand on fait la somme de ces fréquences, on nʼobtient pas forcément 100 %.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BReprésenter les résultats dʼune étude statistique
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Représenter sous forme de tableau
Représentation
Pour présenter les données brutes dʼune étude statistique, il est souvent plus facile dʼutiliser un tableau.
Exercices n° p. 176.
Remarque : Il est important de faire figurer lʼeffectif total pour sʼassurer quʼaucun élément nʼa été oublié : si la somme des effectifs nʼest pas égale à lʼeffectif total, les données ont été mal comptabilisées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Représenter sous forme de diagrammes
Représentation
Il existe de multiples représentations plus visuelles quʼun tableau, notamment :
- Les diagrammes en bâton et les histogrammes : les hauteurs des bâtons sont proportionnelles aux fréquences des classes ;
- Les diagrammes circulaires : les angles des portions sont proportionnels aux fréquences des classes.
Exercices n° p. 175-176.
Exemple :
On peut représenter lʼétude de Paul graphiquement :
On peut représenter lʼétude de Paul graphiquement :
Le zoom est accessible dans la version Premium.
J'applique
Consigne :
Aïcha utilise des classes pour faire son étude sur les tailles et obtient le tableau suivant :
Exprimez ces données à l'aide dʼun diagramme.
Aïcha utilise des classes pour faire son étude sur les tailles et obtient le tableau suivant :
| Taille (cm) | [140 ; 150[ | [150 ; 160[ | [160 ; 170] | Total |
| Effectif | 25 | 31 | 46 | 102 |
Exprimez ces données à l'aide dʼun diagramme.
Correction :
On représente ce tableau à lʼaide dʼun histogramme.
On représente ce tableau à lʼaide dʼun histogramme.
Le zoom est accessible dans la version Premium.
- [140 ; 150] représente les points compris entre 140 et 150 inclus ;
- [140 ; 150[ représente les points compris entre 140 et 150, 140 inclus mais 150 exclu ;
- ]140 ; 150] représente les points compris entre 140 et 150, 150 inclus mais 140 exclu ;
- ]140 ; 150[ représente les points compris entre 140 et 150 exclus.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
COutils statistiques
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Moyenne
Définition
La moyenne M dʼune série de n éléments x_1, x_2, …, x_n se calcule de la façon suivante :
Dans un calcul de moyenne, si lʼon regroupe les éléments par valeur, on dit que lʼon effectue la moyenne des valeurs pondérées par leurs effectifs.
Le zoom est accessible dans la version Premium.
Exercices n° p. 176-179.
Exemple :
Dans un tournoi de foot, on comptabilise le nombre de buts marqués à chaque match.
| Nombre de buts | 0 | 1 | 2 | 3 | 4 | Effectif total |
| Effectif | 5 | 6 | 4 | 3 | 1 | 18 |
En moyenne, le nombre de buts par match se calcule : \dfrac{5\times0+6\times1+4\times2+3\times3+1\times 4}{18}=1\text{,}5
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Médiane
Définition
Dans une série statistique dont les valeurs sont rangées par ordre croissant, on appelle médiane un nombre qui partage cette série en deux groupes de même effectif.
Exercices n° p. 176-179.
J'applique
Consigne :
Voici une série : 39, 43, 36, 38, 46, 44, 39.
a. Quelle est la médiane de cette série ?
b. Si on ajoute 42 à cette série, quelle est la nouvelle médiane ?
Correction :
a. On classe la série statistique par ordre croissant :
La médiane est donc la valeur de la 4e donnée. Elle vaut donc 39.
Voici une série : 39, 43, 36, 38, 46, 44, 39.
a. Quelle est la médiane de cette série ?
b. Si on ajoute 42 à cette série, quelle est la nouvelle médiane ?
Correction :
a. On classe la série statistique par ordre croissant :
Le zoom est accessible dans la version Premium.
b. La 4,5e donnée nʼexiste pas. La médiane est donc entre la 4e et la 5e donnée.
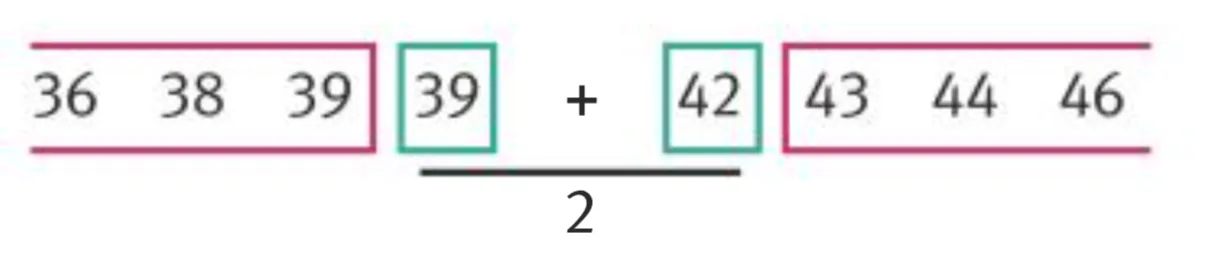Par convention, la médiane que lʼon donne est alors la moyenne des deux valeurs à la limite des deux groupes. On dit donc quʼune médiane de la série est \dfrac{39 + 42}{2} = 40\text{,}5.
Néanmoins, 40 et 41 sont aussi des médianes de cette série.
Le zoom est accessible dans la version Premium.
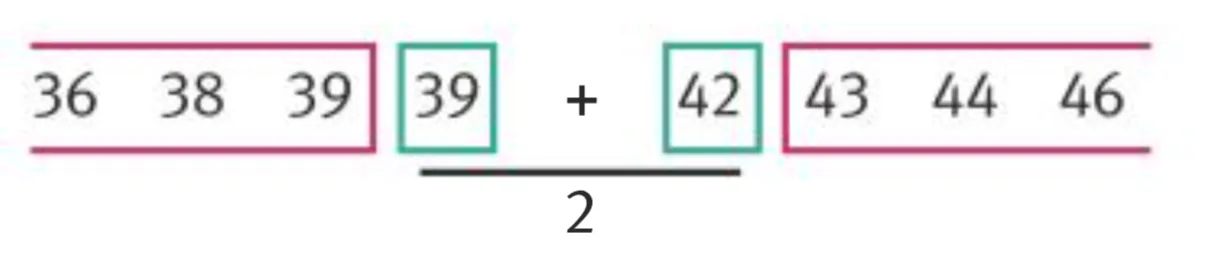
Néanmoins, 40 et 41 sont aussi des médianes de cette série.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3J'approfondisÉtendue
Définition
Lʼétendue dʼune série statistique est lʼécart entre la plus grande valeur et la plus petite valeur de la série. Plus lʼétendue est grande, plus les données de la série sont dispersées.
Exercices n° p. 179.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah