Mathématiques Cycle 4
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 11
Je découvre le chapitre
Transformations dans le plan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1De la symétrie dans le foot
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compétence
Je me repère sur une droite, dans le plan ou dans l'espace
Yasmine montre ses photos de l'Euro 2016 à son cousin Mattéo.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La cérémonie d'ouverture
« – Regarde ! Là c'est quand on a eu la chance avec papa d'avoir des tickets pour le premier match de l'Euro 2016 ! s'exclame Yasmine.
– Veinarde ! répond Mattéo.
– Par contre, nous n'étions pas assis à côté mais dans les tribunes opposées !
– Et tu as aimé ?
– Oh oui ! Surtout la cérémonie d'ouverture : c'était magnifique ! »
– Veinarde ! répond Mattéo.
– Par contre, nous n'étions pas assis à côté mais dans les tribunes opposées !
– Et tu as aimé ?
– Oh oui ! Surtout la cérémonie d'ouverture : c'était magnifique ! »


« Mais du coup vous n'avez pas vu la même chose ! » plaisante Mattéo… Que pensez-vous de son affirmation ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2D'autres transformations du plan
J'approfondis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compétence
Je comprends la modélisation numérique ou géométrique d'une situation
Le grand frère de Mattéo prend des cours à l'auto-école.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 1Bien tenir le volant
L'instructeur lui enseigne qu'il faut poser ses mains sur le volant à « 10 h 10 », c'est-à-dire au niveau des points A et B de la figure suivante.


Après avoir effectué un virage à droite, voici la nouvelle position des mains de Mattéo.

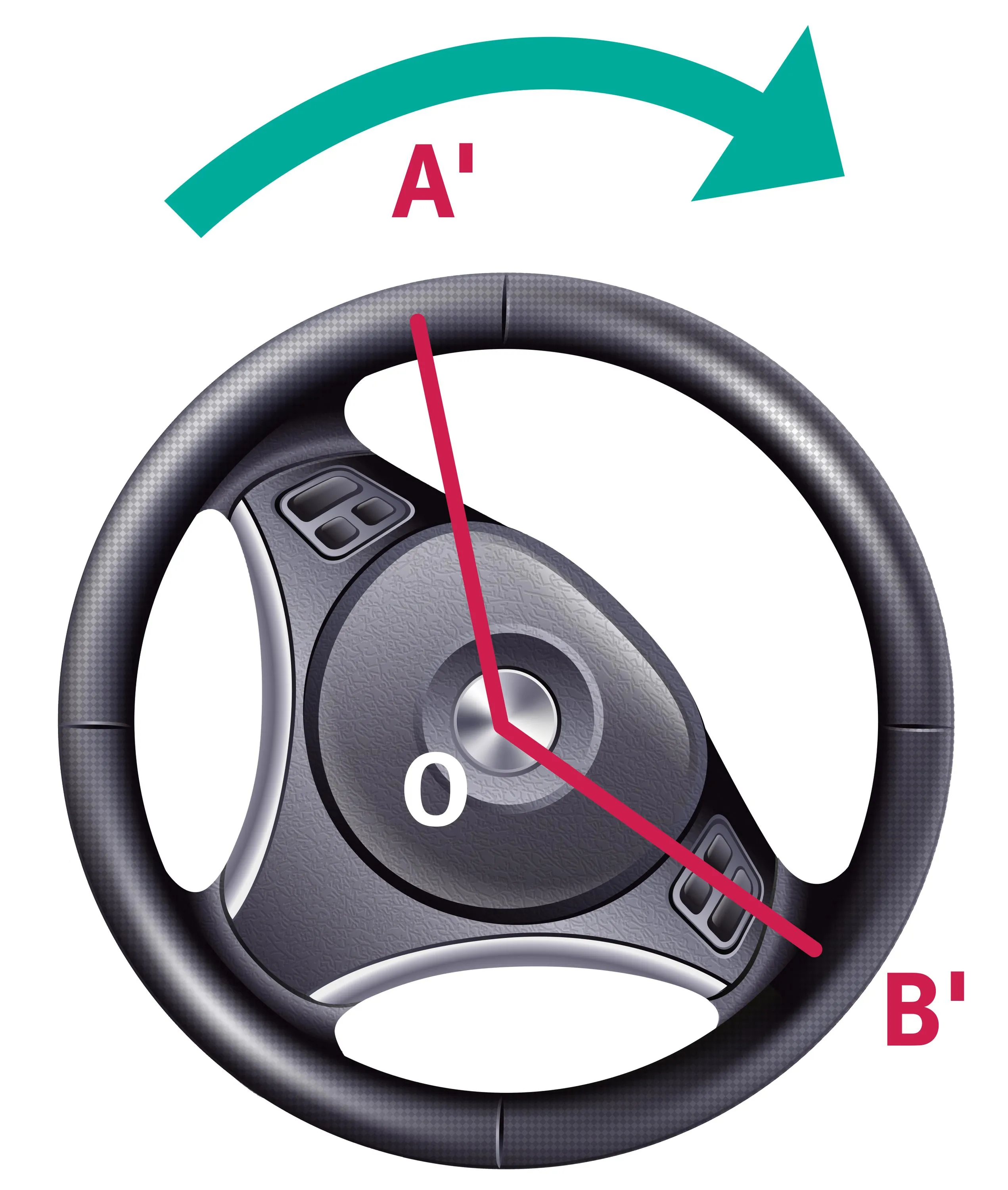


Après avoir effectué un virage à droite, voici la nouvelle position des mains de Mattéo.


1
a. Quelle est la partie du volant qui n'a pas bougé lors de ce mouvement ?2
a. Que remarquez-vous pour les angles \widehat{\text{AOB}} et \widehat{\text{A}^{\prime}\text{OB}^{\prime}} ?Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 2Une descente tout schuss !
Mattéo et Yasmine passent leurs vacances à la montagne. Toute fière, Yasmine montre à Mattéo les progrès qu'elle a fait en suivant les cours de ski. Elle dévale alors la piste noire tout droit.
1
Quel mouvement a suivi Yasmine pour passer du haut de la piste au bas de la piste ?2
La longueur des skis de Yasmine a-t-elle changé pendant la descente ? Déduisez-en une première propriété de conservation de la translation.3
Tout le long de la piste, Yasmine, qui a suivi les conseils de son moniteur, a maintenu ses bâtons de ski avec un angle de 30°. Déduisez-en une autre propriété de conservation de la translation.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 3Le sténopé de Mattéo
Je perfectionne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compétence
Je structure mon raisonnement
En fouillant dans le grenier de sa grand-mère, Mattéo découvre un appareil qui ressemble à une petite valise.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 1Elle sert à quoi, cette valise ?
Mattéo appelle sa cousine Yasmine :
« – Regarde la valise que j'ai trouvée dans le grenier.
– Ce n'est pas une valise ! C'est un sténopé, la fameuse camera obscura inventée par Léonard de Vinci. C'est l'ancêtre de l'appareil photo ! »
« – Regarde la valise que j'ai trouvée dans le grenier.
– Ce n'est pas une valise ! C'est un sténopé, la fameuse camera obscura inventée par Léonard de Vinci. C'est l'ancêtre de l'appareil photo ! »


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 2Les maths à la rescousse !
« - Dans ce cas, dit Mattéo, si je souhaite obtenir une image deux fois plus petite d'un objet, où dois-je alors positionner le sténopé ?
- Facile, répond Yasmine, c'est une homothétie !
- Une quoi ?
- Une homothétie. C'est une transformation qui permet de réduire ou d'agrandir une figure. Un peu comme le zoom de ton appareil photo ! »
- Facile, répond Yasmine, c'est une homothétie !
- Une quoi ?
- Une homothétie. C'est une transformation qui permet de réduire ou d'agrandir une figure. Un peu comme le zoom de ton appareil photo ! »

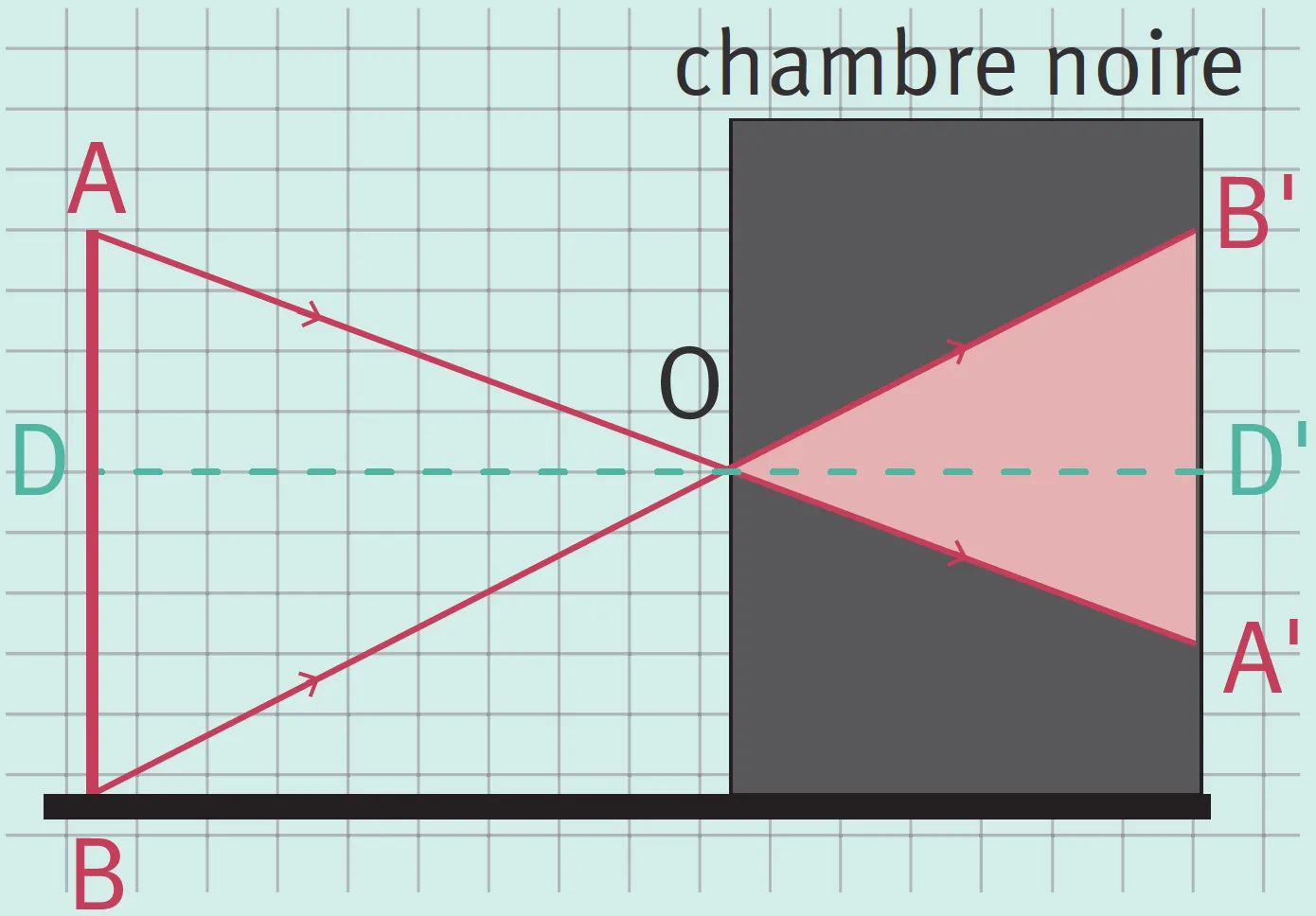
1
Pour quelles valeurs de k aura-t-on un agrandissement ? Une réduction ?2
Pouvez-vous, dans ce cas, répondre à la question de Mattéo ?Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
