Sommaire

Mes pages

Ouverture

p. 1-12

Thème 1 : Nombres et calculs

Testez le chapitre 100 % débloqué

Ch. 1

Arithmétique

Ch. 2

Nombres relatifs

Ch. 3

Nombres fractionnaires

Ch. 4

Calcul littéral

Ch. 5

Équations et inéquations

Ch. 6

Proportionnalité

Ch. 7

Puissances

Thème 2 : Organisation et gestion de données

Ch. 8

Statistiques

Ch. 9

Probabilités

Ch. 10

Fonctions

Thème 3 : Grandeurs et mesures

Ch. 11

Grandeurs et mesures

Thème 4 : Espace et géométrie

Ch. 12

Transformations dans le plan

Ch. 13

Triangles

Ch. 14

Angles et droites parallèles

Ch. 15

Géometrie dans l'espace

Ch. 16

Théorème de pythagore

Ch. 17

Agrandissements - réductions

Ch. 18

Trigonométrie

Annexes

Livret algorithmique et programmation

Pistes EPI

Dossier brevet

Nos dossiers d'actualité

Dossier d'actualité

Page précédente

Chapitre 3

J'apprends

Nombres fractionnaires

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Quʼest-ce quʼune fraction ?

Je découvre

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
La fraction comme proportion

Définition

Une fraction peut représenter un partage, le rapport de proportionnalité entre deux nombres.

Exercices n° 1 à 9
p. 60 et 61

J'applique

Consigne :
Donnez la fraction qui représente le partage.

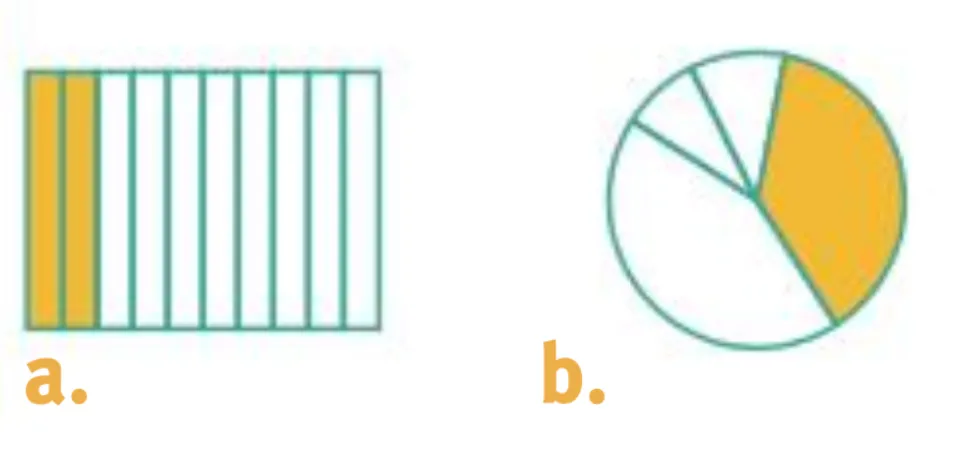
Diagramme comparatif : rectangle divisé en 10 parties, 2 jaunes, et cercle en 4 parties inégales, une grande partie jaune.

Correction :
a.

\frac{2}{10}

\frac{1}{5}

si lʼon regroupe les barres par deux.
b. Ce nʼest pas

\frac{1}{4}

du gâteau. On ne peut pas savoir la fraction que cela représente car il nʼest pas coupé en parts égales.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
La fraction comme quotient et comme nombre

Définition

a

b

sont deux nombres tels que

b

est différent de

0

.
Le quotient de

a

par

b

est le nombre qui, multiplié par

b

, donne

a

. Il est noté

\frac{a}{b}

et est appelé fraction.
Une fraction est donc le résultat dʼune division (avec

a

le numérateur et

b

le dénominateur) :

\frac{a}{b} = a \div b

$Placeholder pour Illustration: fraction a/b, numérateur 'a' et dénominateur 'b', équivaut à a divisé par b.$ $Illustration: fraction a/b, numérateur 'a' et dénominateur 'b', équivaut à a divisé par b.$

Exercices n° 12 à 21
p. 61-63

Aide

Il est impossible de diviser par zéro. Le dénominateur ne peut donc jamais être égal à zéro.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
3. Règles dʼécriture

Vocabulaire

Un nombre rationnel est un nombre qui peut sʼécrire comme une fraction de deux entiers.
Un nombre décimal est la fraction dʼun entier par

10

100

1000

10000

, etc.
Un pourcentage est une fraction de dénominateur

100

.
Certaines fractions ne peuvent pas sʼécrire sous forme décimale car il y aurait un nombre infini de chiffres après la virgule, comme dans le cas de

\frac{1}{3}

. On utilise alors lʼécriture fractionnaire pour donner une valeur exacte. On peut cependant en donner des valeurs décimales approchées.

Exercices n° 12 à 21
p. 61-63

Remarque : Certaines fractions sont des nombres décimaux, comme dans le cas de

\frac{6}{4} = 1, 5

. On dit alors que 1,5 est lʼécriture décimale de la fraction

\frac{6}{4}

J'applique

Consigne :

\frac{1}{7}

peut-il sʼécrire sous forme décimale ?

Correction :

\frac{1}{7}

vaut

0, 142857142857

... avec une infinité de fois

142857

0, 1421857142857 < \frac{1}{7} < 0, 142857142858

. On ne peut pas en donner une écriture décimale exacte. En revanche, on peut en donner une valeur arrondie.

Illustration: approximations décimales de 1/7. Au dixième (0,1), centième (0,14), millième (0,143).

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Comparer des fractions

Je découvre

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Comparaison à zéro

Propriété

On peut repérer une fraction sur une droite graduée.
Une fraction négative se trouve à gauche de 0.

$Placeholder pour Illustration : droite numérique graduée avec des fractions de -1 à 1.$ $Illustration : droite numérique graduée avec des fractions de -1 à 1.$

La règle des signes sʼapplique pour les fractions :

si $a$ et $b$ ont le même signe, alors $\frac{a}{b}$ est positif ;
si les signes de $a$ et $b$ sont différents, alors $\frac{a}{b}$ est négatif.

Exercices n° 24 à 31
p. 63-64

Remarque : On a notamment

- \frac{4}{5} = \frac{- 4}{5} = \frac{4}{- 5}

. Pour un nombre négatif, on préférera la première écriture :

- \frac{4}{5}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Comparer des fractions dans des cas particuliers

Propriété

Une fraction dont le numérateur est égal au dénominateur est égale à 1.
Si deux fractions positives ont le même :

dénominateur, la plus grande est celle qui a le plus grand numérateur.
numérateur, la plus grande est celle qui a le plus petit dénominateur.

Les fractions négatives sont rangées dans le sens contraire des fractions positives.
Si deux fractions ont le même dénominateur, elles sont égales seulement si elles ont le même numérateur.

Exercices n° 24 à 31
p. 63-64

J'applique

Consigne : Comparez

- \frac{5}{7}

- \frac{5}{6}

.

Correction : Les deux fractions ont le même numérateur et

7 > 6

, donc

\frac{5}{7} < \frac{5}{6}

.
Or les deux fractions sont négatives, donc

- \frac{5}{7} > - \frac{5}{6}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Comparaison générale de fractions

Propriété

Si on multiplie ou divise à la fois le numérateur et le dénominateur par le même nombre

k \neq = 0

, alors on ne change pas la valeur de la fraction :

\frac{a}{b} = \frac{a \times k}{b \times k}

\frac{a}{b} = \frac{a \div k}{b \div k}

Exercices n° 24 à 31
p. 63-64

Remarque : Cette propriété permet de comparer des fractions. Cela peut aussi se faire en les plaçant sur une droite graduée ou en donnant leur écriture décimale, lorsque cela est possible.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Simplification de fraction

Propriété

Lorsque le numérateur et le dénominateur dʼune fraction ont un diviseur commun autre que 1, il est possible de simplifier la fraction. Il suffit de diviser le numérateur et le dénominateur par ce diviseur commun.
Si une fraction nʼest pas simplifiable, on dit quʼelle est « irréductible ».

Exercices n° 32 à 35
p. 64

J'applique

Consigne : La fraction

\frac{12}{100}

est-elle simplifiable ?

Correction : 12 et 100 ont un diviseur commun, 4.
Donc

\frac{12}{100} = \frac{3 \times 4}{25 \times 4} = \frac{3}{25}

.
3 et 25 n'ont pas de diviseurs communs, donc

\frac{3}{25}

est irréductible.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

C
Opérations sur les fractions

J'approfondis

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Addition et soustraction

Propriété

Pour additionner ou soustraire des fractions qui ont le même dénominateur, on additionne ou soustrait les numérateurs. Le dénominateur reste le même.
Pour additionner ou soustraire des fractions, on réduit dʼabord les deux fractions au même dénominateur.

Exercices n° 32 à 61
p. 64-67

J'applique

Consigne : Calculez

\frac{2}{9} + \frac{4}{3}

.

Correction :

\frac{2}{9} + \frac{4}{3} = \frac{2}{9} + \frac{4 \times 3}{3 \times 3} = \frac{2}{9} + \frac{12}{9} = \frac{14}{9}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Multiplication de fractions

Rappel

Prendre une fraction dʼun nombre, cʼest le multiplier par cette fraction.

Exercices n° 37 à 61
p. 64-67

Propriété

Pour multiplier deux fractions, on multiplie les numérateurs entre eux et les dénominateurs entre eux.

\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}

Exercices n° 37 à 61
p. 64-67

Exemple : On pose

A = \frac{7}{4} \times 6.

6 = \frac{6}{1}

, on a donc

A = \frac{7}{4} \times \frac{6}{1}

alors

A = \frac{7 \times 6}{4 \times 1} = \frac{6 \times 7}{4}

car

7 \times 6 = 6 \times 7

.
Donc

A = \frac{6}{4} \times 7

J'applique

Consigne : Calculez

\frac{11}{5}

de 15.

Correction : On choisit l'une de ces 3 méthodes :

$\frac{11}{5} \times 15 = 2, 2 \times 15 = 33$ car $\frac{11}{5} = 2, 2$
$\frac{11 \times 15}{5} = \frac{165}{5} = \frac{5 \times 33}{5 \times 1} = 33$
$11 \times \frac{15}{5} = 11 \times 3 = 33$ car $\frac{15}{5} = 3$

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Inverse dʼun nombre

Définition

Lʼinverse dʼun nombre

a

non nul est le nombre qui, multiplié par

a

, donne

1

. Il est noté

\frac{1}{a}

et on a donc :

a \times \frac{1}{a} = 1

.
Lʼinverse dʼun nombre

a

non nul peut également sʼécrire :

a^{- 1} = \frac{1}{a}

Exercices n° 40 à 61
p. 64-67

Remarque : Pour obtenir lʼinverse dʼune fraction, il suffit dʼinverser le numérateur et le dénominateur

(\frac{a}{b})^{- 1} = \frac{b}{a}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Division de fractions

Propriété

Diviser par une fraction, cʼest multiplier par son inverse.

Exercices n° 40 à 61
p. 64-67

Exemple :

\frac{5}{8} \div \frac{27}{13} = \frac{5}{8} \times \frac{13}{27}

\frac{5}{8} \div \frac{27}{13} = \frac{5 \times 13}{8 \times 27} = \frac{65}{216}

Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Arithmétique

Nombres relatifs

Nombres fractionnaires

Calcul littéral

Équations et inéquations

Proportionnalité

Puissances

Statistiques

Probabilités

Fonctions

Grandeurs et mesures

Transformations dans le plan

Triangles

Angles et droites parallèles

Géometrie dans l'espace

Théorème de pythagore

Agrandissements - réductions

Trigonométrie

Livret algorithmique et programmation

Pistes EPI

Dossier brevet

Nombres fractionnaires

A Quʼest-ce quʼune fraction ?

1 La fraction comme proportion

J'applique

2 La fraction comme quotient et comme nombre

3 3. Règles dʼécriture

J'applique

B Comparer des fractions

1 Comparaison à zéro

2 Comparer des fractions dans des cas particuliers

J'applique

3 Comparaison générale de fractions

4 Simplification de fraction

J'applique

COpérations sur les fractions

1 Addition et soustraction

J'applique

2 Multiplication de fractions

J'applique

3 Inverse dʼun nombre

4 Division de fractions

Une erreur sur la page ? Une idée à proposer ?

A
Quʼest-ce quʼune fraction ?

1
La fraction comme proportion

2
La fraction comme quotient et comme nombre

3
3. Règles dʼécriture

B
Comparer des fractions

1
Comparaison à zéro

2
Comparer des fractions dans des cas particuliers

3
Comparaison générale de fractions

4
Simplification de fraction

C
Opérations sur les fractions

1
Addition et soustraction

2
Multiplication de fractions

3
Inverse dʼun nombre

4
Division de fractions