Mathématiques 3e - 2021
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Annexes
Scratch
Dossier brevet
Rappels, Index, Compétences
Révisions Genially
Calcul littéral
Plan de travail
Partie 3 : Espace et géométrie
Chapitre 10
Théorème de Thalès et triangles semblables
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Thalès de Milet est un savant grec né et mort sur les côtes de la Turquie actuelle au VIe siècle av. J.-C.
Pour mesurer la hauteur d'une pyramide, Thalès aurait eu l'idée d'utiliser un bâton planté dans le sol. En mesurant sur le sol les ombres du bâton et de la pyramide et en montrant que les rapports des objets avec leur ombre étaient conservés, il pouvait déduire la hauteur de la pyramide.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectifs du chapitre
- Savoir calculer des longueurs en utilisant le théorème de Thalès dans différentes configurations.
- Montrer que des droites sont ou ne sont pas parallèles.
- Reconnaître des triangles semblables.
- Connaître les effets des agrandissements et réductions sur les longueurs, les angles et les aires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déjà vu
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rappels
1. Soient \text{ABC} un triangle, \text{M} un point appartenant à [\text{AB}] et \text{N} un point appartenant à [\text{AC}] tels que (\mathrm{MN}) // (\mathrm{BC}).
Alors, d'après le théorème de Thalès, on a les égalités de quotients suivantes : {\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{\mathrm{MN}}{\mathrm{BC}}}.
Alors, d'après le théorème de Thalès, on a les égalités de quotients suivantes : {\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{\mathrm{MN}}{\mathrm{BC}}}.

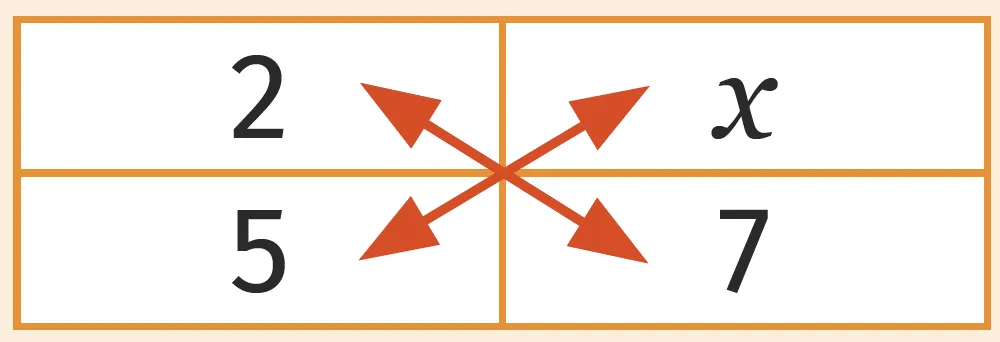
2. Pour calculer une quatrième proportionnelle, on peut utiliser les produits en croix égaux.
Si on a l'égalité. \frac{2}{5}=\frac{x}{7}, on peut utiliser le fait que les produits en croix sont égaux. Ainsi, 5 \times x=2 \times 7 et donc x=\frac{2 \times 7}{5}=2,8.
On retrouve cette propriété dans le tableau de proportionnalité suivant.
Si on a l'égalité. \frac{2}{5}=\frac{x}{7}, on peut utiliser le fait que les produits en croix sont égaux. Ainsi, 5 \times x=2 \times 7 et donc x=\frac{2 \times 7}{5}=2,8.
On retrouve cette propriété dans le tableau de proportionnalité suivant.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Dans les deux cas suivants, déterminer la valeur de x.
1. \frac{3}{5}=\frac{x}{7}
2. \frac{3}{5}=\frac{7}{x}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
On considère un triangle \text{MNP} tel que \mathrm{A} \in[\mathrm{PM}], \mathrm{B} \in[\mathrm{PN}] et (\mathrm{AB}) / /(\mathrm{MN}). Écrire les égalités de quotients de longueurs obtenues grâce au théorème de Thalès.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
On considère la figure suivante.

Compléter les phrases suivantes :
Dans le triangle ... , le point ... appartient au segment [\mathrm{EG}] et le point \text{H} appartient au segment ... . De plus, les droites (\text{FH}) et (\mathrm{GI}) sont ... . Donc, d'après le théorème de ... , on peut écrire les égalités suivantes :\frac{\mathrm{E} \ldots}{\ldots \mathrm{G}}=\frac{\ldots \mathrm{H}}{\mathrm{E} \ldots}=\frac{\ldots}{\ldots}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Soient \text{ABC} un triangle, \text{M} un point de [\mathrm{AB}] et \text{N} un point de [\mathrm{AC}] tels que (\mathrm{MN}) / /(\mathrm{BC}).
1. Si \mathrm{AM}=3 \: \mathrm{cm}, \mathrm{AB}=7 \: \mathrm{cm} et \mathrm{AN}=2 \: \mathrm{cm}, que vaut \text{AC} ?
2. Si \mathrm{AM}=3 \: \mathrm{cm}, \mathrm{MB}=4 \: \mathrm{cm} et \mathrm{BC}=9 \: \mathrm{cm}, que vaut \text{MN} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
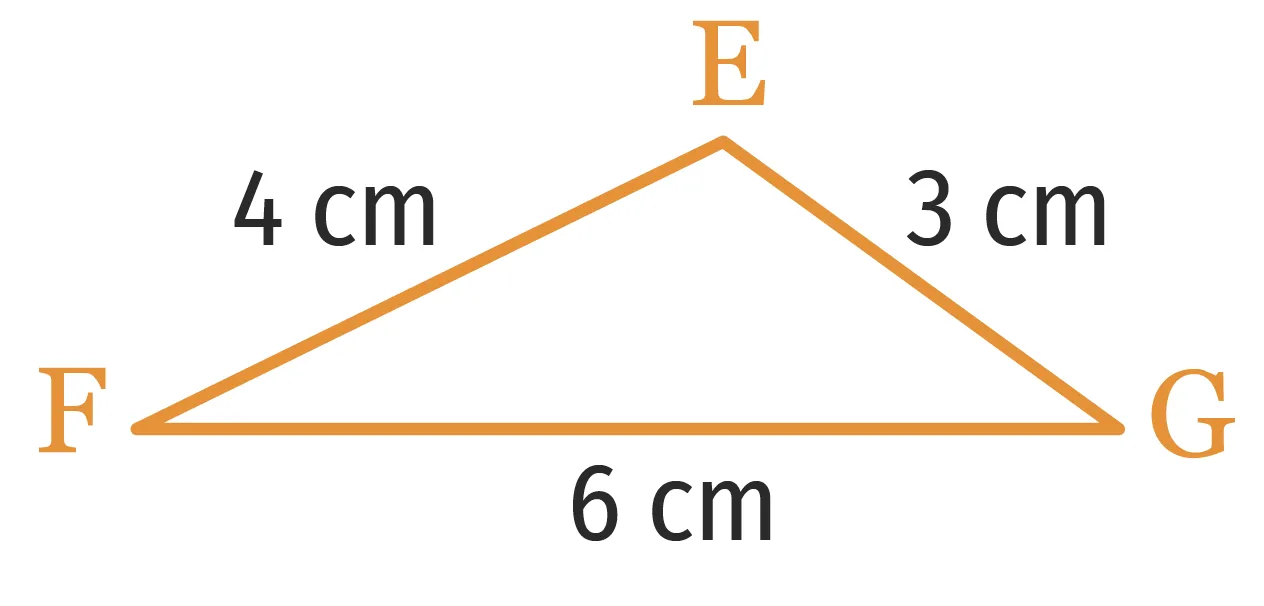
5
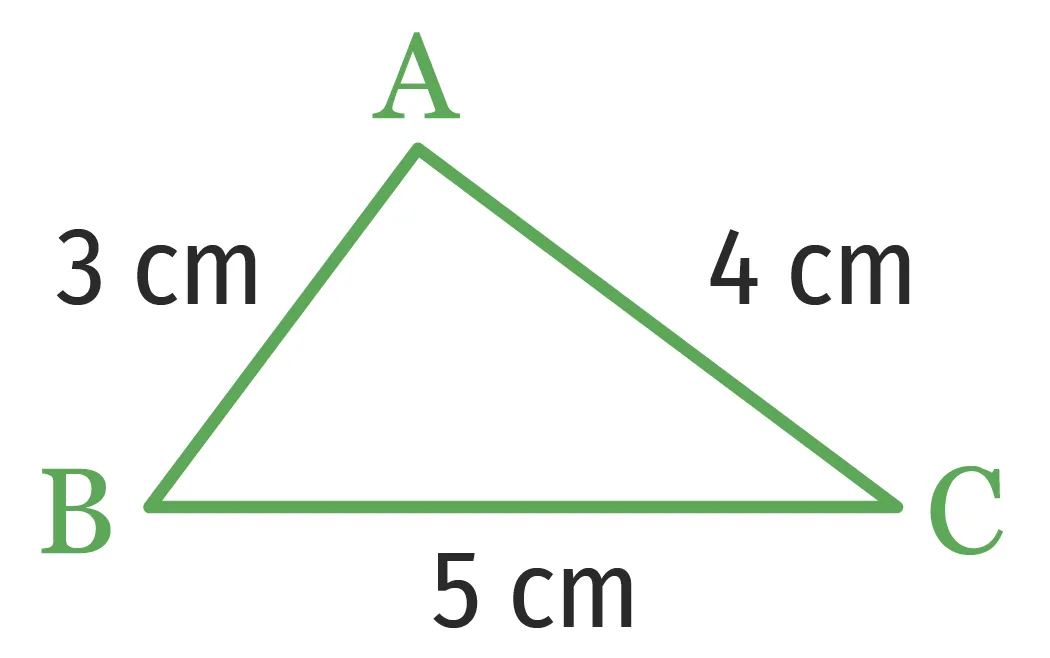
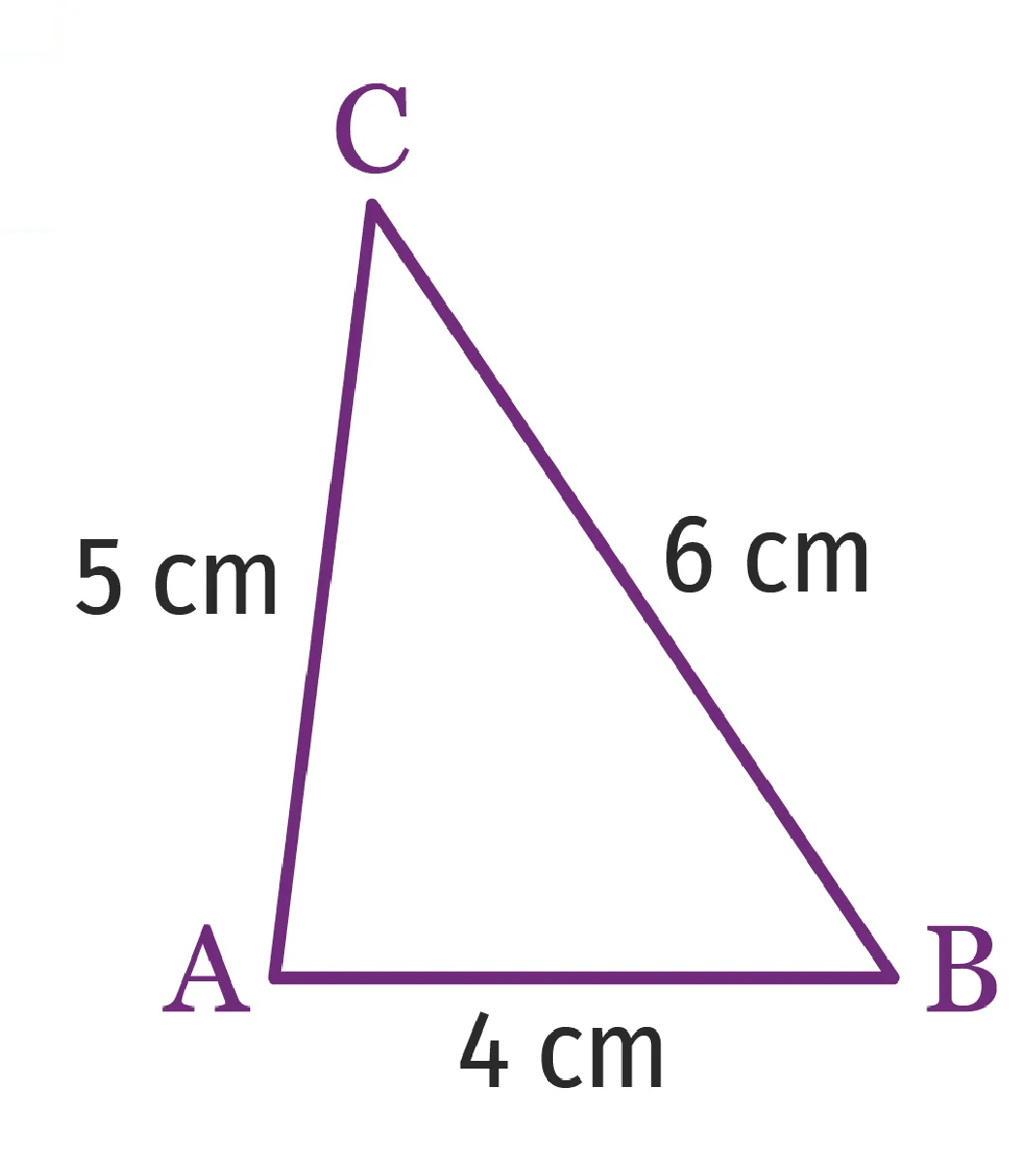
Les triangles \text{ABC} et \text{EFG} suivants sont‑ils égaux ?
1.


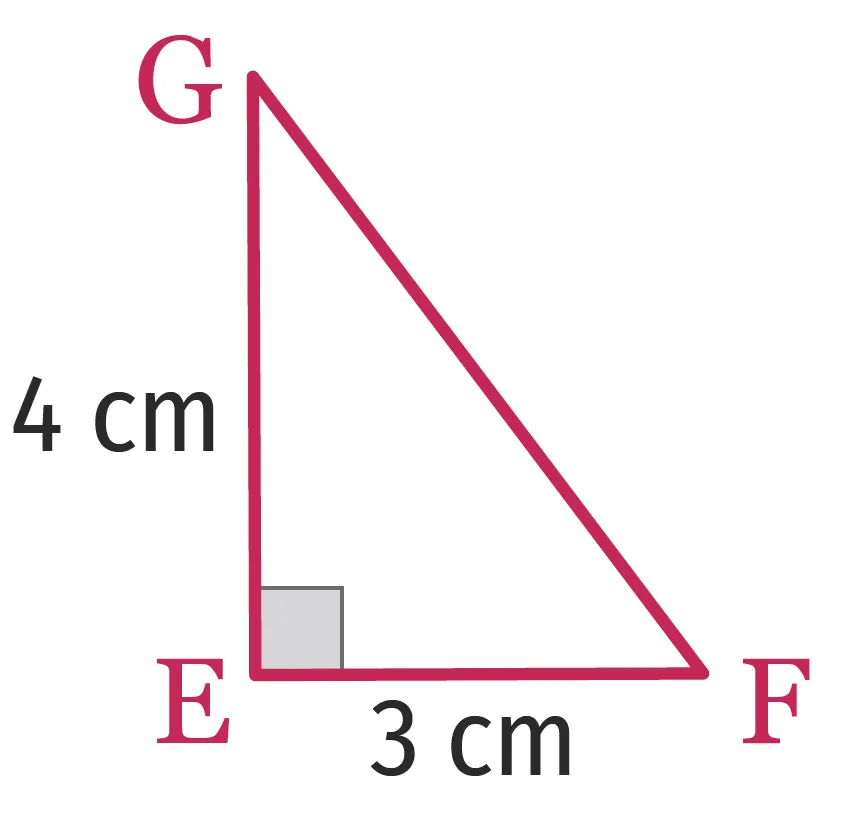
2.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouvez un à réaliser en classe pour vérifier les prérequis de ce chapitre.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
