Mathématiques Terminale Bac Pro - Cahier
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 5
Activité C
Faites du bruit !
Capacités : Résoudre algébriquement une équation du type \log(x) = a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
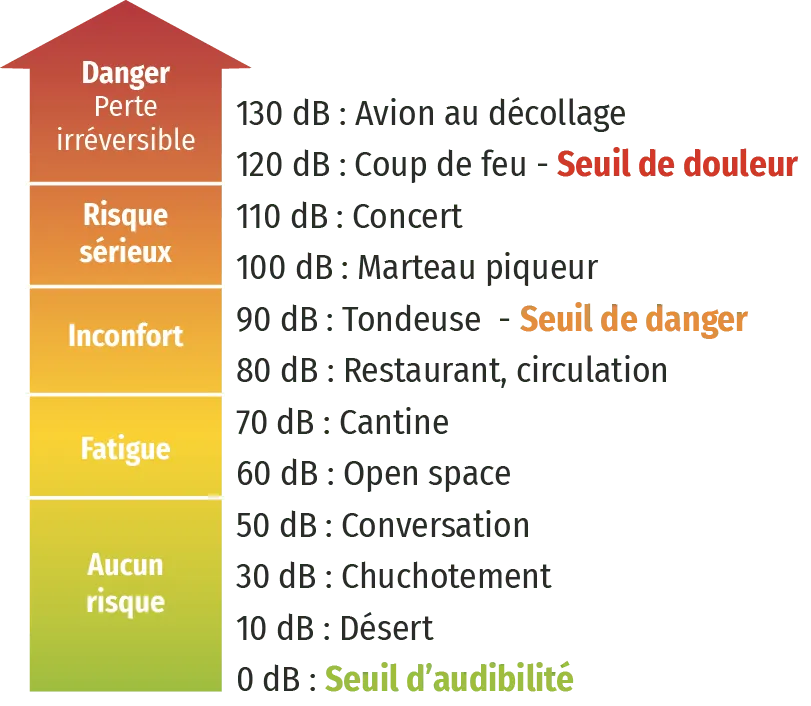
Le niveau d'intensité L d'un son en décibel (dB) est
mesuré à l'aide d'un sonomètre. Ce niveau est défini par
\mathrm{L}=10 \times \log \left(\frac{\mathrm{I}}{10^{-12}}\right), I étant l'intensité acoustique du son
mesuré, exprimée en W/m². I représente la puissance
moyenne transportée par l'onde sonore par unité de surface.
Problématique
Quelle intensité acoustique \text{I} en
W/m2 ne doit‑on pas dépasser pour ne pas entrer
dans le domaine de la douleur ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie A
Questions préparatoires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Réaliser
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Analyser/raisonner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie B
Résolution d'équation et détermination de l'intensité du seuil de douleur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Réaliser
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Réaliser
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Analyser/raisonner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
a.
S'approprier, Analyser/Raisonner
À l'aide des questions précédentes, montrer que si \mathrm{L}=10 \times \log (\mathrm{I})+120, alors \mathrm{I}=10^{\tfrac{\mathrm{L}-120}{10}}.
b. Analyser/Raisonner En déduire l'intensité acoustique \text{I} correspondant au niveau d'intensité 120 dB, correspondant au seuil de douleur.
À l'aide des questions précédentes, montrer que si \mathrm{L}=10 \times \log (\mathrm{I})+120, alors \mathrm{I}=10^{\tfrac{\mathrm{L}-120}{10}}.
b. Analyser/Raisonner En déduire l'intensité acoustique \text{I} correspondant au niveau d'intensité 120 dB, correspondant au seuil de douleur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie C
Détermination du seuil à ne pas dépasser
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
a.
Réaliser
À l'aide d'un outil numérique, tracer la courbe représentative de la fonction f définie par f(x)=10 \times \log \left(\frac{x}{10^{-12}}\right) puis la droite d'équation y = 120.
b. Analyser/raisonner D'après la Partie B, quelle est l'abscisse de leur point d'intersection ?
c. Analyser/raisonner Lire sur le graphique les solutions de l'inéquation 10 \times \log \left(\frac{\mathrm{I}}{10^{-12}}\right)>120 et répondre à la problématique .
GeoGebra
b. Analyser/raisonner D'après la Partie B, quelle est l'abscisse de leur point d'intersection ?
c. Analyser/raisonner Lire sur le graphique les solutions de l'inéquation 10 \times \log \left(\frac{\mathrm{I}}{10^{-12}}\right)>120 et répondre à la problématique .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour tout réel a, l'équation du type \log(x) = a admet pour solution .
La fonction logarithme étant, une inéquation du type \log(x) \lt a admet pour solution l'ensemble des nombres x tel que 0 \lt x \lt 10^a.
De même, une inéquation du type \log(x) > a admet pour solution l'ensemble des nombres.
La fonction logarithme étant
De même, une inéquation du type \log(x) > a admet pour solution l'ensemble des nombres
Pour s᾽entraîner :
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
