Il est conseillé de se baser sur

l'activité expérimentale 3

, p. 324 pour faire cet exercice.

1. L'équation se propageant selon l'axe Ox à une vitesse v est :
s(x, t)=A \cdot \cos (2 \pi f \cdot(t-\dfrac{x}{V})). Décrire l'onde dont l'équation est s^{\prime}(x, t)=A \cdot \cos (2 \pi f \cdot(t+\dfrac{x}{V})).

2. À l'aide du programme Python, tracer le résultat de la superposition des ondes s(x, t) et s^{\prime}(x, t). Ce type d'onde est appelé onde stationnaire. Expliquer.

Attention : la console python présente sur le site ne permet pas d'observer le déplacement de l'onde. Afin de répondre à la question, il faut recopier le code sur un ordinateur ayant une console python installée.

1. À l'aide de la calculatrice, tracer les fonctions suivantes (attention de bien spécifier les angles en radians dans les réglages de la machine) :

• f(x)=\sin ((2 \pi \times 1\,000) x) ;
• g(x)=2\sin ((2 \pi \times 1\,000) x) ;
• h(x)=\sin ((2 \pi \times 2\,000) x).

2. Calculer la fréquence de ces sinusoïdes en s'appuyant sur la période lue graphiquement. Penser à zoomer si nécessaire.

3. Comparer les courbes de f et de h, quelle est la signification physique du coefficient qui est multiplié par 2 \pi?

4. Comparer les courbes de f et de g, quel est l'effet du coefficient placé devant la fonction sinus ?

5. Tester l'effet de l'ajout d'un coefficient comme dans z(x)=\sin ((2 \pi \times 1\,000) x) en comparant sa courbe à celle de f. Quelle est la signification physique de ce coefficient et quelle serait son unité dans le cas d'une propagation d'ondes ?

Jusqu'en 1850, on pensait que l'influx nerveux, c'est-àdire la transmission d'information depuis le cerveau ou la moelle épinière jusqu'aux organes le long des fibres nerveuses appelées axones, se propageait de manière quasi instantanée. Hermann Von Helmholtz (1821-1894) fut le premier à prouver que ce n'était pas le cas, en mesurant la célérité des signaux nerveux.
Son expérience s'appuie sur un nerf de grenouille excité. Il note ainsi ses résultats : « Voici enfin les chiffres de mes expériences. La distance entre les points irrités du nerf étant de 60 millimètres, l'irritation nerveuse a mis à parcourir cet espace 0,001 4 seconde ».



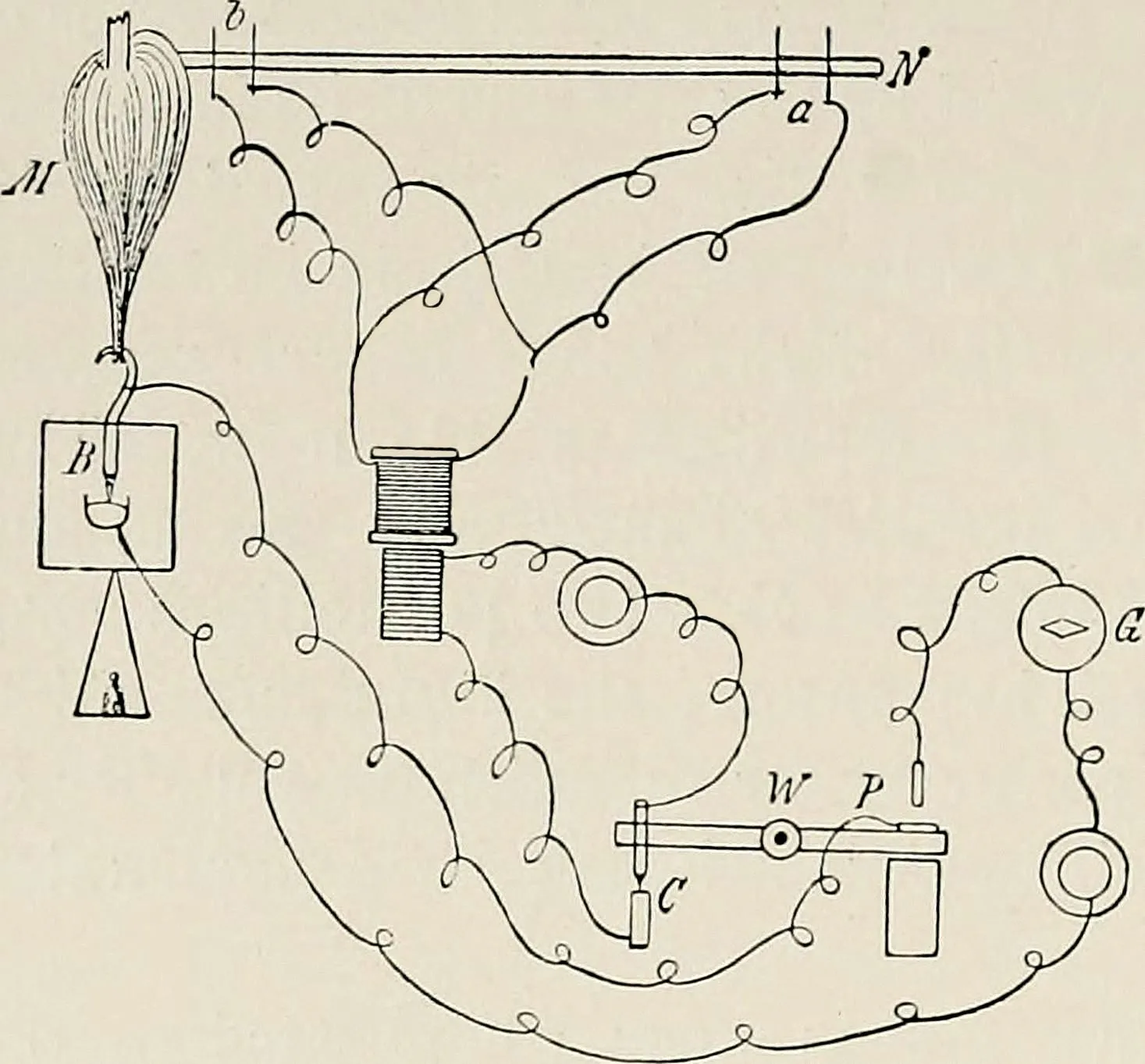
L'influx nerveux est une onde électrique : l'inversion de potentiel électrique le long du nerf (par entrée d'ions sodium \mathrm{Na}^{+} dans la fibre nerveuse appelée axone) se transmet de proche en proche.

1. Qu'est-ce qu'évoque Helmholtz quand il parle d'irritation ?

2. Quelle est la perturbation qui se propage dans le cas de l'onde nerveuse ?

3. Calculer la célérité de l'influx nerveux d'après les travaux d'Helmholtz.

4. Certains anesthésiques (lidocaïne, novocaïne, etc.) empêchent l'entrée des ions sodium. Quelle est la conséquence pour l'onde nerveuse ?

5. En déduire à quel usage peuvent être destinées ces substances en médecine ?

6. Quelle est la différence majeure entre un signal électrique se propageant dans un fil conducteur et l'influx nerveux ?

Un tube en acier vide a pour longueur L = 270 m. En attendant d'être enfoui pour servir de canalisation, il permet de réaliser des expériences scientifiques. On frappe au marteau à l'une des extrémités du tube. De l'autre côté, une personne qui colle une oreille au tube entend deux sons séparés de t = 0,75 s.

1. Expliquer pourquoi il perçoit deux sons.

2. Peut-on considérer que le décalage entre les deux sons est le retard de l'onde ? Justifier.

3. Déterminer la célérité du son dans l'acier.

• Célérité du son dans l'air : v_{\text {air}}= 340 m·s^-1.