Bientôt disponible
Ce manuel est en cours de finalisation et sera très prochainement disponible.
Couverture

Physique-Chimie 1re

Feuilleter la version papier
Chargement de l'audio en cours
Cacher

Cacher la barre d'outils

Plus

Plus

Chapitre 18


Cours




1
Le modèle ondulatoire de la lumière


A
Le rayonnement et l’onde électromagnétique

❯ Les phénomènes de diffraction et d’interférences observés lors de la propagation d’énergie lumineuse au travers d’obstacle(s) ou d’orifice(s) sont les premiers phénomènes dont l’explication fait appel à la nature ondulatoire de la lumière (doc. 1). Initiée par Christian Huygens (1678), la théorie ondulatoire n’a cessé d’être améliorée (Thomas Young, 1802 ; Augustin Fresnel, 1815). En 1865, James Maxwell finalise le modèle et prédit l’existence et la célérité de l’onde électromagnétique.

Une onde électromagnétique (OEM) :
  • est un phénomène vibratoire qui se propage dans le vide et de nombreux milieux (transparents ou non) ;
  • est constituée d’un champ électrique et d’un champ magnétique oscillants, orthogonaux entre eux, et orthogonaux à la direction de propagation ;
  • se propage dans le vide à la célérité c=3,00×108c=3\text{,}00 \times 10^{8} m·s-1.

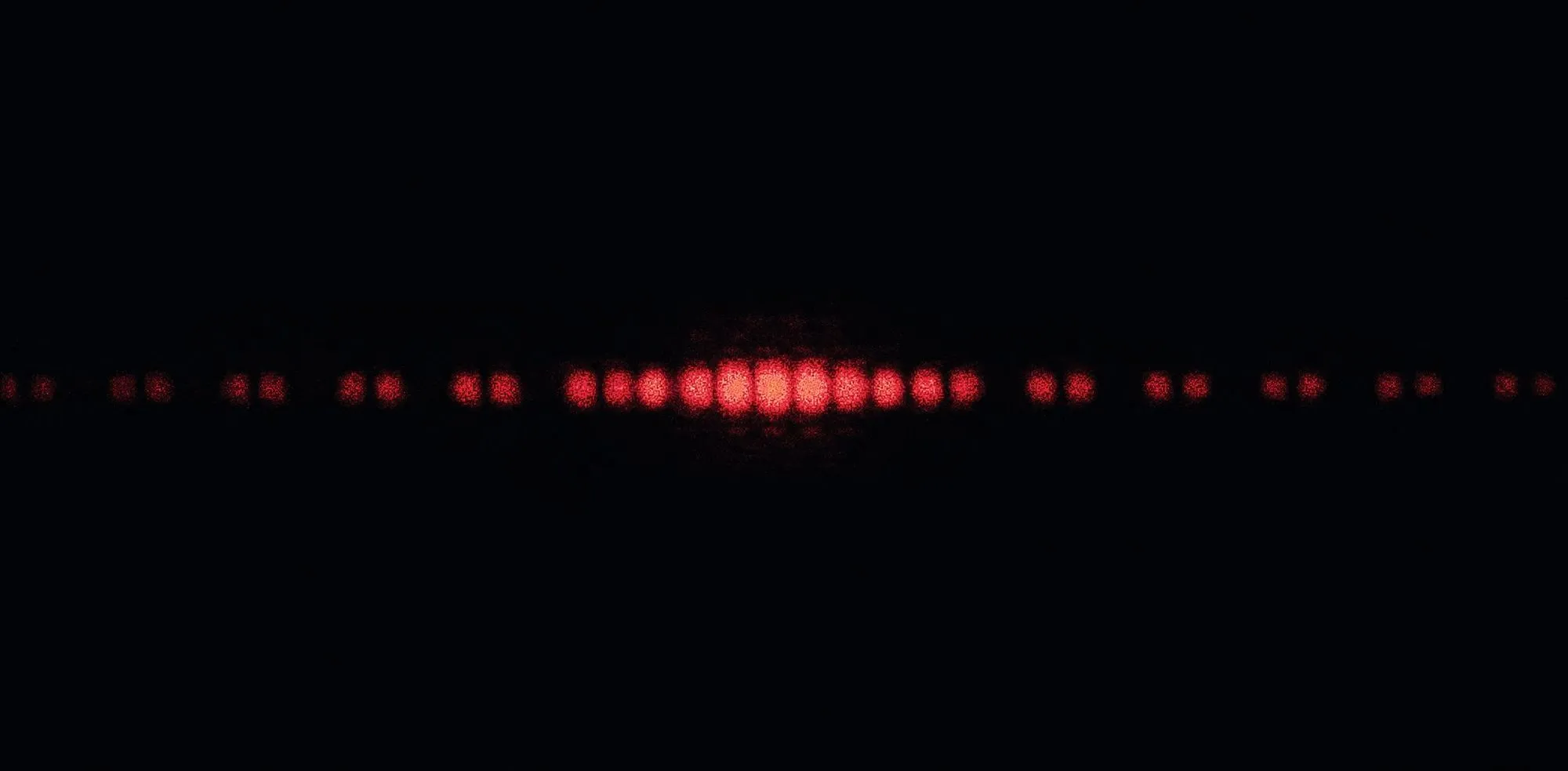
Doc. 1
Observations expérimentales

a) Figure de diffraction d’un faisceau laser par une fente simple.

Figure de diffraction d’un faisceau laser par une fente simple


b) Figure d’interférence d’un faisceau laser par une double fente.

Figure d’interférence d’un faisceau laser par une double fente

B
Les caractéristiques d’une OEM

❯ Une onde électromagnétique monochromatique est caractérisée par :
  • sa longueur d’onde, notée λ\lambda (lambda), qui correspond à sa période spatiale. Elle s'exprime en mètre (m) (doc. 2) ;
  • sa fréquence, notée ν\nu (nu) ou ff, correspond à l’inverse de la période temporelle T.T. Elle s’exprime en hertz (Hz).
La longueur d’onde λ\lambda et la fréquence ν\nu sont reliées dans le vide par l’expression : λ=cν.\lambda=\dfrac{c}{\nu}.

Doc. 2
Représentation d’une OEM

Représentation d’une OEM

C
Le spectre électromagnétique

❯ Chaque être vivant s’approprie le monde dans lequel il vit à l’aide de ses sens, en particulier la vue. Cependant, l’être humain a pris conscience que les informations qu’il perçoit visuellement de son environnement peuvent être limitées.

❯ Le domaine visible (400400 nm <λ<\lt\lambda\lt 800800 nm) n’est qu’une infime partie des ondes électromagnétiques.

À l’aide de la longueur d’onde ou de la fréquence, on classe le spectre électromagnétique en sept sous-domaines principaux selon leur découverte ou leur utilisation. Dans l’ordre croissant des longueurs d’onde, on rencontre : les rayons γ\gamma, les rayons X\text{X}, les ultraviolets, le visible, les infrarouges (proches et lointains), les micro-ondes et les ondes radio (voir doc. 3).

Supplément numérique

Qu’est-ce qu’une onde électromagnétique ? Retrouvez toutes les informations en vidéo.

Vocabulaire

  • Fréquence : nombre de périodes ou de vibrations par seconde.
  • Longueur d’onde : distance λ\lambda parcourue par l’onde pendant la durée d’une période T.T.

Éviter les erreurs

➜ La fréquence ne dépend pas du milieu de propagation contrairement à la longueur d’onde.
➜ Aucun objet matériel connu ne peut se déplacer plus rapidement que la lumière.

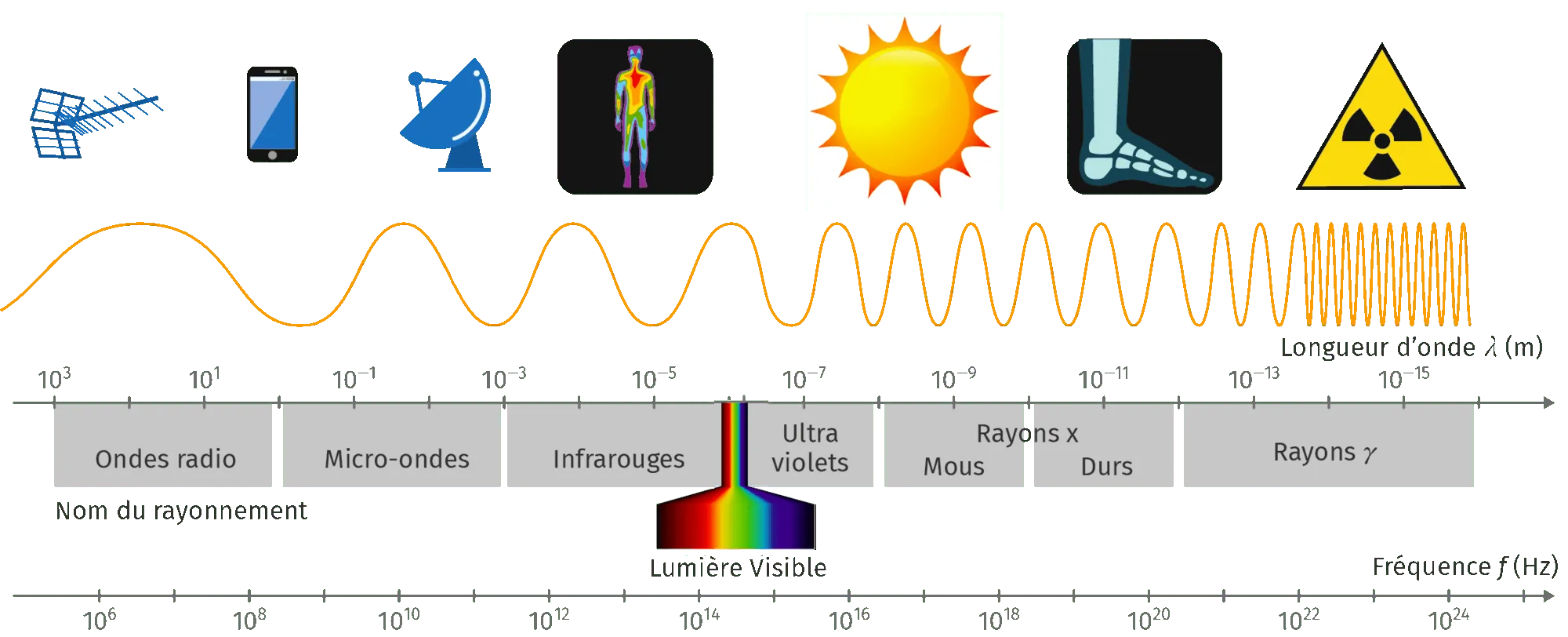
Doc. 3
Le spectre électromagnétique simplifié

Le spectre électromagnétique simplifié

2
Le modèle particulaire de la lumière


A
L’imperfection du modèle ondulatoire

❯ Bien que les lois de l’électromagnétisme formulées par Maxwell au cours du XIXe siècle expliquent de nombreuses observations expérimentales, elles ne permettent pas d’interpréter le rayonnement émis par des corps chauffés et l’effet photoélectrique.

Le modèle ondulatoire explique la propagation de la lumière (OEM) et la formation des images mais est inopérant pour expliquer les interactions d’énergies avec la matière.


Pas de malentendu

➜ Les modèles ondulatoire et particulaire de la lumière modélisent les différentes manifestations de l’interaction de cette dernière avec son environnement.

➜ L’existence simultanée des deux modèles, à première vue contradictoires, illustre la dualité onde-corpuscule de la lumière.

B
Le photon et son énergie

❯ Afin de modéliser les interactions entre la matière et le rayonnement en coïncidence avec l’observation d’un corps noir, Planck propose en 1900 de quantifier l’énergie de l’onde à l’aide d’un paquet d’énergie indivisible : le quantum. Tout échange d’énergie avec la matière est un multiple entier de ce minimum d’énergie : la théorie des quanta est née.
  • Pour expliquer l’effet photoélectrique, Einstein associe en 1905 cette idée de quantum à une structure particulaire de la lumière, le photon.
  • Chaque rayonnement est par conséquent constitué d’un nombre entier de photons possédant chacun une énergie minimale égale au quantum d’énergie Ephoton=h⋅ν.E_{\text {photon}}=h \cdot \nu.
    EphotonE_{\text {photon}} s’exprime en joule (J) et la fréquence ν\nu en hertz (Hz). hh est la constante de Planck : h=6,63×10−34h=6\text{,}63 \times 10^{-34} J·s.
  • Le photon est une particule de masse et de charge électrique nulles se déplaçant, dans le vide, à la vitesse de la lumière.

Remarque : L’énergie d’un photon est d’autant plus grande que sa fréquence est élevée (et que sa longueur d’onde est faible).

Doc. 4
L’effet photoélectrique

Il s’agit de l’émission d’un courant électrique par un métal en présence de lumière. La vitesse des électrons arrachés ne dépend pas du flux lumineux mais uniquement de la longueur d’onde.

Vocabulaire

  • Corpuscule : synonyme de particule.
  • Radiation : déplacement de photons.
  • Quantum : mot latin signifiant la plus petite quantité d’énergie indivisible transportée par une radiation. Le centime est à la monnaie ce que le quantum est à la quantité d’énergie d’un atome.
  • Photon : particule élémentaire qui transporte le quantum d’énergie lumineuse.

Données

  • h=6,63×10−34h=6\text{,}63 \times 10^{-34} J·s ;
  • 11 eV =1,60×10−19=1\text{,}60 \times 10^{-19} J ;
  • c=3,00×108c=3\text{,}00 \times 10^{8} m·s-1.

Application

Calculer l’énergie du photon le plus énergétique du domaine visible.

Corrigé :
  • Avec un domaine visible compris entre 400400 nm et 800800 nm, la radiation la plus énergétique est celle de plus courte longueur d’onde, soit 400400 nm (à la limite de l’UV).
  • On peut déterminer successivement la fréquence de la radiation ν=cλ\nu=\dfrac{c}{\lambda} puis l’énergie EE égale à E=h⋅νE=h \cdot \nu soit directement E=h⋅cλ.E=\dfrac{h \cdot c}{\lambda}.
  • Numériquement E=6,63×10−34×3,00×108400×10−9E=\dfrac{6\text{,}63 \times 10^{-34} \times 3\text{,}00 \times 10^{8}}{400 \times 10^{-9}} donc E=4,97×10−19E=4\text{,}97 \times 10^{-19} J soit E=3,11E=3\text{,}11 eV.

Éviter les erreurs

➜ L’énergie d’un photon est toujours positive :
Ephoton>0.E_{\text {photon}}>0.

➜ L’unité légale de l’énergie est le joule. Cependant, les énergies échangées lors des interactions entre la lumière et la matière sont si faibles qu’on utilise le plus souvent l’électron-volt (eV) :
11 eV =1,60×10−19=1\text{,}60 \times 10^{-19} J.

3
La quantification des niveaux d’énergie d’un atome


A
Le diagramme d’énergie d’un atome

❯ Chaque atome possède une structure électronique de couches et sous-couches (1s, 2s, 2p, etc.) sur lesquelles se répartissent tous les électrons. Ces couches existent même si elles ne sont pas occupées.
Chaque sous-couche associée à une orbite possède sa propre énergie, qui est d’autant plus faible qu’elle est proche du noyau.

On utilise un diagramme énergétique pour représenter les différents niveaux d’énergie intrinsèques à l’atome.

Chaque niveau d'énergie est modélisé par une ligne horizontale. On reporte leur valeur d'énergie sur un axe vertical, le plus souvent exprimé en électron-volt (eV).
L’énergie de l’atome correspond à la somme des énergies de chaque électron. À chaque niveau correspond un état.

❯ On distingue deux types d’états : l’état fondamental, souvent noté E1E_{1}, et les états supérieurs, dits excités. L’état ionisé étant l’état (limite) pour lequel l’électron a quitté l’atome (doc. 5). L'état ionisé correspond au niveau d'énergie E∞=0E_{\infty}=0 eV, tous les autres niveaux ont une énergie négative.

D’après Niels Bohr (1913), l’atome n’est stable que pour certaines valeurs d’énergie discrètes bien définies. Son énergie est quantifiée.

Éviter les erreurs

➜ Attention à la conversion entre le joule (J) et l’électron- volt (eV).

Doc. 5
L’effet photoélectrique

L’effet photoélectrique

B
L’émission et l’absorption d’un photon

❯ Lors d’une transition entre deux niveaux d’énergie, notés EnE_{\mathrm{n}} et EmE_{\mathrm{m}} :
  • l'énergie d'un atome augmente ou diminue, respectivement en absorbant ou en émettant un photon ;
  • l’énergie échangée ∣ΔE∣|\Delta E| (absorbée/émise) par l’atome possède exactement une valeur égale à la différence des niveaux d’énergie ∣ΔEatome∣=∣En−Em∣|\Delta E_{\text {atome}}|=|E_{\mathrm{n}}-E_{\mathrm{m}}| ;
  • la variation d’énergie de l’atome est égale à l’énergie d’un photon.

Vocabulaire

  • Transition : passage d’un électron d’un niveau d’énergie à un autre. Elle est représentée par une flèche.
  • État fondamental : état stable de plus faible énergie de l’atome.

Éviter les erreurs

➜ Lors d’une transition, un photon ne peut être absorbé ou émis par l’atome que si : Ephoton=∣ΔEatome∣.E_{\text {photon}}=|\Delta E_{\text {atome}}|.
➜ Une variation ΔE<0\Delta E\lt0 correspond à l'émission d'un photon, ΔE>0\Delta E>0 une absorption d'un photon.
page 364
page 368
Connectez-vous pour ajouter des favoris

Pour pouvoir ajouter ou retrouver des favoris, nous devons les lier à votre compte.Et c’est gratuit !

Livre du professeur

Pour pouvoir consulter le livre du professeur, vous devez être connecté avec un compte professeur et avoir validé votre adresse email académique.

Votre avis nous intéresse !
Recommanderiez-vous notre site web à un(e) collègue ?

Peu probable
Très probable

Cliquez sur le score que vous voulez donner.

Dites-nous qui vous êtes !

Pour assurer la meilleure qualité de service, nous avons besoin de vous connaître !
Cliquez sur l'un des choix ci-dessus qui vous correspond le mieux.

Nous envoyer un message




Nous contacter?

Votre fiche établissement

Renseigner ce formulaire vous permettra d'ajouter votre établissement.