Physique-Chimie 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
1. Constitution et transformations de la matière
Ch. 1
Composition chimique d'un système
Ch. 2
Composition chimique des solutions
Ch. 3
Évolution d'un système chimique
Ch. 4
Réactions d'oxydoréduction
Ch. 5
Détermination d'une quantité de matière par titrage
Livret Bac : Thème 1
Ch. 6
De la structure à la polarité d'une entité
Ch. 7
Interpréter les propriétés d’une espèce chimique
Ch. 8
Structure des entités organiques
Ch. 9
Synthèse d'espèces chimiques organiques
Ch. 10
Conversions d'énergie au cours d'une combustion
Livret Bac : Thème 1 bis
2. Mouvement et interactions
Ch. 11
Modélisation d'interactions fondamentales
Ch. 12
Description d'un fluide au repos
Ch. 13
Mouvement d'un système
Livret Bac : Thème 2
3. L'énergie, conversions et transferts
Ch. 14
Études énergétiques en électricité
Ch. 15
Études énergétiques en mécanique
Livret Bac : Thème 3
4. Ondes et signaux
Ch. 16
Ondes mécaniques
Ch. 17
Images et couleurs
Ch. 18
Modèles ondulatoire et particulaire de la lumière
Livret Bac : Thème 4
Méthode
Fiches méthode
Fiche méthode compétences
Annexes
Thème 2
Sujet bac 3
Tir parabolique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1 Aux origines du mouvement
Depuis très longtemps, on a cherché à comprendre les mouvements que l'on observait, que ce soit ceux des astres ou bien des objets qui nous entourent.
Aristote a défini deux types de mouvements :
Durant le Moyen Âge, un nouveau concept est introduit, l'impetus. Lorsqu'un objet est mis en mouvement, il reçoit de l'impetus et c'est cet impetus qui lui permet de maintenir son mouvement.


Au XVIIe siècle, Galilée introduit la notion d'inertie : un corps persévère naturellement dans son mouvement rectiligne uniforme, sauf s'il subit une contrainte qui l'en déviera. Ainsi un objet envoyé en l'air continuerait son mouvement en ligne droite à la même vitesse, s'il ne subissait pas une contrainte qui modifiait sa trajectoire.
Aristote a défini deux types de mouvements :
- les mouvements naturels où les objets cherchent à retourner à leur place propre ;
- les mouvements violents qui sont des mouvements forcés, où les objets s'éloignent de leur place propre.
Durant le Moyen Âge, un nouveau concept est introduit, l'impetus. Lorsqu'un objet est mis en mouvement, il reçoit de l'impetus et c'est cet impetus qui lui permet de maintenir son mouvement.


Au XVIIe siècle, Galilée introduit la notion d'inertie : un corps persévère naturellement dans son mouvement rectiligne uniforme, sauf s'il subit une contrainte qui l'en déviera. Ainsi un objet envoyé en l'air continuerait son mouvement en ligne droite à la même vitesse, s'il ne subissait pas une contrainte qui modifiait sa trajectoire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2 Le tir à l'arc
Lors de l'épreuve olympique de tir à l'arc en extérieur, les tireurs doivent atteindre une cible qui se trouve à 70 mètres. Lors de ce lancer, la trajectoire de la flèche est parabolique, elle dépend de l'angle avec lequel la flèche est tirée, ainsi que de sa vitesse de lancement.

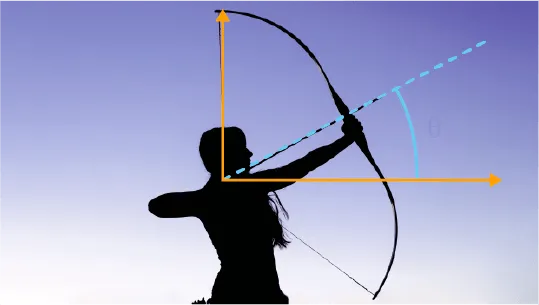
La distance maximale parcourue par la flèche est appelée portée. Si on néglige les frottements de l'air et que l'on prend pour origine du repère la position initiale de la flèche, on peut calculer cette distance à l'aide de la relation :
avec v la vitesse de lancer de la flèche et g l'intensité de la pesanteur terrestre.


La distance maximale parcourue par la flèche est appelée portée. Si on néglige les frottements de l'air et que l'on prend pour origine du repère la position initiale de la flèche, on peut calculer cette distance à l'aide de la relation :
\text{D} = \dfrac{v^2}{g} \:· \:\text{sin}(2 \theta)
avec v la vitesse de lancer de la flèche et g l'intensité de la pesanteur terrestre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- m_{\text{Lune}} = 7,3477 \times 1022 kg ;
- R_{\text{Lune}} = 1 737 km ;
- G = 6,67 \times 10-11 N·m2·kg-2 ;
- g = 9,81 N·kg-1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
1. Pour Aristote l'endroit naturel des objets solides est le sol. Interpréter alors le mouvement de la flèche d'après la théorie d'Aristote.
2. D'après le modèle établi par Galilée, quel devrait être le mouvement de la flèche une fois lancée si elle ne subissait aucune action ?
3. Identifier l'action exercée sur la flèche expliquant son mouvement parabolique.
Une flèche est lancée à une vitesse de 300 km·h-1 avec un angle de 5° par rapport à l'horizontale.
4. Calculer la distance D_1 qu'elle va parcourir.
5. Exprimer \theta à partir de la relation donnée dans le doc. 2.
2. D'après le modèle établi par Galilée, quel devrait être le mouvement de la flèche une fois lancée si elle ne subissait aucune action ?
3. Identifier l'action exercée sur la flèche expliquant son mouvement parabolique.
Une flèche est lancée à une vitesse de 300 km·h-1 avec un angle de 5° par rapport à l'horizontale.
4. Calculer la distance D_1 qu'elle va parcourir.
5. Exprimer \theta à partir de la relation donnée dans le doc. 2.
Une nouvelle flèche est également lancée à 300 km·h-1 et parcourt une distance de D_2 = 70 m.
6. Calculer l'angle d'inclinaison avec lequel elle a été envoyée.
L'intensité de pesanteur g_\text{{astre}} à la surface d'un astre est liée à sa masse m et à son rayon R par la relation : g_{\text{astre}} = G \: · \: \dfrac{m}{R^2}.
7. Calculer g_{\text{Lune}} avec les chiffres significatifs appropriés.
On imagine maintenant que le tireur est sur la Lune et lance sa flèche avec les mêmes conditions initiales qu'à la question 4., la flèche parcourt une distance D_{\text{Lune}}.
8. Déterminer la relation entre les grandeurs g, g_{\text{Lune}}, D_{1} et D_{\text{Lune}}. Calculer la valeur de la distance D_{\text{Lune}}.
6. Calculer l'angle d'inclinaison avec lequel elle a été envoyée.
L'intensité de pesanteur g_\text{{astre}} à la surface d'un astre est liée à sa masse m et à son rayon R par la relation : g_{\text{astre}} = G \: · \: \dfrac{m}{R^2}.
7. Calculer g_{\text{Lune}} avec les chiffres significatifs appropriés.
On imagine maintenant que le tireur est sur la Lune et lance sa flèche avec les mêmes conditions initiales qu'à la question 4., la flèche parcourt une distance D_{\text{Lune}}.
8. Déterminer la relation entre les grandeurs g, g_{\text{Lune}}, D_{1} et D_{\text{Lune}}. Calculer la valeur de la distance D_{\text{Lune}}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
