Chapitre 9
TP INFO 1
Coordonnées dépendant du temps
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On se place dans un repère orthonormé. Pour tout instant t \geqslant 0 exprimé en minute, un objet représenté par le point \text{M} est localisé par son abscisse x(t)=\cos (t) et son ordonnée y(t)=\sin (2 t), toutes deux exprimées en mètre. On cherche à tracer la courbe décrite par \text{M} dans ce repère.
Question préliminaire :
Montrer qu'aux instants t et t + 2\pi, le point \text{M} a les mêmes coordonnées.
Montrer qu'aux instants t et t + 2\pi, le point \text{M} a les mêmes coordonnées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Tracer la courbe décrite par \mathbf{M} et observer des propriétés graphiques en utilisant une des trois méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce type de courbe est appelée courbe paramétrique et sera étudiée après la terminale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
1. On propose ici de représenter à l'aide du tableur l'ensemble des points obtenus pour des valeurs de t variant de 0 à 2\pi, avec un pas de h.
a. Reproduire et compléter la feuille de calcul ci‑dessous. (Fichier téléchargeable .)
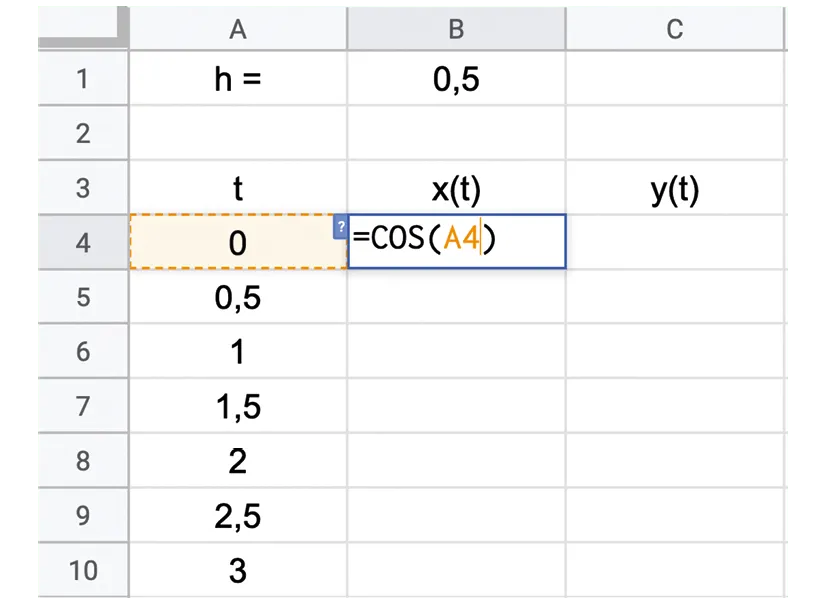
a. Reproduire et compléter la feuille de calcul ci‑dessous. (Fichier téléchargeable .)
b. À l'aide de l'outil graphique, en sélectionnant les colonnes B et C, créer un nuage de points de coordonnées (x(t) ; y(t)).
c. Adapter cette méthode avec un pas de h égal à 0{,}2, puis à 0{,}1.
2. Quelle propriété retrouve‑t‑on lorsque le compteur t varie de 0 à 2\pi ?
c. Adapter cette méthode avec un pas de h égal à 0{,}2, puis à 0{,}1.
2. Quelle propriété retrouve‑t‑on lorsque le compteur t varie de 0 à 2\pi ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2GeoGebra
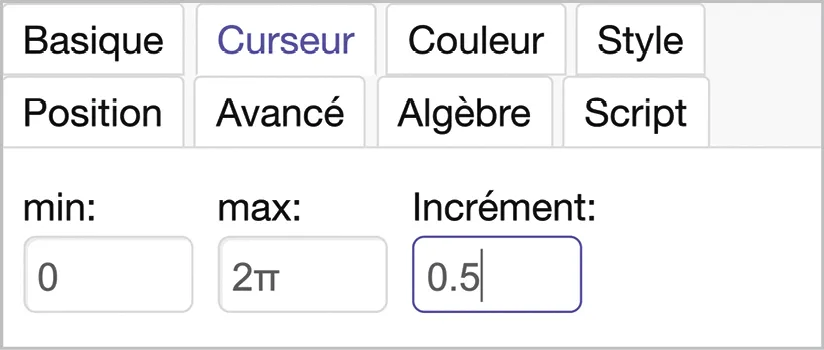
1. Créer un curseur t allant de 0 à 2\pi, avec un incrément de 0{,}5.
2. Dans le champ Saisie, créer le point \mathrm{M} :
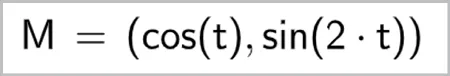
3. a. Activer la trace de \text{M} et déplacer le curseur pour observer la courbe décrite par \text{M}.
b. Recommencer avec un incrément de 0{,}2 puis de 0{,}1.
4. Quelle propriété retrouve‑t‑on lorsque le curseur varie de 0 à 2\pi ?
5. Retrouver le profil de la courbe directement à l'aide de la saisie d'une courbe dite « paramétrée » :
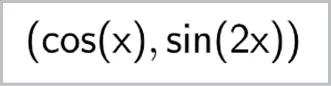
2. Dans le champ Saisie, créer le point \mathrm{M} :
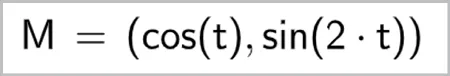
3. a. Activer la trace de \text{M} et déplacer le curseur pour observer la courbe décrite par \text{M}.
b. Recommencer avec un incrément de 0{,}2 puis de 0{,}1.
4. Quelle propriété retrouve‑t‑on lorsque le curseur varie de 0 à 2\pi ?
5. Retrouver le profil de la courbe directement à l'aide de la saisie d'une courbe dite « paramétrée » :
GeoGebra
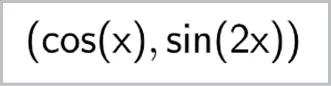
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 3Calculatrice
1. Démontrer algébriquement que y(t)=2 x(t) \sqrt{1-x^{2}(t)} ou y(t)=-2 x(t) \sqrt{1-x^{2}(t)}.
2. Tracer les courbes des deux fonctions obtenues à la question 1.
2. Tracer les courbes des deux fonctions obtenues à la question 1.
GeoGebra
3. Quelles propriétés graphiques observe‑t‑on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Montrer que si \mathrm{M}(a~; b) est un point de la courbe, alors il en est de même pour les points \mathrm{A}(a~;-b) ; \mathrm{B}(-a~; b) et \mathrm{C}(-a~;-b). Quelles conséquences peut on tirer de cette remarque ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
